Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

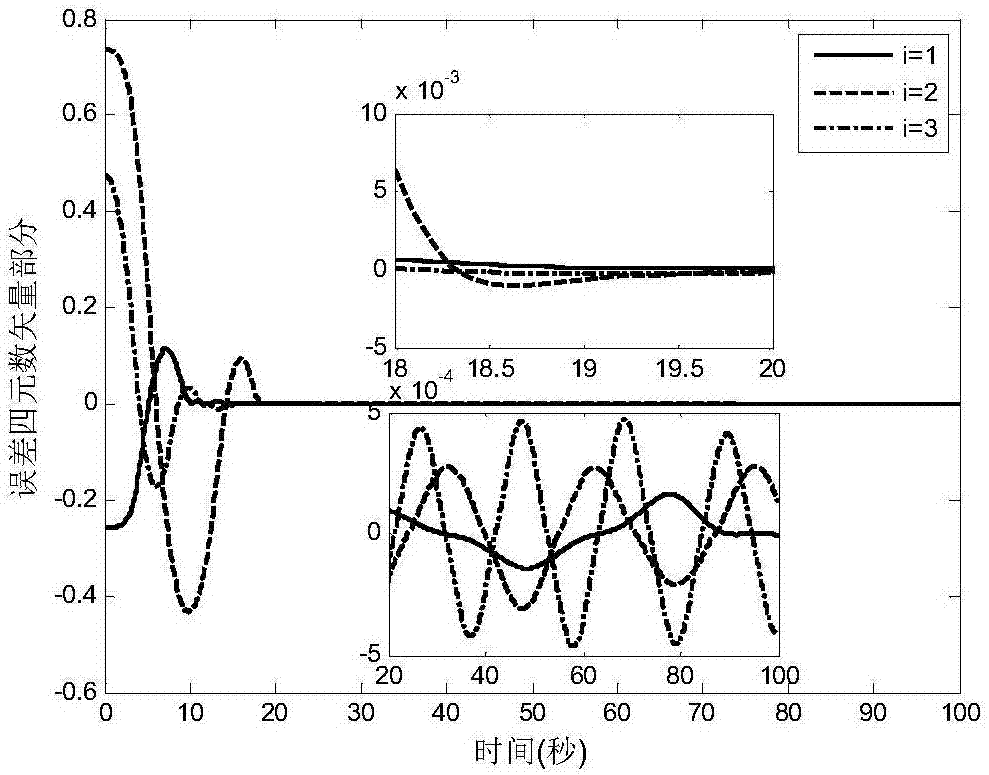
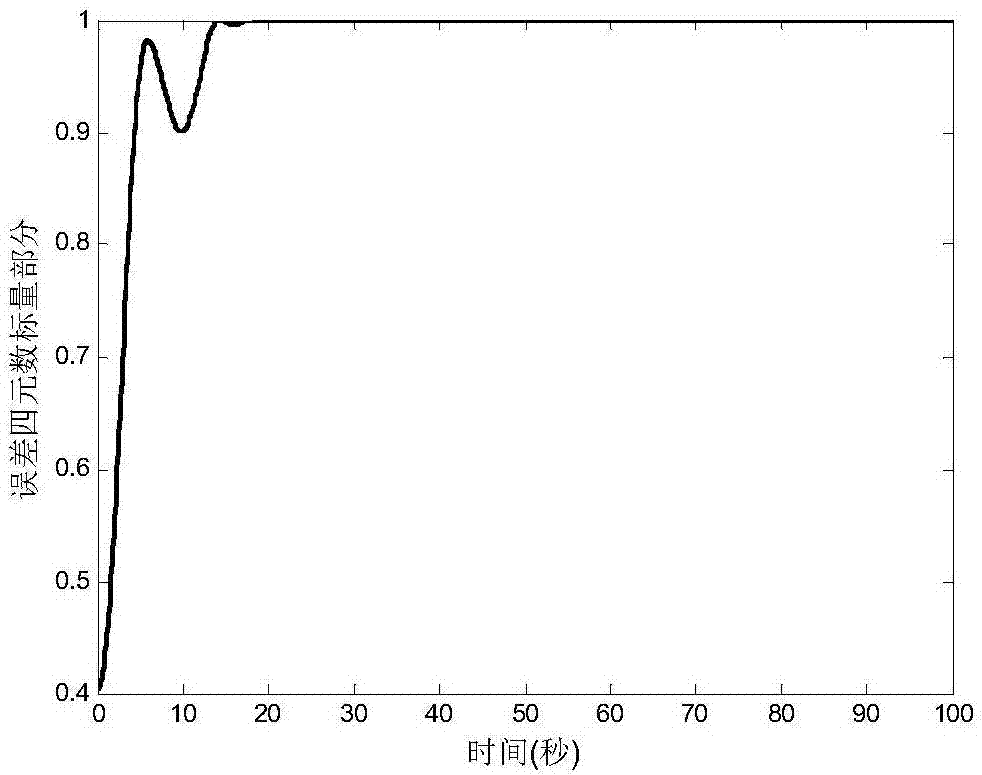
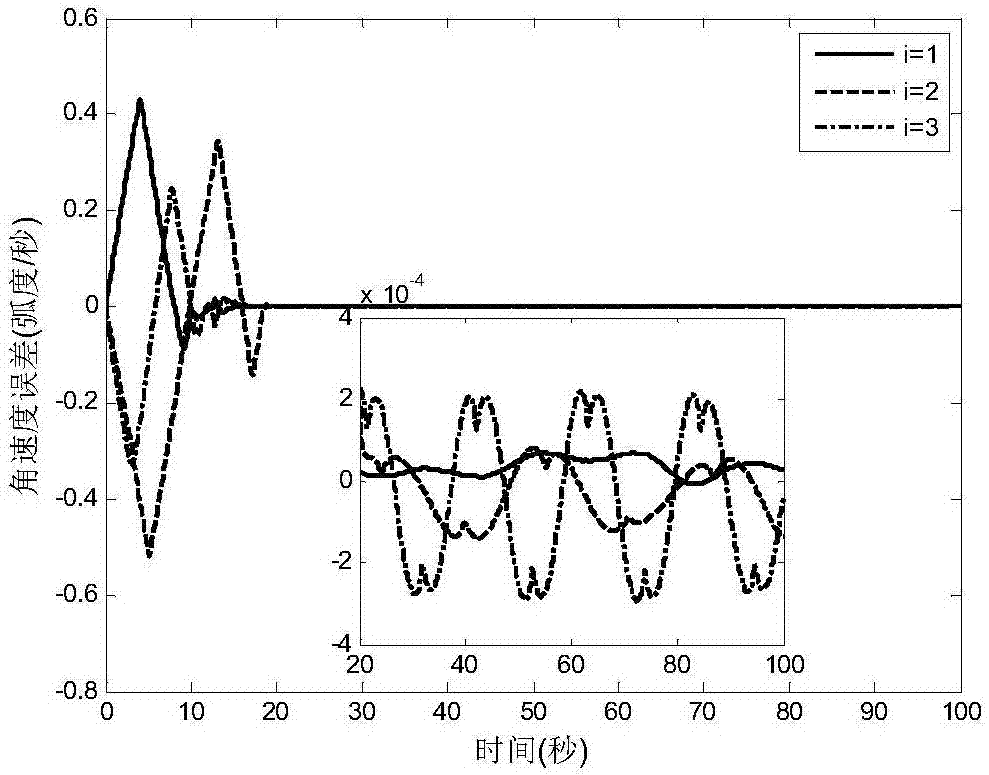
Spacecraft robust finite time saturation attitude tracking control method

A limited-time, tracking control technology, applied in adaptive control, general control system, control/regulation system, etc., can solve the problems of limited application scope of control algorithm, complex controller structure, uncertain model, etc., and achieve control parameters. The tuning process is simple, the convergence speed is accelerated, and the applicability is enhanced.

Active Publication Date: 2017-06-23
HARBIN INST OF TECH
View PDF3 Cites 40 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0006] The purpose of the present invention is to solve the problem of rigid body spacecraft attitude tracking control under the conditions of model uncertainty, external disturbance torque and actuator saturation, etc., and aim at the controller chattering, controller structure complexity, Due to the problems of many tuning parameters and limited application range of the control algorithm, a robust finite-time saturated attitude tracking control method for spacecraft is proposed

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Spacecraft robust finite time saturation attitude tracking control method
  • Spacecraft robust finite time saturation attitude tracking control method
  • Spacecraft robust finite time saturation attitude tracking control method

Examples

Experimental program
Comparison scheme
Effect test

specific Embodiment approach 1

[0038] Specific implementation mode one: a spacecraft robust finite-time saturation attitude tracking control method in this implementation mode includes the following steps:

[0039] Step 1: Establish the attitude kinematics and dynamics model of the rigid body spacecraft, that is, the attitude tracking system;

[0040] Step 2: Define fast non-singular terminal sliding surface and auxiliary system according to Step 1;

[0041] Step 3: Design a robust finite-time saturation attitude tracking controller;

[0042] When the upper bound of the integrated uncertainty δ of the attitude tracking system is an unknown constant, a robust finite-time saturated attitude tracking controller is designed according to the fast non-singular terminal sliding mode surface obtained in step 2 and the auxiliary system;

[0043] When the upper bound of the comprehensive uncertainty δ of the attitude tracking system is an unknown function, an adaptive robust finite-time saturated attitude tracking c...

specific Embodiment approach 2

[0044] Specific embodiment two: the difference between this embodiment and specific embodiment one is: the specific process of establishing the attitude kinematics and dynamics model of the rigid body spacecraft in the step one is:

[0045] Select the quaternion as the parameter describing the attitude of the spacecraft, and establish the kinematics model and dynamics model of the system as described in formula (1) and formula (2):

[0046]

[0047]

[0048]

[0049] and Respectively represent the spacecraft body coordinate system E b with the desired coordinate system E d Between the relative quaternion and the relative angular velocity, the calculation rules are as follows:

[0050]

[0051]

[0052] in, Indicates the spacecraft body coordinate system E b Relative to the geocentric inertial coordinate system E n attitude, q 0 and q v satisfy constraints Represents a quaternion multiplication operation; Denotes the desired coordinate system E ...

specific Embodiment approach 3

[0067] Specific embodiment three: the difference between this embodiment and specific embodiment one or two is: the specific process of defining the fast non-singular terminal sliding mode surface and the auxiliary system according to step one in said step two is:

[0068] In order to facilitate the design of the controller and the analysis of the stability of the system, this section first gives the definition of the fast non-singular terminal sliding mode surface, the definition of the auxiliary system and related lemmas.

[0069]In order to ensure that the system state on the sliding surface has a fast convergence rate and the controller has no singularity, the fast non-singular terminal sliding surface (FNTSMS) is constructed as follows:

[0070]

[0071] in,

[0072]

[0073]

[0074] r 1 =(2-γ)η γ-1 ,r 2 =(γ-1)η γ-2 ,0<γ,η<1 (15)

[0075]

[0076]

[0077] Among them, i=1,2,3 means relative quaternion medium vector part The subscripts of each elem...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

A spacecraft robust finite time saturation attitude tracking control method is disclosed. The present invention relates to the spacecraft robust finite time saturation attitude tracking control method so as to solve a rigid spacecraft attitude tracking control problem in the conditions of model uncertainties, external disturbance torques and actuator saturation and is aimed at the problems of controller chattering, a complex controller structure, many setting parameters and a limited application range of a control algorithm in an existing method. The method of the invention comprises the steps of (1) establishing a rigid spacecraft attitude kinematics and dynamics model which is an attitude tracking system, (2) defining a rapid nonsingular terminal sliding mode surface and auxiliary system according to the step (1), and (3) carrying out robust finite time saturation attitude tracking controller design, carrying out controller designing when the synthetical uncertainty delta upper bound of the attitude tracking system is an unknown constant, and carrying out adaptive controller designing when the synthetical uncertainty delta upper bound is an unknown function. The spacecraft robust finite time saturation attitude tracking control method is used for the aerospace field.

Description

technical field [0001] The invention relates to a spacecraft robust finite-time saturation attitude tracking control method. Background technique [0002] With the improvement of space research and application capabilities, the demand for on-orbit service technology is becoming increasingly urgent. The major aerospace countries have realized its importance, and have carried out corresponding research on the future on-orbit service system. These studies can be used to remove orbital debris, on-orbit maintenance and other tasks. On-orbit service includes five key technologies: measurement technology for space non-cooperative targets, approaching docking technology, capture mechanism technology, contact collision dynamics modeling technology during capture, and joint stabilization technology after capture. Among them, the attitude control technology for the assembly formed after the capture is completed plays a very important role in the successful implementation of the on-orb...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): G05B13/04
Inventor 宋申民陈海涛李学辉武冠群
Owner HARBIN INST OF TECH
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com