Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

A time-varying convex quadratic programming solver design method

A technique of convex quadratic programming and quadratic programming, which is applied in the field of time-varying quadratic programming problem solvers in the real number domain, and can solve problems such as unreasonable and difficult to satisfy

Active Publication Date: 2020-08-18
SOUTH CHINA UNIV OF TECH
View PDF4 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

When the neural network is applied in the actual system, such a requirement is sometimes difficult to meet
In addition, in the actual system, the reciprocal of the inductance parameter value and the capacitance parameter value is usually time-varying, especially in large-scale power electronic systems, AC motor control systems, power network systems, etc., the system parameters are set to fixed values is unreasonable

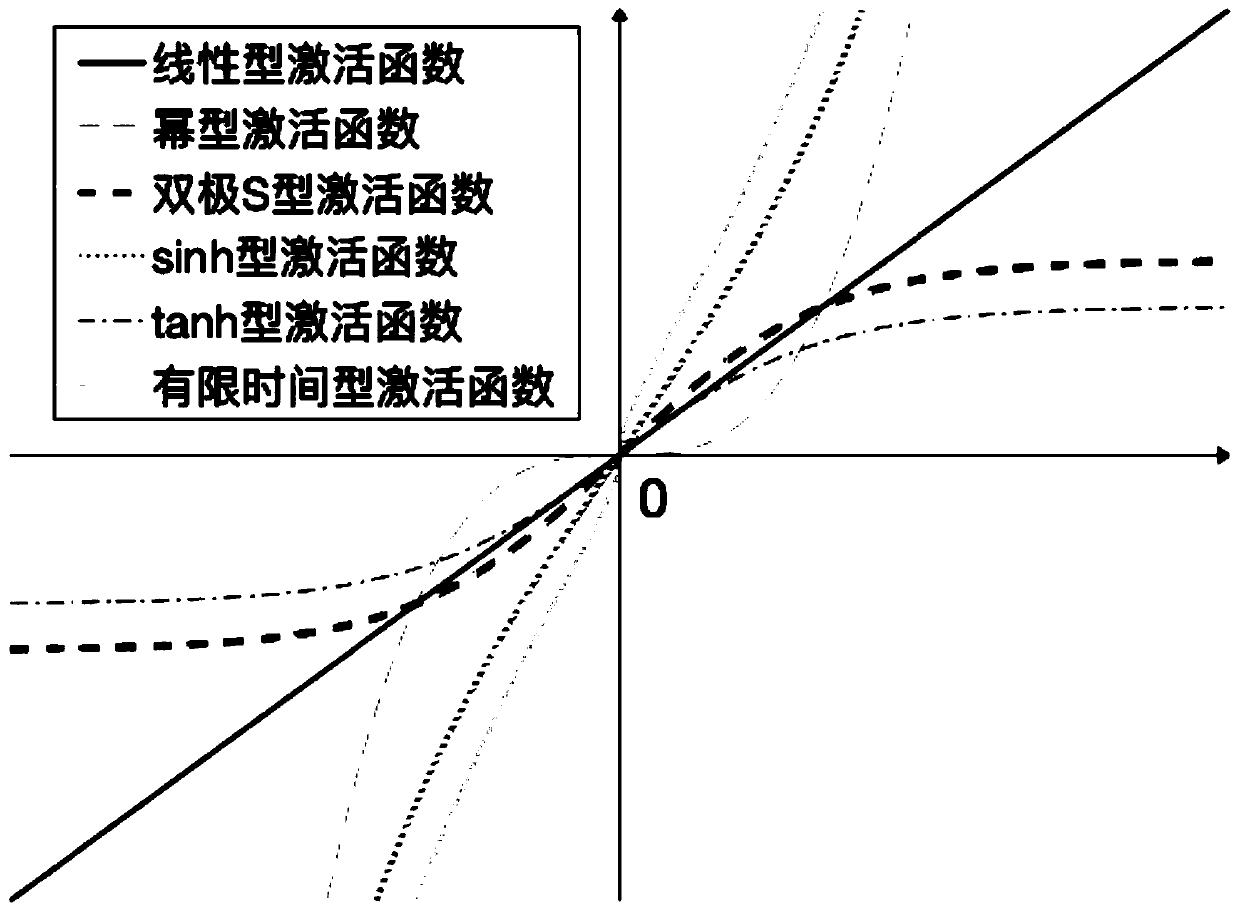
Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • A time-varying convex quadratic programming solver design method
  • A time-varying convex quadratic programming solver design method
  • A time-varying convex quadratic programming solver design method

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

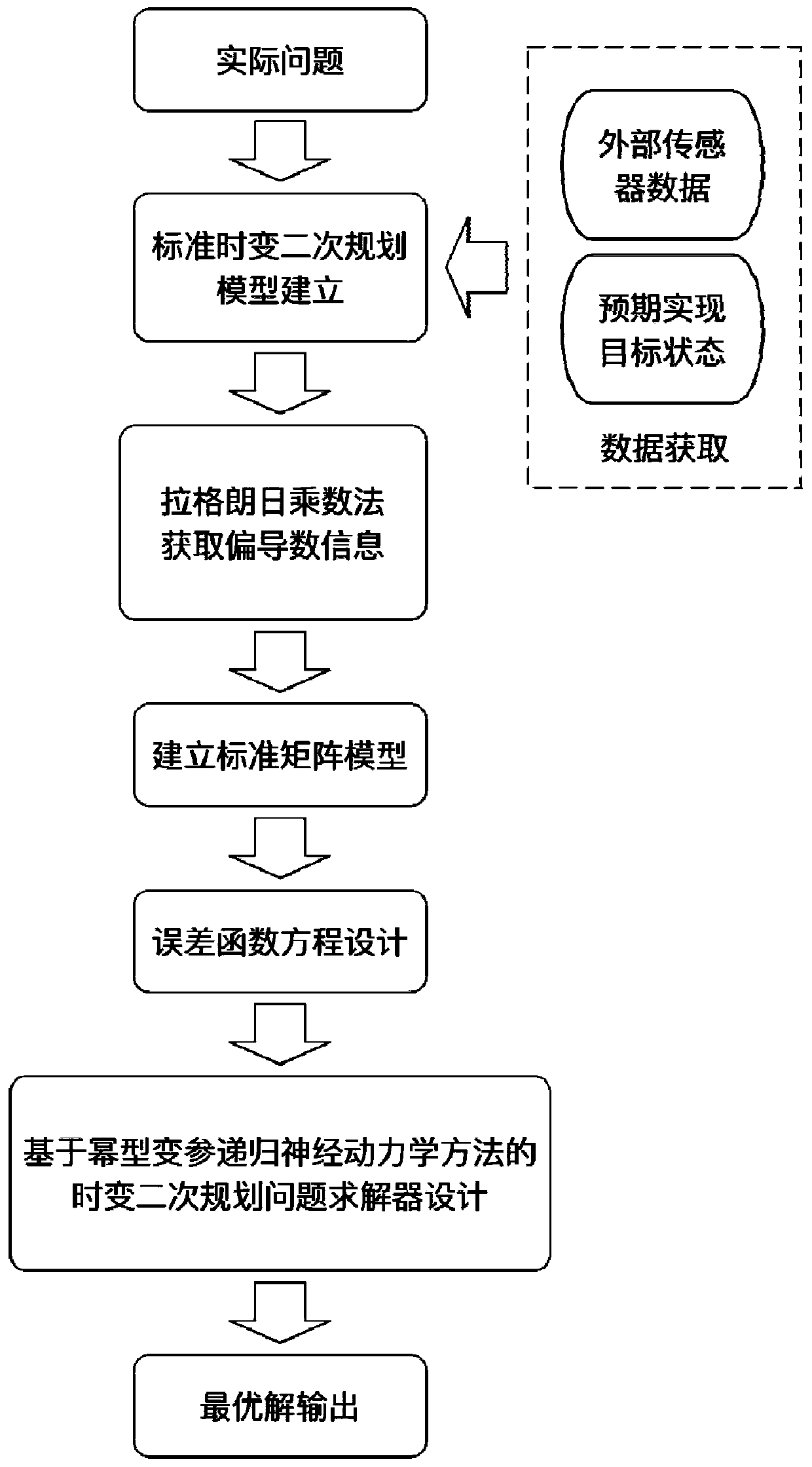
[0075] Such as figure 1 Shown is a flow chart of a time-varying convex quadratic programming solver design method of an example of the present invention; a design of a time-varying convex quadratic programming solver design method comprises the steps:

[0076] 1) Standardize the actual physical system or numerical solution in the form of a time-varying quadratic programming problem through mathematical modeling methods, and establish a standard quadratic programming problem model for the system;

[0077] 2) According to the Lagrangian multiplier method, respectively obtain the partial derivative information about the optimal solution and the Lagrange multiplier of the standard time-varying quadratic programming problem in step 1), and write the Lagrangian optimization formula;

[0078] 3) Transform the partial derivative information about the optimal solution and the Lagrange multiplier in step 2) into a standard time-varying matrix form, and write the time-varying matrix equa...

Embodiment 2

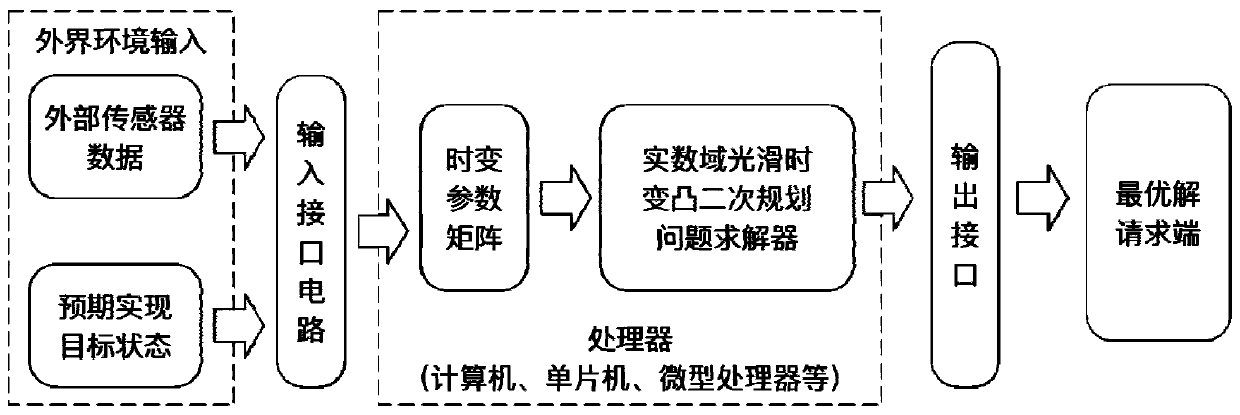
[0136] In order to demonstrate the actual system design process, an example is used to illustrate the problem: Assume that the time-varying parameter matrix of the system has been obtained, and consider a time-varying quadratic programming problem model in the real number domain with the following time-varying matrix

[0137]

[0138] subject to A(t)x(t)=B(t) (12)

[0139] in

[0140]

[0141] A(t):=[sin 2t cos2t], B(t):=cos3t, x(t):=[x 1 (t)x 2 (t)] T

[0142] According to formula (6), the above quadratic programming problem models (11)-(12) can be written in the following matrix equation form

[0143] W(t)Y(t)=G(t) (13)

[0144] in

[0145]

[0146] Y(t):=[x 1 (t) x 2 (t) λ(t)] T , G(t):=[-sin t -cos tcos 3t] T

[0147] According to the following implicit kinetic equation expression

[0148]

[0149] and to Definition

[0150] Y(t):=[x T (t),λ T (t)] T =[x 1 (t), x 2 (t),...,x n (t),λ 1 (t),λ 2 (t),...,λ m (t)] T (15)

[0151]The system ...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a time-varying convex quadratic programming solver design method. The method includes steps: establishing a time-varying quadratic programming standard model of a practical physical system through mathematical modeling; according to the Lagrange multiplier method, subjecting the quadratic programming standard model to optimal value solving to acquire optimal solution and Lagrange's multiplier related partial derivative information; converting the partial derivative information into a standard time-varying matrix form; designing an error functional equation according tothe standard time-varying matrix; according to the error functional equation and a power type varying-parameter recurrent neural dynamic method, designing a time-varying quadratic programming problempower type solver in a real number field through a monotone increasing odd activation function, so that a network state obtained through the time-varying quadratic programming problem power type solver is the optimal solution to the practical physical system or numerical solution time-varying quadratic programming problems. The time-varying convex quadratic programming solver design method has global convergence characteristics, errors can be converged to zero at a super-exponential speed, and accordingly calculation speed is greatly increased.

Description

technical field [0001] The patent of the invention belongs to the design method of the solver of the time-varying quadratic programming problem in the real number domain, and in particular relates to a recursive neural dynamics method based on power-type variable parameters. Background technique [0002] Artificial Neural Network (ANN) is a research hotspot in the field of artificial intelligence since the 1980s. It abstracts the human brain neuron network from the perspective of information processing, establishes a simple model, and forms different networks according to different connection methods. In engineering and academia, it is often referred to directly as a neural network or a neural network. A neural network is an operational model consisting of a large number of nodes (or neurons) connected to each other. Each node (Node) represents a specific output function, called the activation function (Activation Function). Each connection between two nodes represents a ...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Patents(China)
IPC IPC(8): G06F30/27
CPCG06F30/20
Inventor 张智军孔令东
Owner SOUTH CHINA UNIV OF TECH
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com