Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

H8 fault tolerance control method for networked linear parameter variation system with time variation and time delay

A linear parameter change, fault-tolerant control technology, applied in the direction of adaptive control, general control system, control/regulation system, etc., can solve problems such as property loss, even casualties, and difficult repairs

Active Publication Date: 2018-08-21
龙岩荣创信息科技有限公司
View PDF10 Cites 12 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

Many practical systems can be described by such models, such as aircraft systems, wind energy conversion systems, etc. Once such complex systems fail, it may cause major property losses and even casualties. Therefore, it is necessary to study how to reduce catastrophic accidents It is of great social and economic significance to improve the reliability and safety of modern complex control systems.
Especially due to the application of the network, there may be a certain distance between the controller and the actuator, once a failure occurs, it is difficult to repair it in time

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • H8 fault tolerance control method for networked linear parameter variation system with time variation and time delay
  • H8 fault tolerance control method for networked linear parameter variation system with time variation and time delay
  • H8 fault tolerance control method for networked linear parameter variation system with time variation and time delay

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

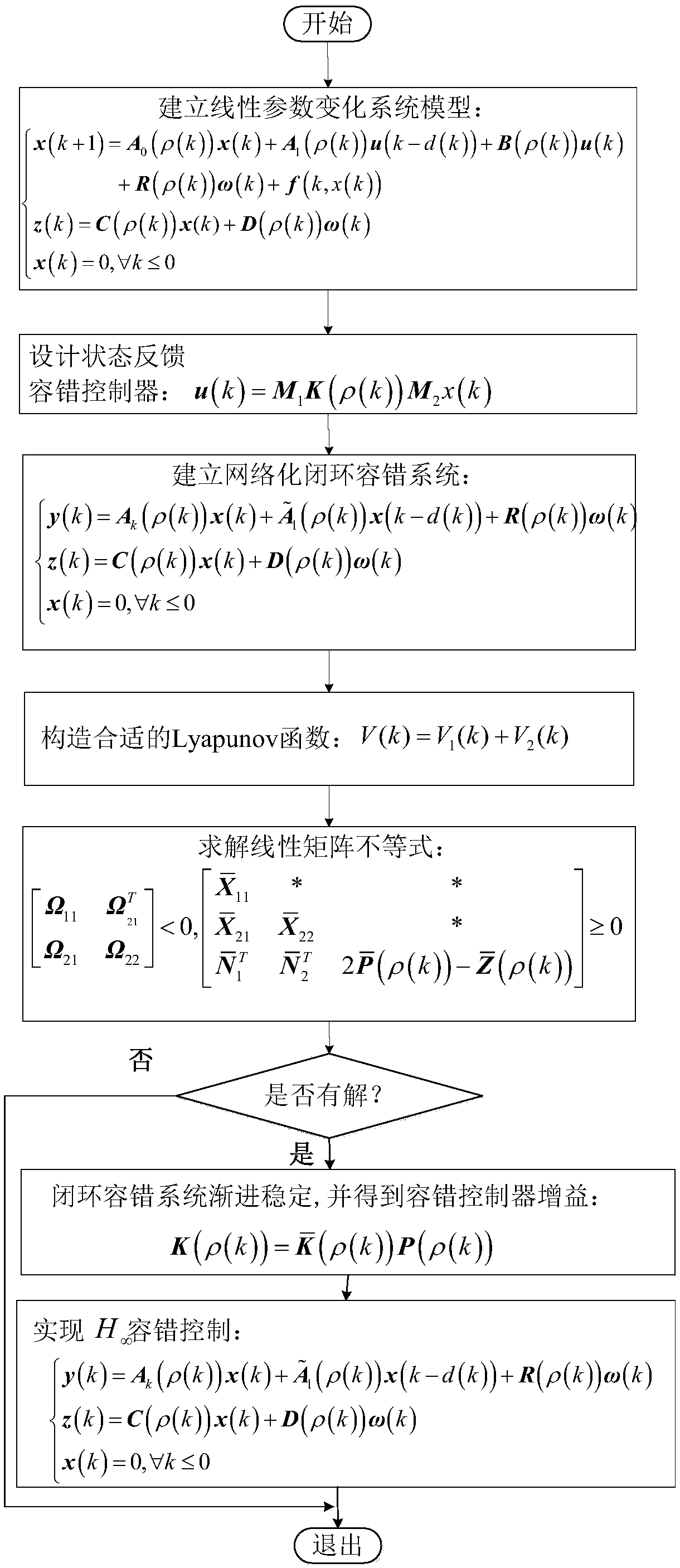
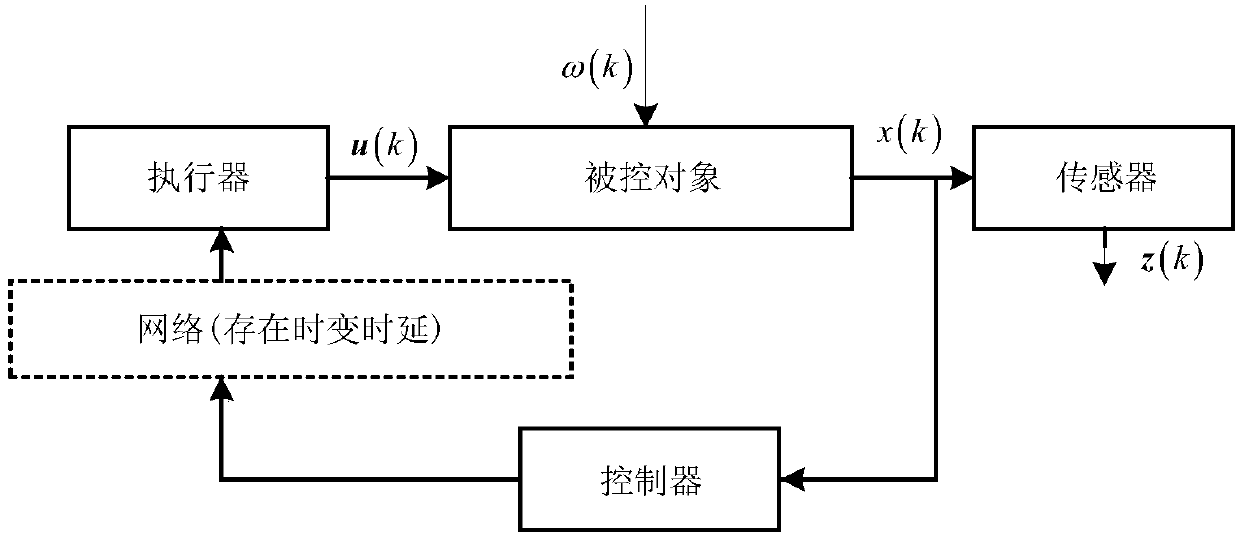
[0054] as attached figure 1 As shown, the H of a class of networked linear parameter changing system with time-varying delay ∞ A fault-tolerant control method, comprising the following steps:

[0055] Step 1: Establish a linear parameter changing system model with time-varying delay as formula (1).

[0056] Step 2: Design the state feedback controller as formula (2), and establish the closed-loop fault-tolerant control system of networked linear parameter change system with time-varying time delay as formula (3).

[0057] Step 3: Construct the Lyapunov function as formula (4).

[0058] Step 4: Based on the Lyapunov function constructed in step 4, using the Lyapunov stability theory and linear matrix inequality analysis method, the closed-loop fault-tolerant control system with time-varying delay and networked linear parameter variation system is asymptotically stable and H ∞ The sufficient condition for the existence of the controller is that matrix inequalities (5) and (6)...

Embodiment 2

[0062] Adopt the H of a class of networked linear parameter change system with time-varying time delay that the present invention proposes ∞ The fault-tolerant control method, the specific implementation method is as follows:

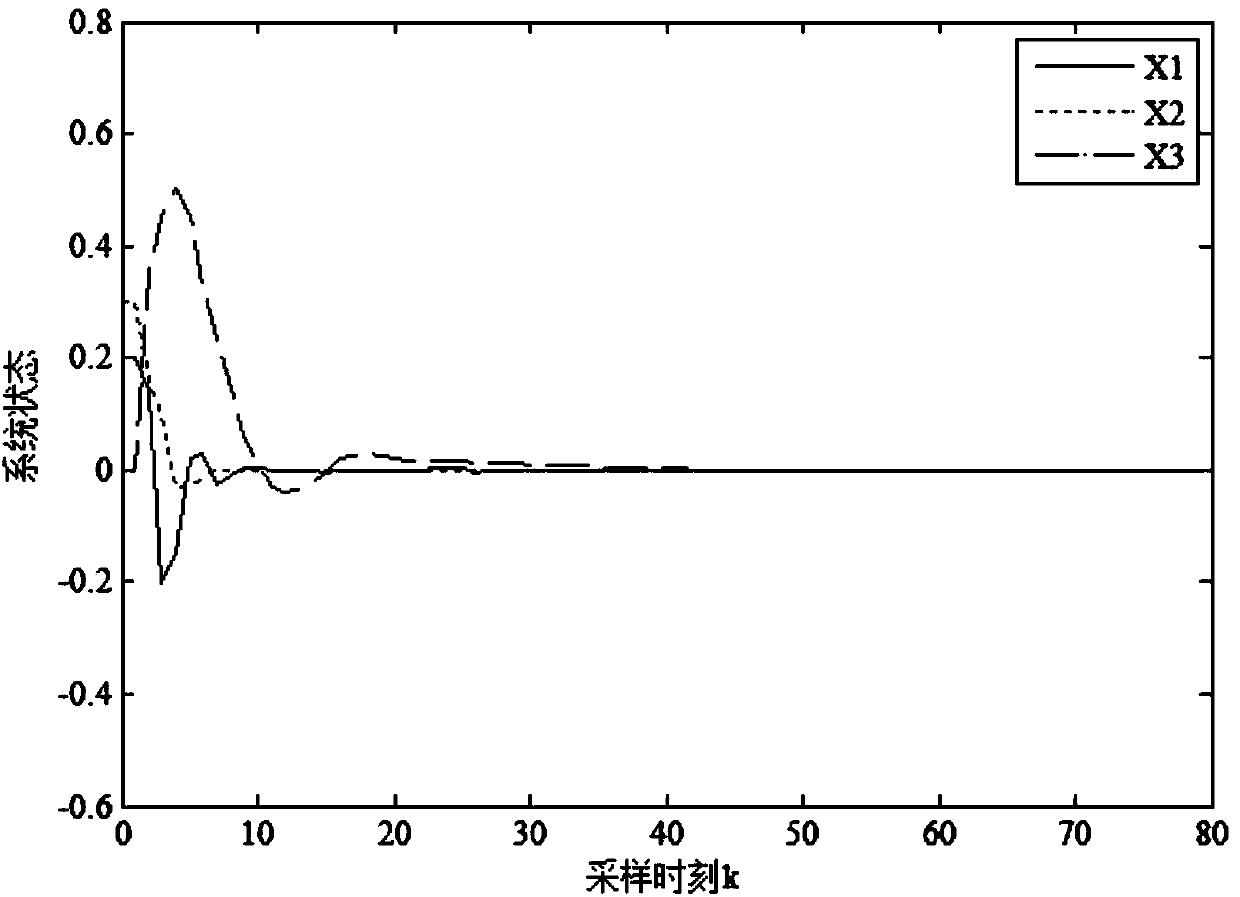
[0063] A wind energy generator is transformed into a linear parameter change system, its mathematical model is formula (1), and its system parameters are given as:

[0064]

[0065]

[0066]

[0067]

[0068] Among them, ρ(k)=sin(k) 2 is a time-varying parameter, and the disturbance signal is selected as ω(k)=e -0.1ksin(πk) .

[0069] Choose 3 random failure scenarios:

[0070] a) Actuator random failure M 1 expectations for The mean square error is α 2 =diag{0.3,0.2,0.1}, the expectation of random sensor failures The mean square error is β 2 =diag{0.2,0.2,0.1}, delay upper bound d 2 = 2;

[0071] b) The expected random failure of the actuator is The mean square error is α 2 =diag{0.3,0.2,0.1}, the expectation of random sensor...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention provides an H8 fault tolerance control method for a networked linear parameter variation system with time variation and time delay, and belongs to the field of networked linear parametervariation system control. The method takes the situations that a linear parameter variation system has network time variation and time delay and a sensor and an executor break down simultaneously inaccount, firstly a method of free-weighting matrix is used to establish a Lyapunov function for processing the time variation and time delay to obtain sufficient conditions of closed-loop fault tolerance control system stability, then a Lyapunov theorem of stability and a linear matrix inequality analysis method are used to obtain sufficient conditions of H8 fault tolerance controller existence, lastly an approximate primary function and a gridding technology are used to approximate a solving problem of an infinite dimensional linear matrix inequality system with a solving problem of a finitedimensional linear matrix inequality system, a Matlab LMI toolkit is used for solution, and a gain matrix of an H8 fault tolerance controller is provided. The H8 fault tolerance control method for thenetworked linear parameter variation system with the time variation and the time delay reduces the conservatism of the H8 fault tolerance controller.

Description

technical field [0001] The invention belongs to the control field of networked linear parameter change systems, and relates to a class of networked linear parameter change systems with time-varying delay. ∞ fault-tolerant control method. Background technique [0002] Linear Parameter-Varying (LPV) system is a kind of system whose parameters are constantly changing. The elements of the state matrix of this type of system are definite functions with time-varying parameters, and the range of time-varying parameters related to the function can be measured. Many practical systems can be described by such models, such as aircraft systems, wind energy conversion systems, etc. Once such complex systems fail, it may cause major property losses and even casualties. Therefore, it is necessary to study how to reduce catastrophic accidents It is of great social and economic significance to improve the reliability and safety of modern complex control systems. Especially due to the appl...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): G05B13/04
CPCG05B13/042
Inventor 潘丰陈冬杰邹金鹏程麒
Owner 龙岩荣创信息科技有限公司
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com