Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

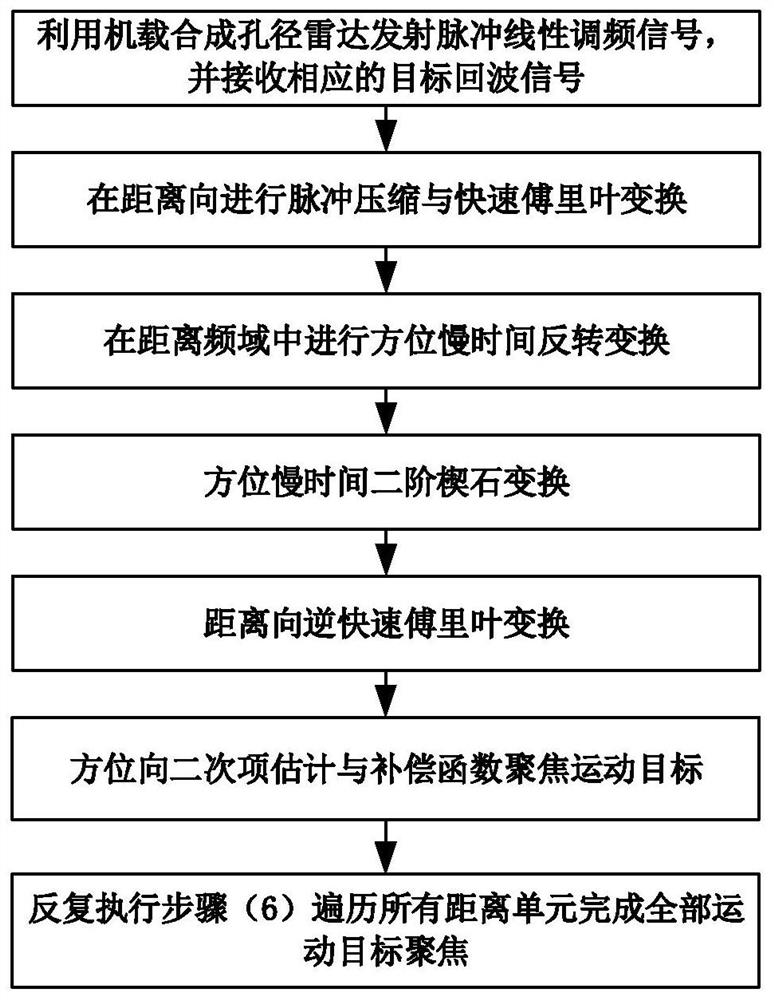
Focusing Method of Moving Target Based on Keystone Transformation and Integral Quadratic Function

A moving target and quadratic function technology, applied in the radar field, can solve problems affecting the focusing performance of the final moving target, and achieve the effects of improving focusing imaging performance, suppressing defocus, and improving performance

Active Publication Date: 2021-04-30
XIDIAN UNIV
View PDF5 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

Severely affects the performance of the final moving target focus

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Focusing Method of Moving Target Based on Keystone Transformation and Integral Quadratic Function
  • Focusing Method of Moving Target Based on Keystone Transformation and Integral Quadratic Function
  • Focusing Method of Moving Target Based on Keystone Transformation and Integral Quadratic Function

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

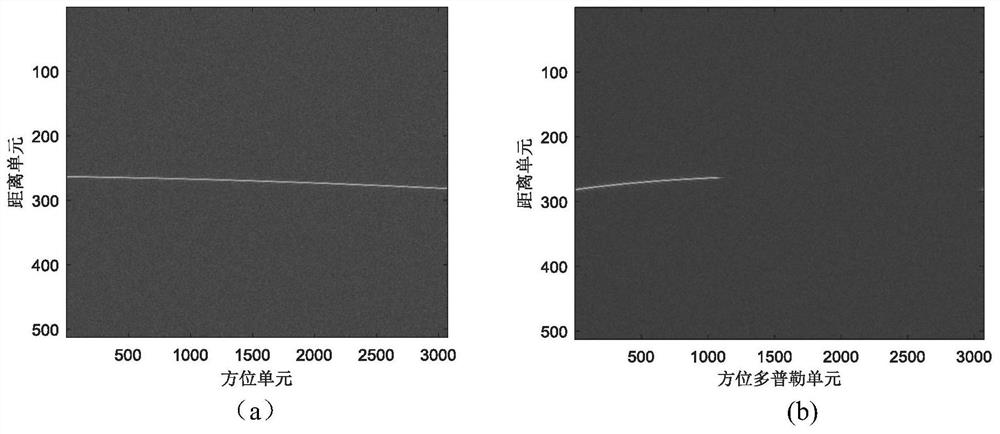
[0023] Ground moving targets inevitably exist in the radar detection scene. Radar is of great significance to the detection of ground moving targets. In this way, the moving targets in the ground hotspots can be observed, and the information of the moving targets can be obtained. Due to the movement characteristics of the moving target, the energy diffuses in the distance and Doppler dimension. In order to better observe the moving target, it is necessary to focus on the energy of the moving target. The existing focusing methods often do not consider the maneuvering of the moving target. characteristics, only consider the uniform motion, and only compensate for the low-order range migration and Doppler migration of the moving target, while ignoring the high-order range migration and Doppler migration of the moving target. At the same time, the use of search compensation for Doppler center ambiguity targets cannot better solve the energy defocus of moving targets caused by Dop...

Embodiment 2

[0033] The moving target focusing method based on keystone transformation and integral quadratic function is the same as embodiment 1, wherein in the step (3), the azimuth slow time reversal transformation is carried out in the distance frequency domain, specifically including the following steps:

[0034] 3a) Obtain the radar echo signal s in the range frequency domain and azimuth slow time domain for step 2 1 (f,t m ) to perform azimuth slow time reversal to obtain the radar echo signal after range frequency domain and azimuth slow time reversal Its specific calculation expression is:

[0035]

[0036] in: Represents the time series inversion operation, f represents the distance frequency variable, t m Indicates the azimuth slow time variable, m indicates the azimuth pulse number, rect(·) indicates the rectangular window function, B indicates the transmitted signal bandwidth, w a (t m ) represents the azimuth slow time window function, c represents the speed of lig...

Embodiment 3

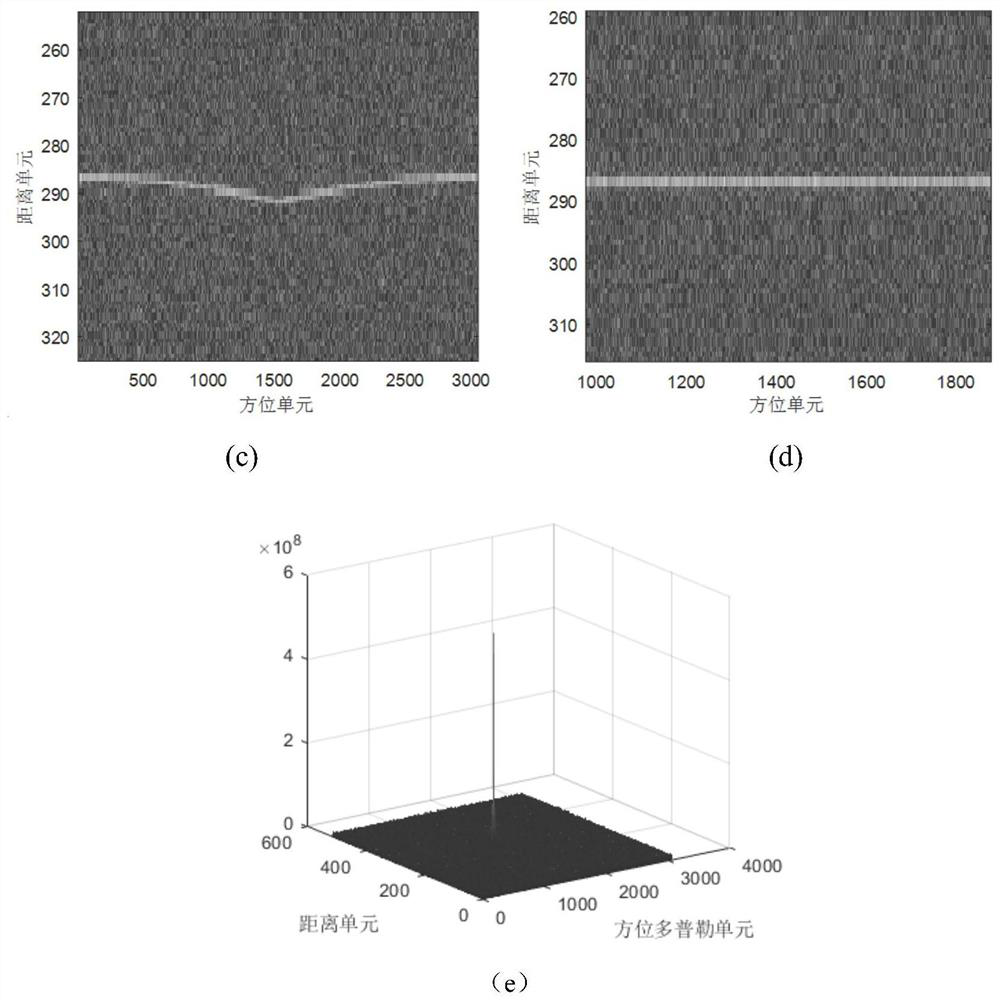
[0041] The moving target focusing method based on keystone transformation and integral quadratic function is the same as embodiment 1-2, wherein step (6) estimation and compensation of quadratic term in azimuth direction specifically includes the following steps:

[0042] 6a) Extract the echo signal of the moving target: extract the echo signal s of the moving target in the nth distance unit in the fast time of range and slow time of azimuth 2KT (R 0n , η m ):

[0043]

[0044] where: R 0n Indicates the nth distance unit, η m Indicates the azimuth slow time variable after keystone transformation, a 2n Represents the second-order item coefficient of the moving target distance model in the nth distance unit, n=1, 2,..., N represents the sequence number of the distance unit, and N represents the total number of distance units;

[0045] 6b) Calculate the integral quadratic function value: set the search range u=(-k,-k+Δk,...k-Δk,k) of the second-order coefficient of the ta...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention provides a moving target focusing method based on keystone transformation and integral quadratic function, which mainly solves the problem that the existing moving target focusing method cannot effectively compensate the high-order distance and Doppler migration of the moving target. The implementation steps are: transmit pulse chirp signal and receive radar echo; read radar echo signal to perform range-to-pulse compression and fast Fourier transform; perform azimuth slow-time inversion transformation in range-frequency domain; The signal after the slow time reversal transformation is subjected to second-order keystone transformation; the signal after the second-order keystone transformation is subjected to inverse fast Fourier transformation in the range frequency domain; the azimuth slow time signal of a single range unit is extracted and processed by an integral quadratic function , estimate the quadratic term, construct a compensation function to focus on moving targets, and traverse all distance units to focus on all targets. The invention can effectively compensate the high-order distance and Doppler migration of the moving target, and is used for focusing and imaging the moving target of the synthetic aperture radar.

Description

technical field [0001] The invention belongs to the technical field of radar, and in particular relates to focused imaging of a moving target, in particular to a moving target focusing method based on keystone transformation and integral quadratic function, which can be used for focused imaging of a synthetic aperture radar moving target. Background technique [0002] Synthetic Aperture Radar (SAR) is a high-resolution imaging system. Because of its all-day, all-weather, and low environmental dependence, it is widely used in military / civilian fields. However, there are unavoidable ground moving targets in the radar detection scene. Radar is of great significance to the detection of ground moving targets, such as the assessment of the battlefield situation and the monitoring of traffic conditions. Combining SAR technology with Ground Moving Target Indication (GMTI) technology can not only observe fixed targets in ground hot spots, but also obtain information about moving ta...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Patents(China)
IPC IPC(8): G01S13/90
CPCG01S13/904G01S13/9047G01S13/9011G01S13/9029
Inventor 周宇万俊张林让陈展野
Owner XIDIAN UNIV
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com