Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Target tracking method under arbitrary linear constraints

A target tracking and straight line technology, applied in the field of target tracking, can solve problems such as modeling and state estimation methods without arbitrary straight line constraints

Active Publication Date: 2018-11-13
HARBIN INST OF TECH
View PDF3 Cites 13 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0006] The technical problem to be solved by the present invention is to solve the problem that the prior art does not aim at any linear constraint modeling and state estimation method

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Target tracking method under arbitrary linear constraints
  • Target tracking method under arbitrary linear constraints
  • Target tracking method under arbitrary linear constraints

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

[0093] A method for tracking a target under arbitrary straight line constraints provided by an embodiment of the present invention includes the following steps:

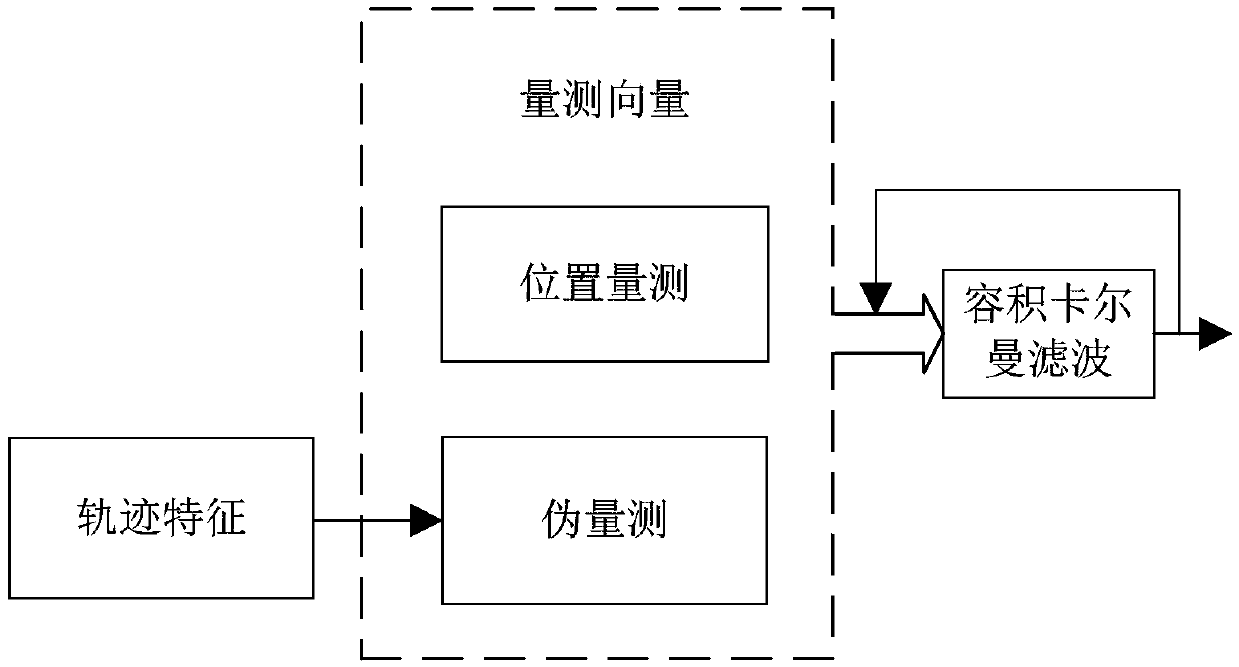
[0094] S1. Obtain the target position measurement information from the observation radar to construct a measurement vector, which includes the distance measurement of the target relative to the origin of the observation radar coordinate system and azimuth measurement

[0095] Obtaining target position measurement information from the observation radar during the tracking process is an existing technology, how the observation radar obtains this information, and how the method of the embodiment of the present invention obtains this information from the radar, those skilled in the art can adopt the existing technology It can be realized in various ways, and no matter which method is adopted, it is within the protection scope of the present invention.

[0096] S2. Use the state vector x of the target in the past k A...

Embodiment 2

[0102] Embodiment 2 is basically the same as Embodiment 1, and the similarities will not be described in detail. The difference lies in:

[0103] In step S2 of this embodiment, the target motion model under the Cartesian coordinate system is established, and the state equation of the target motion model is:

[0104] x k+1 = Φ k x k +Γ k v k

[0105] where x k is the state vector at time k, and the subscript is the corresponding time, including the position component x along the x and y directions at time k k 、y k , and the velocity component x k+1 is the state vector at time k+1; Φ k is the state transition matrix; v k is the process noise vector, assuming that the process noise is Gaussian white noise with known zero mean variance, and its process noise covariance matrix is ​​cov(v k )=Q k ≥0; k is the noise distribution matrix.

[0106] Preferably, in the step S1, the near-constant velocity model (NCV) is used as the target motion model in the linear moving t...

Embodiment 3

[0118] The third embodiment is basically the same as the second embodiment, and the similarities will not be repeated. The difference lies in:

[0119] In step S3 of this embodiment, the augmented state is used to construct a pseudo-measurement to describe any linear constraint relationship, and the pseudo-measurement in the Cartesian coordinate system is obtained as:

[0120]

[0121] It can be seen that only the state components of the target position and velocity at time k and k-1 can be used to give a complete description of the constraint relationship. In fact, as long as d≥1, the description of the constraint relationship can be obtained through the above formula.

[0122] Preferably, the pseudo-measurement is augmented into the measurement vector, and the augmented measurement equation is obtained as:

[0123]

[0124] The corresponding measurement noise covariance matrix is:

[0125]

[0126] in, is the measurement vector at time k, is a function that ch...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention relates to a target tracking method under arbitrary linear constraints, comprising: acquiring target position measurement information from an observation radar to construct a measurementvector, wherein the measurement vector comprises distance measurement and azimuth measurement of a target relative to the original of an observation radar coordinate system; performing state augmentation of the state vector of the target at the current time point using the state vector of the target at previous time points to obtain an augmented state vector and its corresponding state equation,wherein the augmented state includes states of the k time point and the previous d consecutive time points, and d represents the time span of the augmented part; constructing pseudo-measurement according to the linear trajectory shape of the target motion to describe the arbitrary linear constraint relationship, and augmenting the pseudo-measurement into the measurement vector to obtain an augmented measurement equation; and using a nonlinear filtering method, and performing filtering by using the augmented state equation and the augmented measurement equation. The method constructs the pseudo-measurement, uses the linear trajectory shape information to improve the filtering precision, and provides a new solution for the target tracking problem under any linear constraints.

Description

technical field [0001] The invention relates to the technical field of target tracking, in particular to a target tracking method under arbitrary straight line constraints. Background technique [0002] Target tracking is when the system processes the measurements (distance, angle, Doppler velocity, etc.) from the target in order to maintain an estimate of the target's current state (position, velocity, acceleration, etc.). Constrained state estimation is a method for estimating the state of the target state under the condition of equality or inequality constraints. In many actual target tracking scenarios, the trajectory of the target is not completely determined by the speed of the target itself, but is affected or restricted by its physical environment or its own motion characteristics, which is not an unconstrained free movement. Reasonable use of the constraint information contained in these actual scenes can effectively improve the performance of state estimation and ...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): G01S13/72G01S13/00
CPCG01S13/006G01S13/72
Inventor 周共健李可毅
Owner HARBIN INST OF TECH
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com