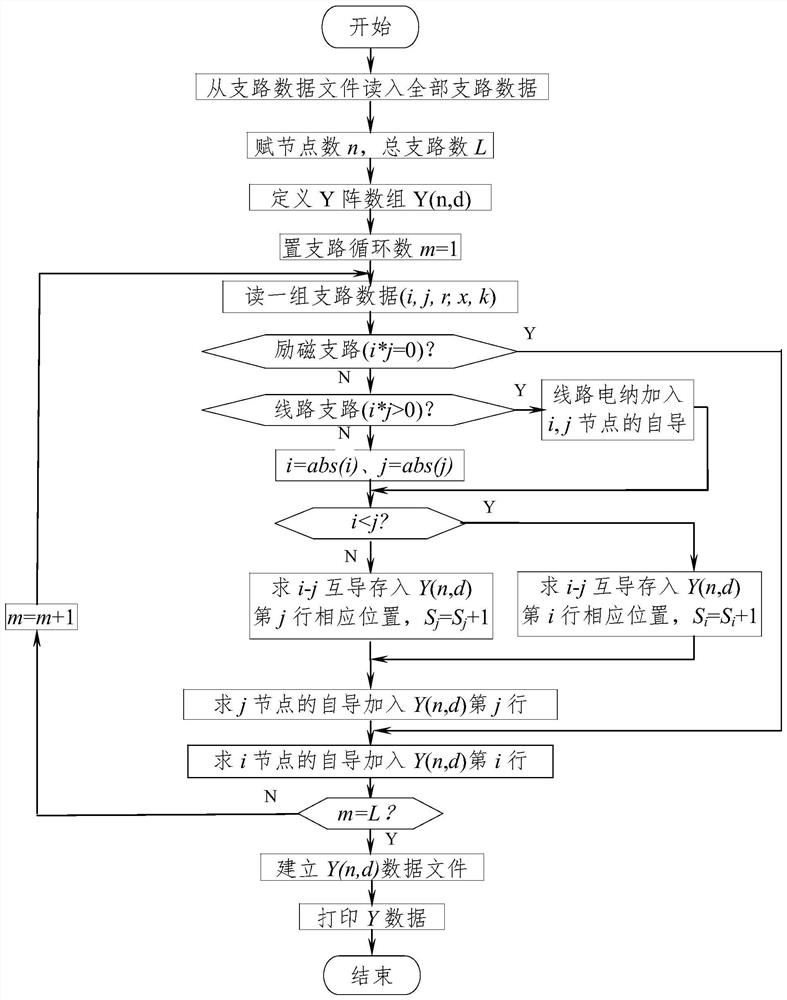
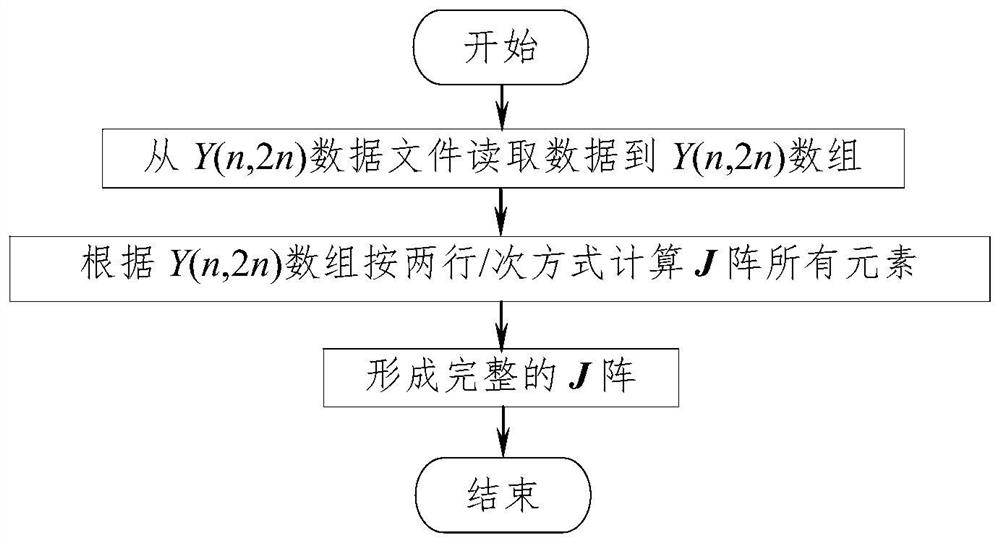
A method for fast formation of Jacobian matrix in power system power flow calculation

Abstract

A method for quickly forming a Jacobian matrix in power system power flow calculations, comprising: establishing an array Y(n,d) that only stores triangular non-zero elements on the Y array in a random order, and controls the number of non-zero elements with the number of non-zero elements Read and apply; accumulatively calculate the self-admittance of nodes i and j; calculate the mutual admittance of nodes i and j respectively, and calculate S cumulatively according to the number of mutual admittances i ;Write the Y(n,d) array into the data file; read the Y(n,d) data file and randomly calculate the node active current I according to the parameters of the Y(n,d) array pi and reactive current I qi ;According to Y array element and J ij and J ji The corresponding relation of sub-array non-zero element position, use Y(n,d) array element, calculate J array element according to two rows + two columns at the same time; According to I pi , I qi , modify all diagonal elements to form a complete J matrix. The calculation speeds of forming and storing Y-array data files, reading Y-array data files, and forming J-array are greatly superior to those of traditional methods, and the advantages become more obvious with the increase of system scale.

Description

technical field [0001] The invention belongs to the field of power system analysis and calculation, and relates to a method for randomly storing triangular non-zero elements on an admittance matrix and quickly forming a Jacobian matrix in power system power flow calculation. Background technique [0002] The extremely sparse node admittance matrix Y and Jacobian matrix J are widely used in power system calculations, where the Y matrix is ​​symmetric and the J matrix is ​​asymmetric. But if the element structure of array J is represented by J ij Sub-array representation, except for the balance node, the structure of Y array elements is the same as J in J array ij The structure of the subarrays is exactly the same. At this time, it can also be found that although the J array is asymmetrical, in the J array, the J ij Subarray with J ji The non-zero position of the sub-array is almost symmetrical, and this feature makes the elements of the Y array and J in the J array ij Su...

AI Technical Summary

Problems solved by technology

This form is simple and intuitive, and it is convenient to process the Y array data. However, due to the storage of a large number of zero elements, more storage units are required, and it takes a long time to read and write Y(n, 2n) data files.

Although the element structure in the Y(n,2n) array is similar to the element structure in the J array, the J array can be easily formed by using the Y(n,2n) array, but because the elements of the Y array and the J array are not used ij Subarray and J ji The relationship between the elements of the sub-array makes the formation of the J-array inefficient

[0004] In traditional methods, the coordinate method, sequential method, and linked list method, which consider the sparseness of Y array elements, have greatly reduced the storage units, but the diagonal elements are stored separately from the non-zero non-diagonal elements, which not only complicates the storage structure, but also is not conducive to data storage. retrieval, modification, and application, and its storage method has no clear corresponding relationship with the element structure of the Y array and J array, and it cannot reflect the relationship between the elements of the Y array and the J array. ij Subarray and J ji The relationship between the elements of the sub-arrays does not take advantage of the symmetry of the elements of the Y-array, which leads to the unsatisfactory speed of forming the Y-array or J-array

[0005] The Y(n ,22) The storage method, although the storage method of the triangular non-zero elements on the Y array is given, and the symmetry of the Y array elements is also used, but the specific calculation process is not given; in the process of forming the Y array, j 1 2 3 4 5 6 requirements, a large number of loops and judgment statements are required, which also leads to low calculation efficiency; this method is inconvenient to obtain the non-zero elements of the lower triangle, so the calculation of node active and reactive current I pi and I qi , node active and reactive power P i and Q i , Diagonal element H in array J ii , N ii , M ii , L ii It also causes inconvenient calculation; this method also does not use the structure of Y array elements and J ij and J ji The relationship corresponding to the position of the non-zero elements of the sub-array forms a J-array

Images