Check patentability & draft patents in minutes with Patsnap Eureka AI!

A method for obtain continuous gradient porous structure with minimal curved surface

A technology of extremely small surface and acquisition method, applied in the field of porous structure, can solve the problem of single performance, achieve the effect of large design freedom, simple calculation process, and wide application range

Active Publication Date: 2019-02-22
HUAZHONG UNIV OF SCI & TECH
View PDF3 Cites 14 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0005] Aiming at the above defects or improvement needs of the prior art, the present invention provides a method for obtaining a continuous gradient porous structure with a minimal curved surface. By establishing a three-dimensional space region and defining feature points in the region, according to the required gradient porous structure According to the requirements of porosity, the eigenvalues ​​of each feature point are assigned to obtain the minimum surface model, and finally the continuous gradient minimum surface porous structure is generated according to the minimum surface model, which overcomes the shortcomings of the traditional uniform porous porous structure. Fabrication of gradient porous materials suitable for complex mechanical environments

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • A method for obtain continuous gradient porous structure with minimal curved surface

Examples

Experimental program
Comparison scheme
Effect test

example 1

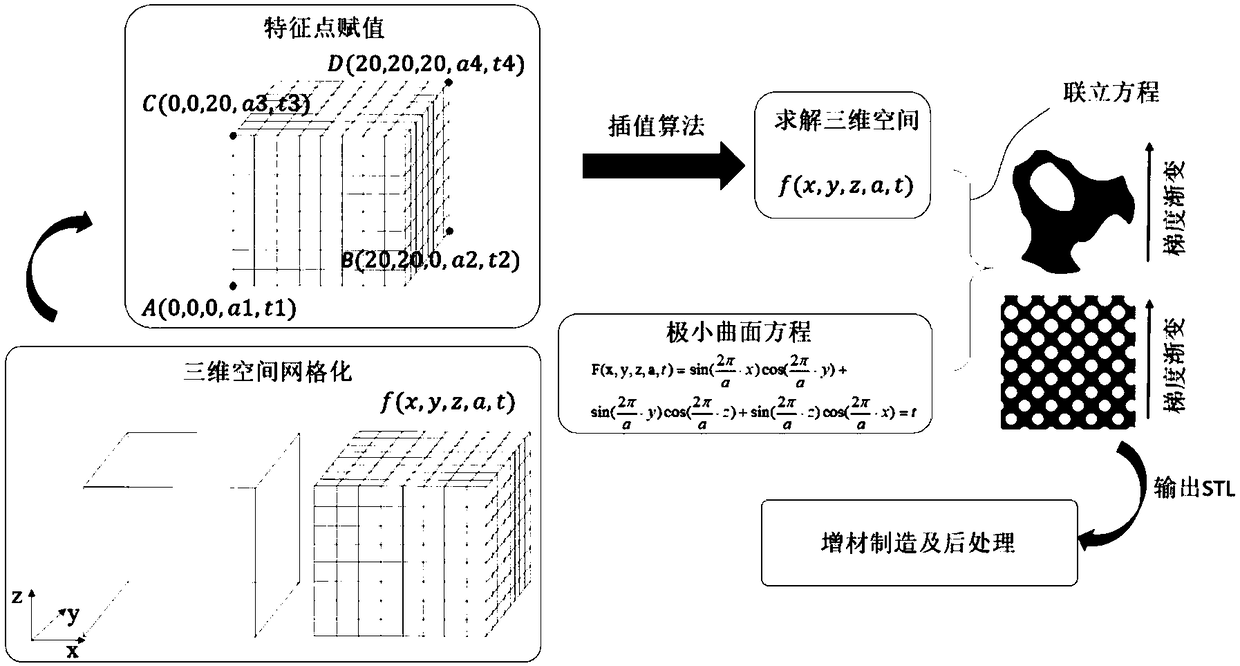
[0034] (1) Establish a spatial range R, where 0≤x≤20, 0≤y≤20, 0≤z≤20, and divide the space into grids, and divide the space with a unit size of 0.05, then each direction of R There are 400 elements, 401 nodes. Establish a spatial function f(x, y, z, a, t), and assign the initial value 0 to a and t of each node.

[0035] (2) Define the characteristic points of the porous structure at different positions in the three-dimensional space: A(0,0,0,2.8,0.05), B(20,20,0,2.8,0.05), C(0,0,20 ,2.25,0.2), D(20,20,20,2.25,0.2).

[0036] (3) According to the feature points defined in step (2), use the interpolation algorithm to obtain the function f value of each point in the middle, such as AC1(0,0,5,2.663,0.0875), AC2(0,0,10, 2.525,0.125), AC3(0,0,15,2.3875,0.1625).

[0037] (4) Carry out the mathematical modeling of Schoen Gyroid porous structure according to f(x, y, z, a, t) at each point in space, b=5 in the formula (1), the value of t at each point can be used in the formula

[00...

example 2

[0042] (1) Establish a spatial range R, where 0≤x≤20, 0≤y≤20, 0≤z≤20, and divide the space into grids, and divide the space with a unit size of 0.05, then each direction of R There are 400 elements, 401 nodes. Establish a spatial function f(x, y, z, a, t), and assign the initial value 0 to a and t of each node.

[0043](2) Define the characteristic points of the porous structure at different positions in the three-dimensional space: A(0,0,0,2.65,0.075), B(20,20,0,2.65,0.075), C(0,0,20 ,2.25,0.2), D(20,20,20,2.25,0.2).

[0044] (3) According to the feature points defined in step (2), use the interpolation algorithm to obtain the function f value of each point in the middle, such as AC1(0,0,5,2.55,0.10625), AC2(0,0,10, 2.45,0.1375), AC3(0,0,15,2.35,0.16875).

[0045] (4) Carry out the mathematical modeling of Schoen Gyroid porous structure according to f(x, y, z, a, t) at each point in space, b=5 in the formula (1), the value of t at each point can be used in the formula

[...

example 3

[0050] (1) Establish a spatial range R, where 0≤x≤20, 0≤y≤20, 0≤z≤20, and divide the space into grids, and divide the space with a unit size of 0.05, then each direction of R There are 400 elements, 401 nodes. Establish a spatial function f(x, y, z, a, t), and assign the initial value 0 to a and t of each node.

[0051] (2) Define the characteristic points of the porous structure at different positions in the three-dimensional space: A(0,0,0,2.55,0.1), B(20,20,0,2.55,0.1), C(0,0,20 ,2.25,0.2), D(20,20,20,2.25,0.2).

[0052] (3) According to the feature points defined in step (2), use the interpolation algorithm to obtain the function f value of each point in the middle, such as AC1(0,0,5,2.475,0.125), AC2(0,0,10, 2.4,0.15), AC3(0,0,15,2.325,0.175).

[0053] (4) Carry out the mathematical modeling of Schoen Gyroid porous structure according to f(x, y, z, a, t) at each point in space, b=5 in the formula (1), the value of t at each point can be used in the formula

[0054] f(...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention belongs to the porous structure field, and discloses a method for obtaining a minimal curved surface continuous gradient porous structure. The method comprises the following steps: (a) establishing an Euler three-dimensional space region and meshing the Euler three-dimensional space region to obtain the coordinates of each node on the mesh, selecting a plurality of nodes as feature points in the network node, and setting the eigenvalue of each feature point as (x, y, z, a, t); (b) assigning values of a and t in eigenvalue of each of that characteristic points according to a gradient requirement of the porosity of the require minimal curved surface porous structure; (c) obtaining a minimal surface model according to the eigenvalue fitting corresponding to each feature point, and generating a porous structure of the minimal surface in a three-dimensional space region according to the model of the minimal surface, thereby obtaining a required continuous gradient minimal surface porous structure. The invention overcomes the disadvantage of single performance of the traditional uniform pore porous structure, and produces a gradient porous material suitable for complex mechanical environment.

Description

technical field [0001] The invention belongs to the field of porous structures, and more specifically relates to a method for obtaining a continuous gradient porous structure with minimal curved surfaces. Background technique [0002] Porous materials are widely used in lightweight design in aerospace, medical, transportation and other industries due to their excellent comprehensive properties such as impact resistance, energy absorption, heat insulation, and sound absorption. However, with the improvement of product performance and the demand for integrated design, simple lightweight and energy absorption characteristics can no longer meet the needs of high-performance components. For example, the most studied uniform porous lattice material has single mechanical properties and is difficult to change. , unable to match the mechanical performance requirements of "conformal change", [0003] As the data input for 3D printing, computer-aided design has attracted extensive att...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): G06F17/50G06F17/11
CPCG06F17/11G06F30/20
Inventor 闫春泽杨磊李昭青史玉升陈鹏伍宏志刘主峰
Owner HUAZHONG UNIV OF SCI & TECH
Features
  • R&D
  • Intellectual Property
  • Life Sciences
  • Materials
  • Tech Scout
Why Patsnap Eureka
  • Unparalleled Data Quality
  • Higher Quality Content
  • 60% Fewer Hallucinations
Social media
Patsnap Eureka Blog
Learn More

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com