Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

A non-structural grid nearest wall distance solving method based on a balanced KD tree

An unstructured grid, the closest distance technology, applied in the field of computational fluid dynamics and applied mathematics, can solve the problems of poor query efficiency in the far field area, large error in the nearest wall distance, unbalanced ADT tree, etc., to achieve easy implementation Parallelization, reduction of calculation amount, good practical effect

Pending Publication Date: 2019-06-28
AERODYNAMICS NAT KEY LAB
View PDF0 Cites 7 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

The selection of the size of the "box" in this type of method is highly empirical. When the size is larger, the query efficiency of the far-field area will be deteriorated. When the size is smaller, the nearest wall point may not fall in the box, thus The error of the nearest wall distance of the solution is large
In addition, when the grid distribution of the object surface is uneven, it will cause the imbalance of the ADT tree and seriously affect the query efficiency

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • A non-structural grid nearest wall distance solving method based on a balanced KD tree
  • A non-structural grid nearest wall distance solving method based on a balanced KD tree
  • A non-structural grid nearest wall distance solving method based on a balanced KD tree

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

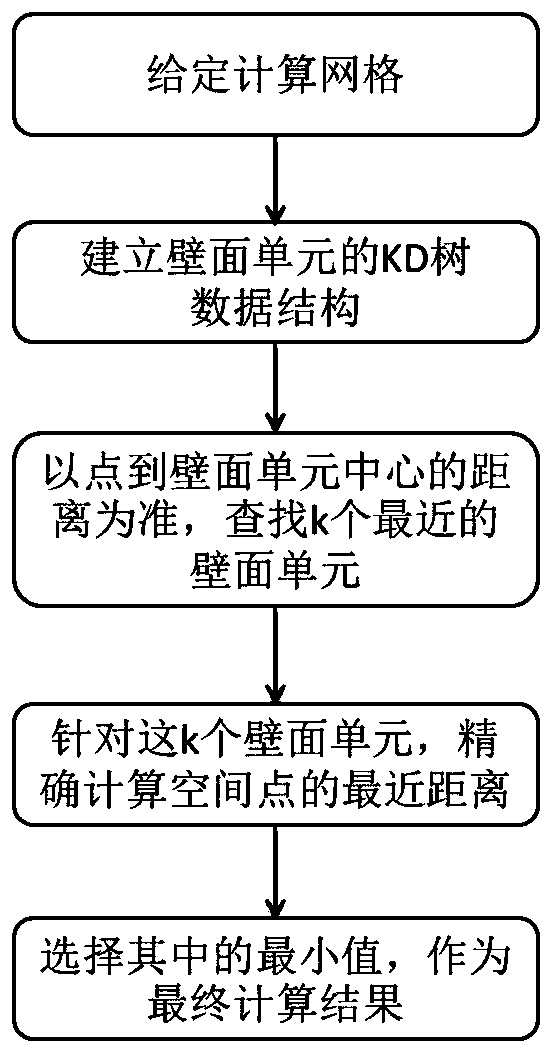
[0035] like figure 1 As shown, a method for solving the wall distance of an unstructured grid based on a balanced KD tree includes the following steps:

[0036] S1. Taking the coordinates of the center point of the wall unit as the dimension, establish a balanced KD tree data structure;

[0037] S2. For a certain target point in space, use the distance from it to the center point of the wall surface unit as the approximate shortest distance, start from the root node of the KD tree to query step by step, and select k nearest object surface units;

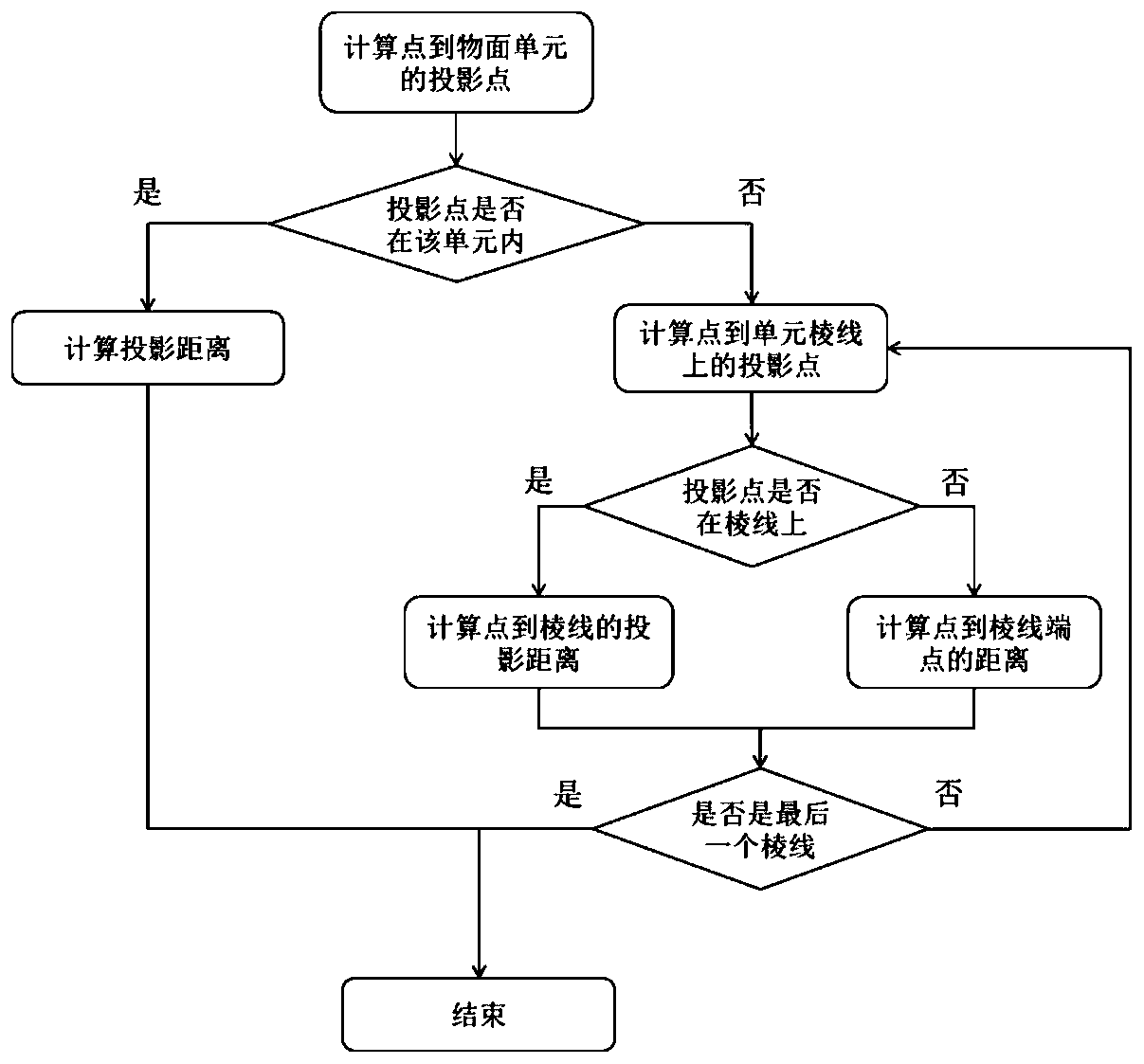
[0038] S3. After finding the k nearest object plane units based on the center point of the object plane unit, accurately calculate the shortest distance from the target point to the k object plane units, and select the minimum value among them as the final result.

Embodiment 2

[0040] This embodiment is on the basis of embodiment 1:

[0041] In step S1, taking the two-dimensional space point set {1, 2, ... N} as an example, the establishment process of the KD tree is as follows:

[0042] S11. First sort the x-coordinates of the points, and take the Floor(N / 2)th point as the root node;

[0043] S12. For the sorted subset (1~Floor(N / 2)-1), the y coordinates of the points are sorted, and the median point is taken as the left child node of the root node;

[0044] S13. For the sorted subset (Floor(N / 2)+1~N), sort the y coordinates of the points, and take the median point as the right child node of the root node;

[0045] S14. Recursively execute S11-S13, and make judgments starting from the x and y coordinates in turn until there is no point in the subset.

Embodiment 3

[0047] This embodiment is on the basis of embodiment 2:

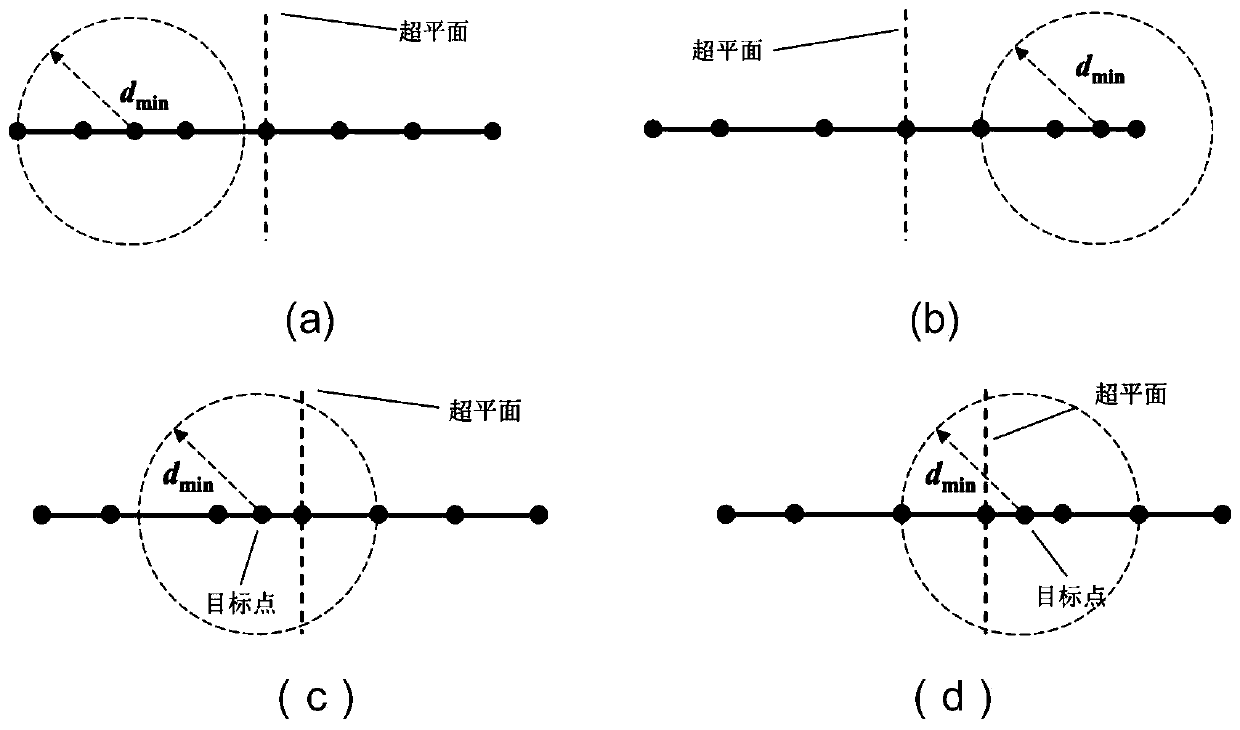
[0048] When selecting the query path, draw a circle (two-dimensional) or sphere (three-dimensional) with the target point as the center, using the currently calculated nearest wall distance as the radius, and draw a circle (or sphere), target point, hyperplane The relative position of determines the next child node to be queried. Taking the dimension x in the two-dimensional case as an example, the query method is as follows figure 2 As shown, the description is as follows:

[0049] a) If the target point is located on the left side of the current KD tree hyperplane, and its circumscribed circle does not intersect with the hyperplane, then directly enter the left subtree instead of entering the right subtree for query, wherein the circumscribed circle is the target point As the center, a sphere with the current minimum distance as the radius;

[0050] b) If the target point is located on the right side of the curren...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a non-structural grid nearest wall surface distance solving method based on a balanced KD tree. The method comprises the following steps: 1) establishing a balanced KD tree structure according to a central point of a wall surface unit; 2) for a certain target point in the space, searching k nearest wall surface units from the KD tree structure by taking the distance from the target point to the central point of the wall surface unit as an approximate nearest distance; and 3) aiming at the k wall surface units, accurately calculating the nearest distance between the target point and the k wall surface units, and selecting the minimum value as a calculation result. According to the method, the KD tree data structure of the object plane unit is established, and an optimized searching path and wall surface distance solving algorithm is adopted, so that the time complexity and the calculation amount of query are greatly reduced. According to the method, the calculation efficiency can be greatly improved on the premise of fully ensuring the calculation precision, and parallel calculation is easy to realize. Test results for thousands of thousands of magnitudes ofcalculation grids show that compared with a direct method, the method can shorten the calculation time by more than two orders of magnitudes.

Description

technical field [0001] The invention relates to the fields of computational fluid dynamics and applied mathematics, in particular to a method for solving the nearest wall distance of an unstructured grid based on a balanced KD tree. Background technique [0002] In CFD (Computational Fluid Dynamics, Computational Fluid Dynamics) numerical simulation, it is often necessary to solve the shortest distance from spatial grid points or grid cells to the wall. When the calculation grid scale is small, the direct search method of loop traversal can be used for calculation; for medium-scale calculation grids, satisfactory solution efficiency can also be obtained through parallel computing technology. However, with the further increase of the grid size, it will become very time-consuming to solve the wall distance by direct search method or simply using parallel computing technology, so it is necessary to explore a more efficient solution algorithm. [0003] In addition to the direct...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): G06F16/901G06F16/903
Inventor 常兴华张来平王年华马戎赵钟李明何磊何先耀邵帅
Owner AERODYNAMICS NAT KEY LAB
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com