Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Block Compressed Sensing Method Based on Adaptive Sampling and Smooth Projection

A block-based compressed sensing and adaptive sampling technology, applied in image analysis, image enhancement, instrumentation, etc., can solve the problems of high algorithm complexity and low reconstructed image quality, and achieve reduced algorithm complexity and fast reconstruction speed. , the effect of improving quality

Inactive Publication Date: 2020-12-18
QIQIHAR UNIVERSITY
View PDF8 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0009] The purpose of the present invention is to solve the problems of low quality of reconstructed images and high algorithm complexity in the prior art, and propose a block compression sensing method based on adaptive sampling and smooth projection

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Block Compressed Sensing Method Based on Adaptive Sampling and Smooth Projection
  • Block Compressed Sensing Method Based on Adaptive Sampling and Smooth Projection
  • Block Compressed Sensing Method Based on Adaptive Sampling and Smooth Projection

Examples

Experimental program
Comparison scheme
Effect test

specific Embodiment approach 1

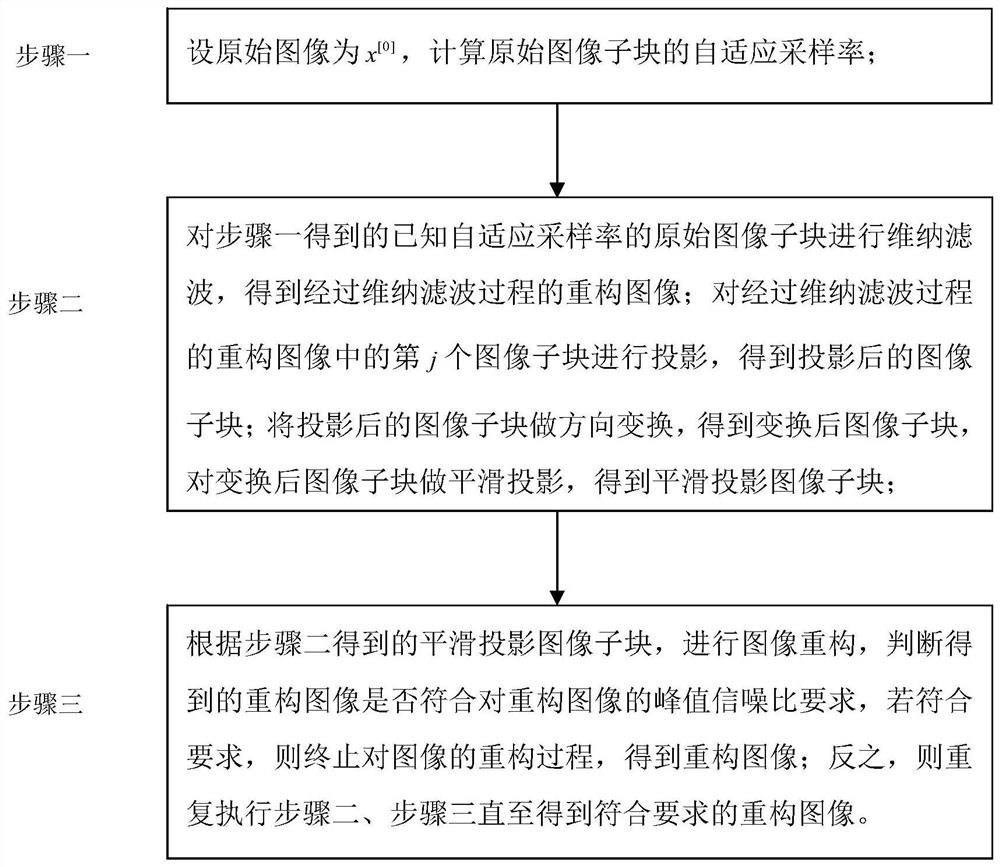
[0036] Specific implementation mode 1: The implementation mode of the present invention is based on the adaptive sampling and smooth projection block compression sensing method. The specific process is as follows:

[0037] Basic theory of compressed sensing

[0038] From the perspective of compressed sensing, to recover from M observations And M Φ is an M×N observation matrix, and its sampling rate is R=M / N. The CS theory points out that if x is sufficiently sparse under a certain transformation basis ψ, x can be recovered from y according to the following optimization method.

[0039]

[0040] As long as Φ and ψ are sufficiently uncorrelated, M is large enough. For high-dimensional signals such as image signals, when the sampling operator Φ is stored as a dense matrix, a large amount of storage space will be required. In addition, high dimensionality can make the reconstruction process time-consuming [13] . Therefore, for image sampling and reconstruction, more effic...

specific Embodiment approach 2

[0045] Specific embodiment 2: The difference between this embodiment and specific embodiment 1 is that in the step 1, the original image is set as x [0] , to calculate the adaptive sampling rate of the original image sub-block; the specific process is:

[0046] Calculation of Adaptive Sampling Rate

[0047] Using block-based compressed sensing algorithm (Block-based CS, BCS), the target image signal is first transformed into wavelet domain, and then divided into blocks of the same size but not overlapping. The size of each image block is B×B, using the same observation matrix Φ B Each image sub-block is observed separately. assuming x i is the original input image of the i-th block, then its output block can be expressed as

[0048] the y i = Φ B x i

[0049] In the formula, Φ B is the matrix for M B ×B 2 The observation matrix of Φ B Not associated with image blocks. x i is with B 2 A column vector of samples. In BCS, the entire measurement matrix Φ becomes a ...

specific Embodiment approach 3

[0061] Specific embodiment three: the difference between this embodiment and specific embodiment one or two is that the ith high-frequency sub-band (Y) is calculated in the step one or three (i) energy E i ; The specific process is:

[0062] i-th high-frequency sub-band (Y) (i) energy E i The expression is:

[0063]

[0064] In the formula, c(m,n) represents the i-th high-frequency subband (Y) (i) The coefficient at the (m,n) position in the middle; P and Q respectively represent the i-th high-frequency subband (Y) (i) Rows and columns; (m,n) represents the i-th high-frequency subband (Y) (i) location point.

[0065] Other steps and parameters are the same as those in Embodiment 1 or Embodiment 2.

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

A block compressed sensing method based on adaptive sampling and smooth projection. The present invention relates to a block compressed sensing method. The purpose of the invention is to solve the problems of low reconstructed image quality and high algorithm complexity in the prior art. The process is: 1. Assume the original image and calculate the adaptive sampling rate of the original image sub-block; 2. Perform Wiener filtering on the original image sub-block with known adaptive sampling rate to obtain the re-processed image after the Wiener filtering process. Compose the image; project the jth image sub-block in the reconstructed image to obtain the image sub-block; perform direction transformation to obtain the transformed image sub-block, perform smooth projection to obtain the smooth projected image sub-block; 3. According to the smooth projection Image sub-block, perform image reconstruction, and determine whether the reconstructed image meets the peak signal-to-noise ratio requirements of the reconstructed image. If it meets the requirements, the reconstructed image is obtained; otherwise, repeat steps 2 and 3 until the required peak signal-to-noise ratio is obtained. Reconstruct the image. The invention is used in the field of image reconstruction.

Description

technical field [0001] The invention relates to a block-compressed sensing method. Background technique [0002] The traditional sampling theorem requires that the sampling frequency be at least twice the signal bandwidth in order to fully restore the original signal. With the increase of signal bandwidth, the traditional sampling theorem requires higher and higher sampling rate. With the introduction of the concept of compressive sensing (CS), because it allows sampling and compression at the same time, and requires a very low sampling rate, compressed sensing quickly becomes a research hotspot. [1-2] ([1]Candes E J, Romberg J, Tao T.Robustuncertainty principles: exact signal reconstruction from highly incomplete frequency information[J].IEEE Transactions on Information Theory,2006,52(2):489-509.[2]Candes E J, Tao T. Near-Optimal Signal Recovery From Random Projections: Universal Encoding Strategies [J]. IEEE Transactions on Information Theory, 2006, 52(12): 5406-5425.). ...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Patents(China)
IPC IPC(8): G06T5/00G06T5/10
CPCG06T5/10G06T2207/20064G06T2207/10004G06T5/73G06T5/70
Inventor 石翠萍苗凤娟陶佰睿靳展黄柏锋王天毅
Owner QIQIHAR UNIVERSITY
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com