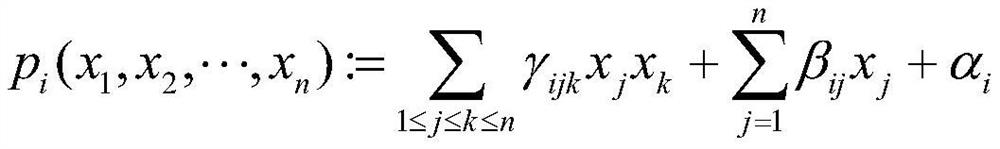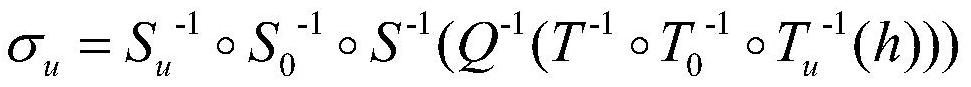Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Multi-variable broadcast multi-signature method based on certificateless

A multi-signature, multi-variable technology, applied in the field of network information security

Active Publication Date: 2022-03-04
XIAN UNIV OF POSTS & TELECOMM
View PDF2 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

However, there is currently no multi-variable broadcast multi-signature method based on certificates. How to construct multi-variable broadcast multi-signatures using certificateless public key cryptography is a technical problem that needs to be solved urgently in cryptography.

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Multi-variable broadcast multi-signature method based on certificateless
  • Multi-variable broadcast multi-signature method based on certificateless
  • Multi-variable broadcast multi-signature method based on certificateless

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

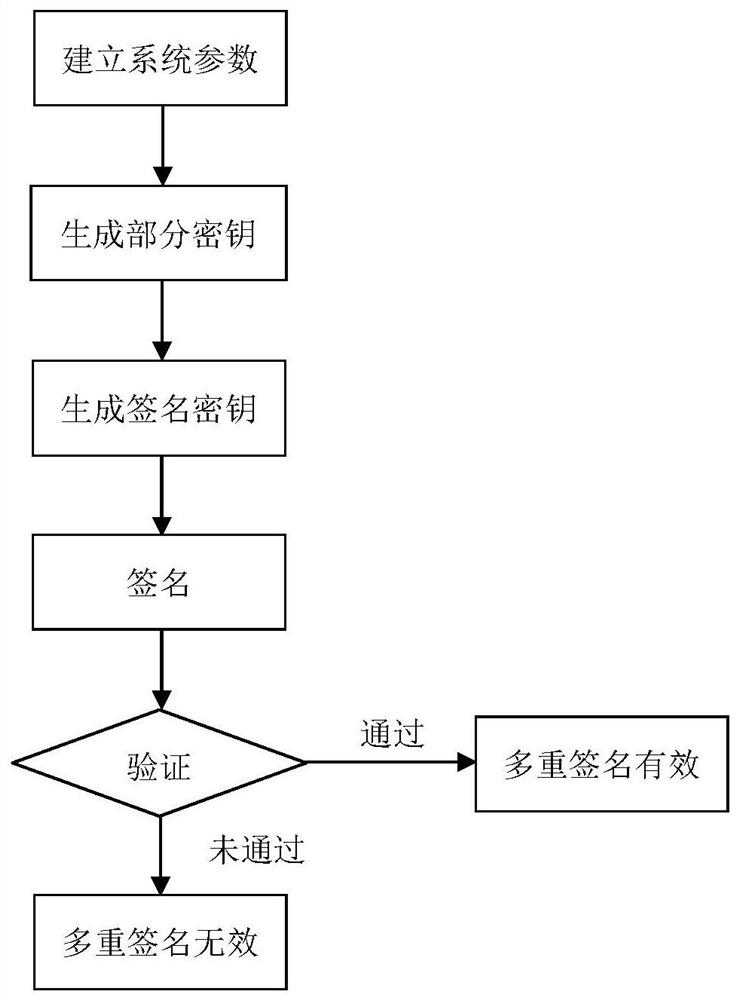
[0063] In this embodiment, the finite field K whose feature p is 2, order q is 256, n is 42, and r is 24 multivariate equations is taken as an example. The multivariate broadcast multi-signature method based on no certificate consists of the following steps (such as figure 1 shown):

[0064] A. Establish system parameters

[0065] (A1) The key generation center defines a finite field K with feature p and order q. In this embodiment, p is 2 and order q is 256.

[0066] (A2) The key generation center defines n-ary r multivariate equations on the finite field K. In this embodiment, n is 42 and r is 24.

[0067] P=(p 1 (x 1 ,x 2 ,···,x 42 ),···,p i (x 1 ,x 2 ,···,x 42 ),···,p 24 (x 1 ,x 2 ,···,x 42 ))

[0068] Each equation system p i is about the variable x being x 1 、x 2 ,...,x 42 The nonlinear quadratic equation for , where i is 1, 2, ..., 24:

[0069]

[0070] Among them, each coefficient α, β, γ and variable x are in the finite field K.

[0071] (A3) Th...

Embodiment 2

[0119] In this embodiment, the finite field K whose characteristic p is 2, order q is 256, n is 30, and r is 25 multivariate equations is taken as an example. The certificate-free multivariate broadcast multi-signature method consists of the following steps:

[0120] A. Establish system parameters

[0121] (A1) The key generation center defines a finite field K with characteristic p and order q. In this embodiment, p is 2 and order q is 256.

[0122] (A2) The key generation center defines n-ary r multivariate equations on the finite field K. In this embodiment, n is 30 and r is 25.

[0123] P=(p 1 (x 1 ,x 2 ,···,x 30 ),···,p i (x 1 ,x 2 ,···,x 30 ),···,p 25 (x 1 ,x 2 ,···,x 30 ))

[0124] Each equation system p i is about the variable x being x1 、x 2 ,...,x 30 The nonlinear quadratic equation for , where i is 1, 2, ..., 25:

[0125]

[0126] Among them, each coefficient α, β, γ and variable x are in the finite field K.

[0127] (A3) The key generation cent...

Embodiment 3

[0168] In this embodiment, the finite field K whose characteristic p is 2, order q is 512, n is 42, and r is 24 multivariate equations is taken as an example. The multivariate broadcast multi-signature method based on no certificate consists of the following steps:

[0169] A. Establish system parameters

[0170] (A1) The key generation center defines a finite field K with feature p and order q. In this embodiment, p is 2 and order q is 512.

[0171] (A2) The key generation center defines n-ary r multivariate equations on the finite field K. In this embodiment, n is 42 and r is 24.

[0172] P=(p 1 (x 1 ,x 2 ,···,x 42 ),···,p i (x 1 ,x 2 ,···,x 42 ),···,p 24 (x 1 ,x 2 ,···,x 42 ))

[0173] Each equation system p i is about the variable x being x 1 、x 2 ,...,x 42 The nonlinear quadratic equation for , where i is 1, 2, ..., 24:

[0174]

[0175] Among them, each coefficient α, β, γ and variable x are in the finite field K.

[0176] (A3) The key generation ce...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

A multi-variable broadcast multi-signature method based on no certificate, which consists of establishing system parameters, generating partial keys, generating signature keys, signing, and verifying steps. The present invention combines the certificateless public key cryptosystem and the broadcast multi-signature technology under the multivariable public key cryptosystem, and proposes a certificateless multivariable broadcast multisignature method, which solves the problems of the identity-based public key cryptosystem Key escrow issues. The final multi-signature length of the present invention has nothing to do with the number of signers, and the verification time of the multi-signature is consistent with the verification time of a single part of the signature. It has the advantages of small signature and verification calculations, and is resistant to quantum computing attacks. It can be used in vehicle networks, education, etc. systems and other fields.

Description

technical field [0001] The invention belongs to the technical field of network information security, and specifically relates to cryptography or a multivariable public key cryptosystem or a certificateless public key cryptosystem or a broadcast multi-signature method. Background technique [0002] Multi-signatures are divided into ordered multi-signatures and broadcast multi-signatures according to the order of signatures. It can realize multiple users to sign and authenticate the same electronic file. At present, most broadcast multi-signatures are based on traditional public key cryptosystems, and their security is mainly based on the intractability of large integer decomposition problems or discrete logarithm problems. The emergence of quantum algorithms and the imminent birth of quantum computers will pose a threat to the broadcast multi-signature method based on traditional public key cryptography, and the identity-based broadcast multi-signature method has key escrow p...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Patents(China)
IPC IPC(8): H04L9/08
CPCH04L9/0825
Inventor 俞惠芳付帅凤
Owner XIAN UNIV OF POSTS & TELECOMM
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com