Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

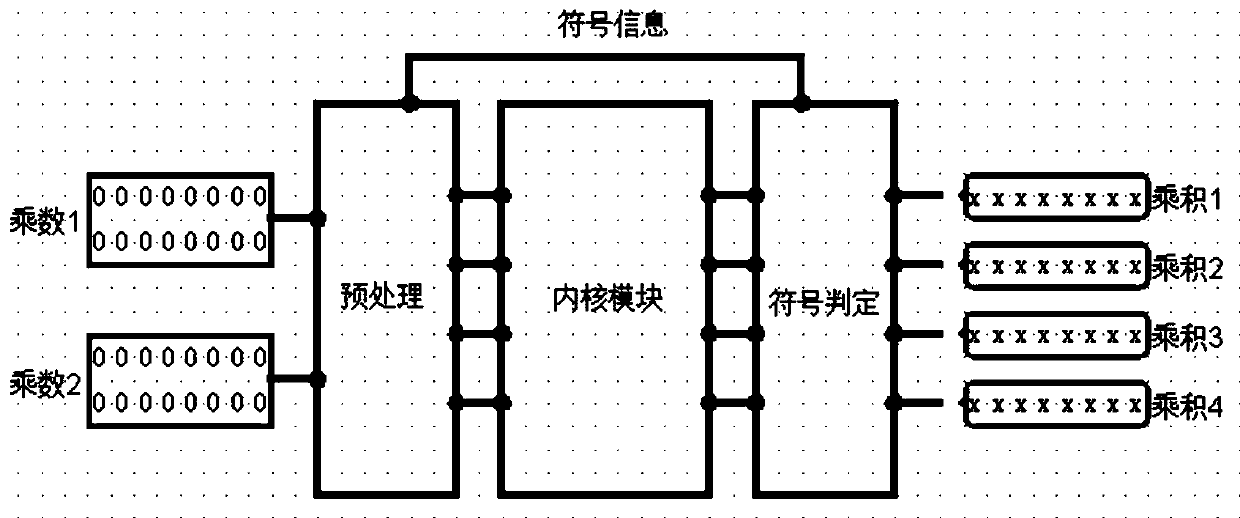
Data conversion method, multiplier, adder, terminal device and storage medium

A conversion method and adder technology, applied in the direction of electrical digital data processing, digital data processing parts, calculations using non-contact manufacturing equipment, etc., can solve problems such as over-design, achieve low power consumption, reduce computing overhead, low cost effect

Active Publication Date: 2020-03-17
JIMEI UNIV
View PDF10 Cites 3 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

Correspondingly, for deep learning algorithms based on convolutional neural networks, there is a possibility of "over-design" in the adder and multiplier designed for the IEEE-754 floating-point data format

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Data conversion method, multiplier, adder, terminal device and storage medium
  • Data conversion method, multiplier, adder, terminal device and storage medium
  • Data conversion method, multiplier, adder, terminal device and storage medium

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

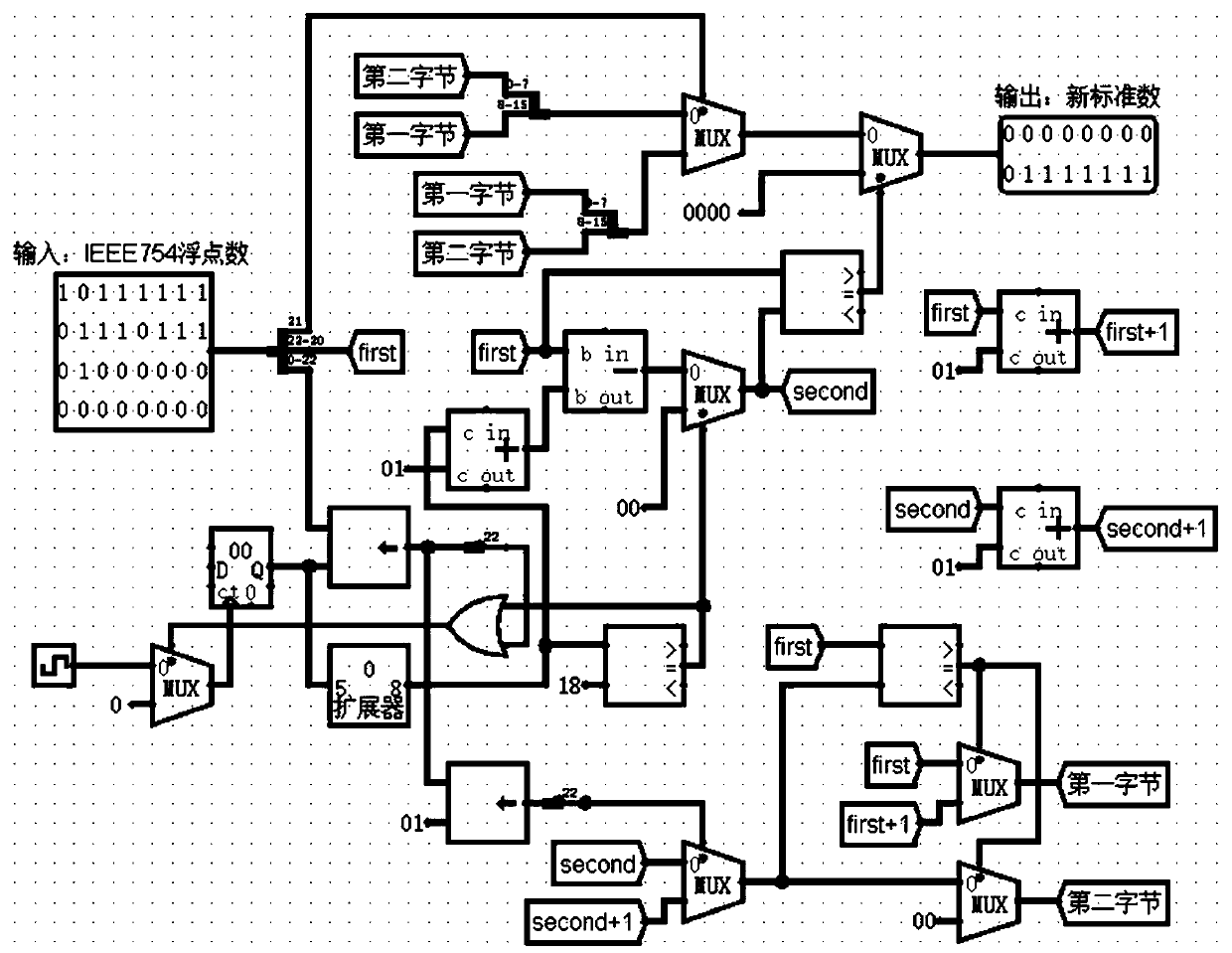
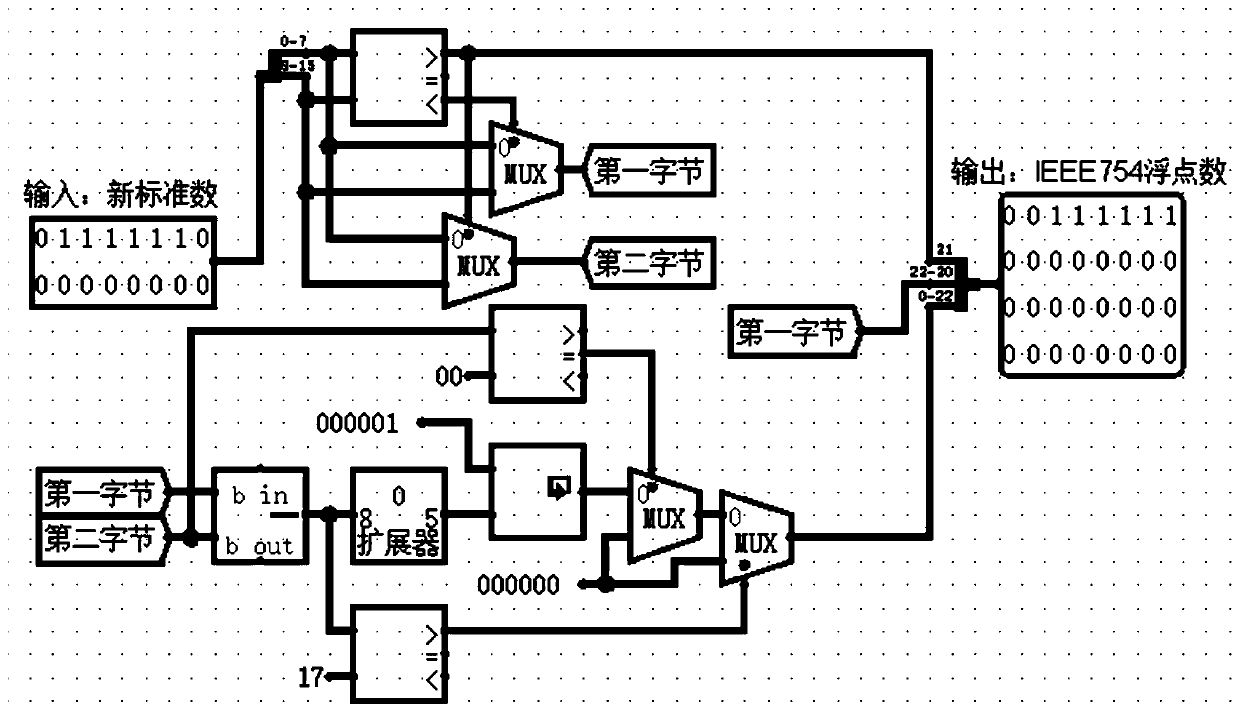
[0056] An embodiment of the present invention provides a data conversion method for image recognition based on a convolutional neural network model, which is used to extract key features from images or videos input by the network through a convolutional neural network, so as to classify images or detect objects . Since the convolution operation is usually the most expensive function in the convolutional neural network, and the multiplication operation is the most expensive step in the convolution operation, therefore, the data conversion method proposed in this embodiment will be used for the convolution operation. Operations are performed after the points are converted to the new standard number format.

[0057] The specific conversion method is as follows:

[0058] 1. The floating-point number F uses k n-bit (bit) integer numbers (a 1 ,a 2 ,a 3 ...a k ) to approximate the sequence, the specific mathematical meaning is expressed as:

[0059] (1) Through this data form...

example 1

[0078] Let’s take the floating point number -0.96582 as an example to illustrate, its IEEE754 format is: 10111111011101110100000000000000, a total of 32 bits, counting from right to left, the 32nd bit represents the sign bit of the original floating point number, 1 represents a negative number, 0 represents a positive number, this implementation In the example, if the 32nd bit is 1, the original floating-point number is a negative number. A total of 8 bits from the 24th to the 31st bits represent the exponent code of the original floating point number. The 1st to 23rd digits represent the mantissa of the original floating-point number with a total of 23 digits. Therefore, the exponent code of the floating point number -0.96582 is 01111110, and the mantissa is 11101110100000000000000.

[0079] (1): The floating point number -0.96582 is non-zero;

[0080] (2): Set the first byte a 1 Equal to the order code 01111110, set count=1;

[0081] (3): The mantissa of the original flo...

example 2

[0090] The following takes the floating point number 0.5 as an example for illustration, and its IEEE754 format is:

[0091] 0 01111110 00000000000000000000000

[0092] The sign bit is 0, the exponent code is 01111110, and the mantissa is 00000000000000000000000.

[0093] (1): The floating point number 0.5 is not zero;

[0094] (2): Set the first byte a 1 Equal to the order code 01111110, set count=1;

[0095] (3): the 24th-count=23rd bit of the mantissa is not equal to 1;

[0096] (4): count=23 is not established;

[0097] (5): set count=count+1=1+1=2;

[0098] (6): the 24th-count=22 bit of the mantissa is not equal to 1;

[0099] ……..

[0100] (46): count=23 is established, the second byte a will be set 2 =00000000;

[0101] (47): The sign bit is 0, set the first byte a 1 Placed in the high 8 bits, the second byte a 2 Put in the lower 8 bits;

[0102] The floating point number 0.5 in the new standard format is: 01111110 00000000, its mathematical meaning is 0.5, an...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention relates to a data conversion method, a multiplier, an adder, terminal equipment and a storage medium. The method comprises the following steps: inputting a floating-point number F; converting the input floating-point number F according to the following conversion rules: a formula (shown in the description), ai is an integer number, each integer number is n bits, i is a serial number,and k is the number of integer numbers; according to the converted floating-point number F, setting the converted new standard number as a number formed by arranging k integer numbers ai of n bits from high to low in a descending order or ascending order; when the floating-point number F is equal to 0, enabling the k integer numbers of n bits to be all negative infinity; and outputting the converted new standard number. According to the method, the advantage of large numerical representation range of the single-precision floating-point number is reserved, and the calculation overhead of the floating-point number multiplication operation is reduced, so that the calculation overhead of the deep neural network algorithm can be reduced, and a solution is provided for the deployment of the deep neural network algorithm on low-cost and low-power equipment.

Description

technical field [0001] The invention relates to the technical field of data conversion, in particular to a data conversion method, a multiplier, an adder, a terminal device and a storage medium. Background technique [0002] Deep neural network algorithms with image recognition and natural language processing as their main applications are becoming more and more popular in the social economy. Deep neural networks have high requirements on the computing performance of computing devices. How to reduce the computing overhead of algorithms has become a common concern of both academia and industry. [0003] In recent years, deep learning algorithms based on convolutional neural networks have achieved impressive results in fields such as machine vision and natural language processing. The convolutional neural network extracts key features from pictures or videos through complex neural network design and increases the depth of the neural network, and finally realizes the classific...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): G06F7/50G06F7/523G06F7/57G06N3/04
CPCG06F7/523G06F7/50G06F7/57G06N3/045
Inventor 黄斌叶从容蔡国榕陈豪郭晓曦
Owner JIMEI UNIV
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com