Supercharge Your Innovation With Domain-Expert AI Agents!

A detection method for subsynchronous oscillation in power system with high proportion of renewable energy

A renewable energy, sub-synchronous oscillation technology, applied in the field of power system, can solve the problems of not ideal frequency signal processing, excessive calculation amount, etc., and achieve the effects of accurate extraction, improved calculation accuracy, and good robustness.

Active Publication Date: 2021-03-30
UNIV OF ELECTRONIC SCI & TECH OF CHINA +1
View PDF6 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

But it is not ideal for the processing of emphasized frequency signals, D.-H
Pham and S. Meignen proposed higher order SST levels to achieve better results, but the increase in order brings more calculations

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • A detection method for subsynchronous oscillation in power system with high proportion of renewable energy
  • A detection method for subsynchronous oscillation in power system with high proportion of renewable energy
  • A detection method for subsynchronous oscillation in power system with high proportion of renewable energy

Examples

Experimental program
Comparison scheme
Effect test

Embodiment

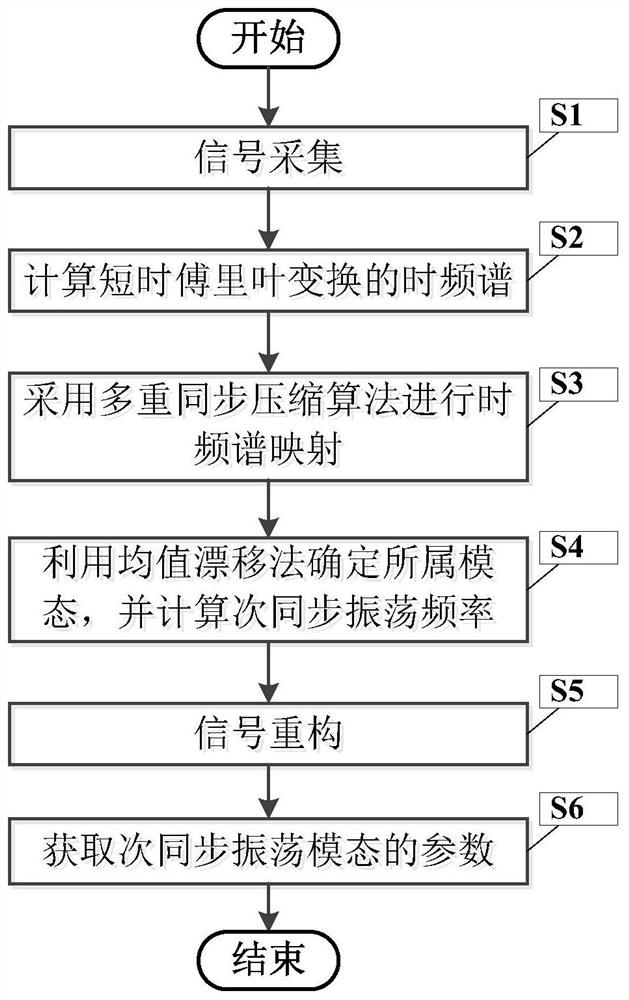
[0067] figure 1 It is a flowchart of a method for detecting subsynchronous oscillation of a high-proportion renewable energy power system according to the present invention.

[0068] In this example, if figure 1 As shown, the present invention is a method for detecting subsynchronous oscillation of a high-proportion renewable energy power system, comprising the following steps:

[0069] S1, signal acquisition;

[0070] Collect the voltage signal or current signal at the output end of the high-proportion renewable energy power system;

[0071] S2. Calculate the time spectrum of the short-time Fourier transform of the voltage signal or the current signal;

[0072] S2.1. Let the time-varying signal model of voltage signal or current signal be s(t):

[0073] s(t)=A(t)e iφ(t) (1)

[0074] Among them, A(t) represents the amplitude of the voltage signal or current signal, φ(t) represents the phase of the voltage signal or current signal, i is the imaginary number unit, and t i...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a detection method for subsynchronous oscillation of a high-proportion renewable energy power system. Firstly, the voltage signal or current signal at the output end of the high-proportion renewable energy power system is collected, and then the short-time Fourier transform of the voltage signal or current signal is calculated. Transformed time-spectrum, and use the multiple synchronous compression algorithm to map the short-time Fourier transform time-spectrum to a new time-spectrum, and then use the mean shift method to determine the mode of the coefficient after multiple synchronous compression transformation higher than the set threshold, The frequency of subsynchronous oscillation is calculated, and finally the signal of the subsynchronous oscillation mode is reconstructed and the least square estimation method is used to estimate the parameters of each subsynchronous oscillation mode.

Description

technical field [0001] The invention belongs to the technical field of power systems, and more specifically, relates to a detection method for subsynchronous oscillation of a high-proportion renewable energy power system. Background technique [0002] Subsynchronous oscillation (SSO) is an anomaly caused by the interaction between a converter-based generator and the grid of a power system. With the continuous development of environmental pollution and energy crisis, the penetration and application of renewable energy (especially wind energy and photovoltaic power generation) has been increasing, but at the same time, many SSO incidents have been triggered. During these incidents, SSO becomes so destructive that it threatens the security of the equipment and the stable operation of the system. [0003] Today, synchronous measurement techniques including wide area measurement system (WAMS) and phasor measurement unit (PMU) have covered most transmission networks and power pla...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): G01R23/02G01R31/08H02J3/00
CPCG01R23/02G01R31/086G01R31/088H02J3/00
Inventor 蔡东升黄琦马钺宫彦张锋亢朋朋王衡樊国伟
Owner UNIV OF ELECTRONIC SCI & TECH OF CHINA
Features
  • R&D
  • Intellectual Property
  • Life Sciences
  • Materials
  • Tech Scout
Why Patsnap Eureka
  • Unparalleled Data Quality
  • Higher Quality Content
  • 60% Fewer Hallucinations
Social media
Patsnap Eureka Blog
Learn More

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com