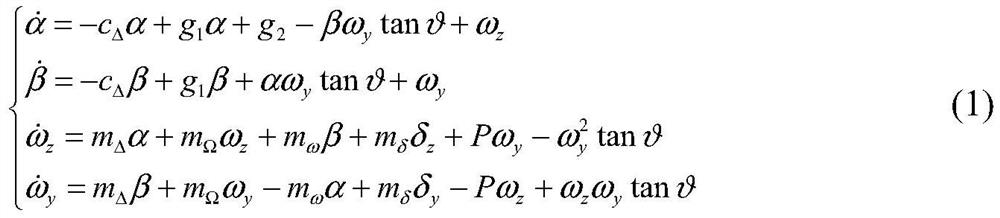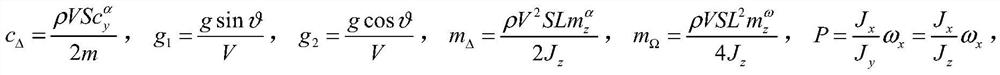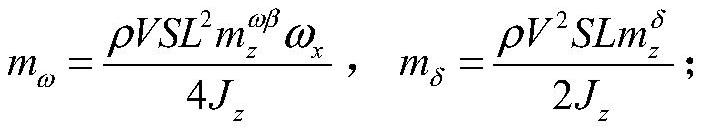An Analysis Method of Geometric Nonlinear Lower Angular Motion Characteristics of Double Spinning Projectiles
A technique of geometric nonlinearity and characteristic analysis, which is applied in the field of double-spin angular motion characteristic analysis, and can solve the problems of nonlinear motion phenomena, which are difficult to theoretical analysis and interpretation of linear systems.
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
Image
Examples
Embodiment Construction
[0063] Examples are given below to describe the present invention in detail.
[0064] This embodiment provides a method for analyzing the geometric nonlinear lower angular motion characteristics of a dual-rotor projectile. Taking the deflection angle of the yaw rudder as a bifurcation parameter, the boundary conditions for the dynamic instability of the dual-rotor projectile are given, and the angle at the critical point is determined. For the bifurcation phenomenon caused by motion, the central manifold theorem is used to reduce the dimensionality of the angular motion near the bifurcation point. Through the reduction and analysis of the equation, the variation law of the equilibrium state near the bifurcation point is obtained.
[0065] The analysis method mainly includes the following steps:
[0066] Step 1: Establish the angle of attack α, sideslip angle β, and pitch angular velocity ω of the double-spin projectile z , yaw angular velocity ω y The nonlinear angular equat...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com