Supercharge Your Innovation With Domain-Expert AI Agents!

A collaborative signature method, device and system based on elliptic curve

An elliptic curve and signature device technology, applied in the field of information security, can solve the problems of large amount of communication data, large computational overhead, and many times of communication, and achieve the effects of simple communication interaction, convenient algorithm implementation, and security assurance.

Active Publication Date: 2022-02-11
ZHENGZHOU XINDA JIEAN INFORMATION TECH
View PDF7 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

In addition, in this scheme, the interaction between various entities is complex, involving multiple operations such as point addition, point multiplication, and point subtraction. The number of communications is large, the amount of communication data is large, and the calculation overhead is large.

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • A collaborative signature method, device and system based on elliptic curve
  • A collaborative signature method, device and system based on elliptic curve
  • A collaborative signature method, device and system based on elliptic curve

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

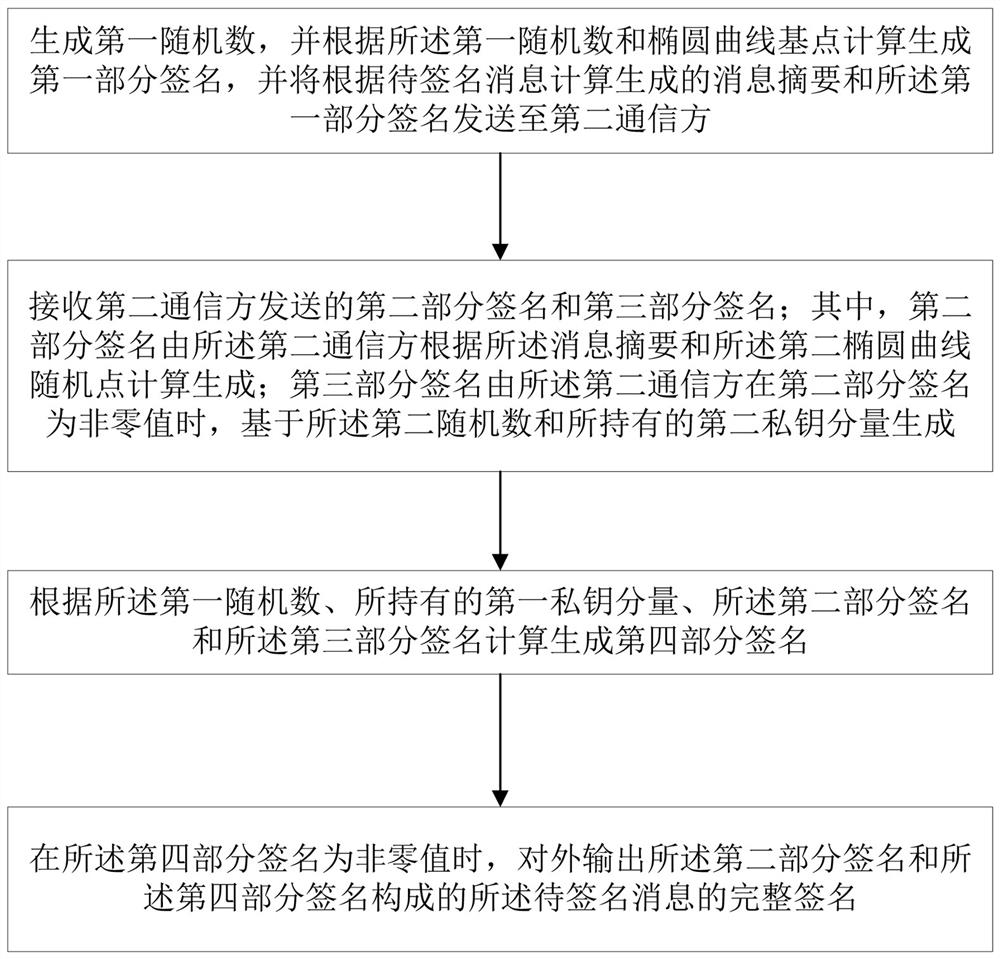
[0056] figure 1 is a flow chart of the elliptic curve-based collaborative signature method applied to the first communication party performing collaborative signature according to an embodiment of the present invention, as shown in figure 1 As shown, the collaborative signature method includes:

[0057] Step 101: Generate a first random number k, calculate and generate a first partial signature based on the first random number k and the base point of the elliptic curve, and send the message digest and the first partial signature to the second communication party, so that the second communication party can calculate and determine a second elliptic curve random point based on the generated second random number and the first partial signature;

[0058] Specifically, the point multiplication algorithm is used to calculate the first random number k 1 and elliptic curve base point G calculation to generate the first part of the signature [k 1 ] G;

[0059] Specifically, when gen...

Embodiment 2

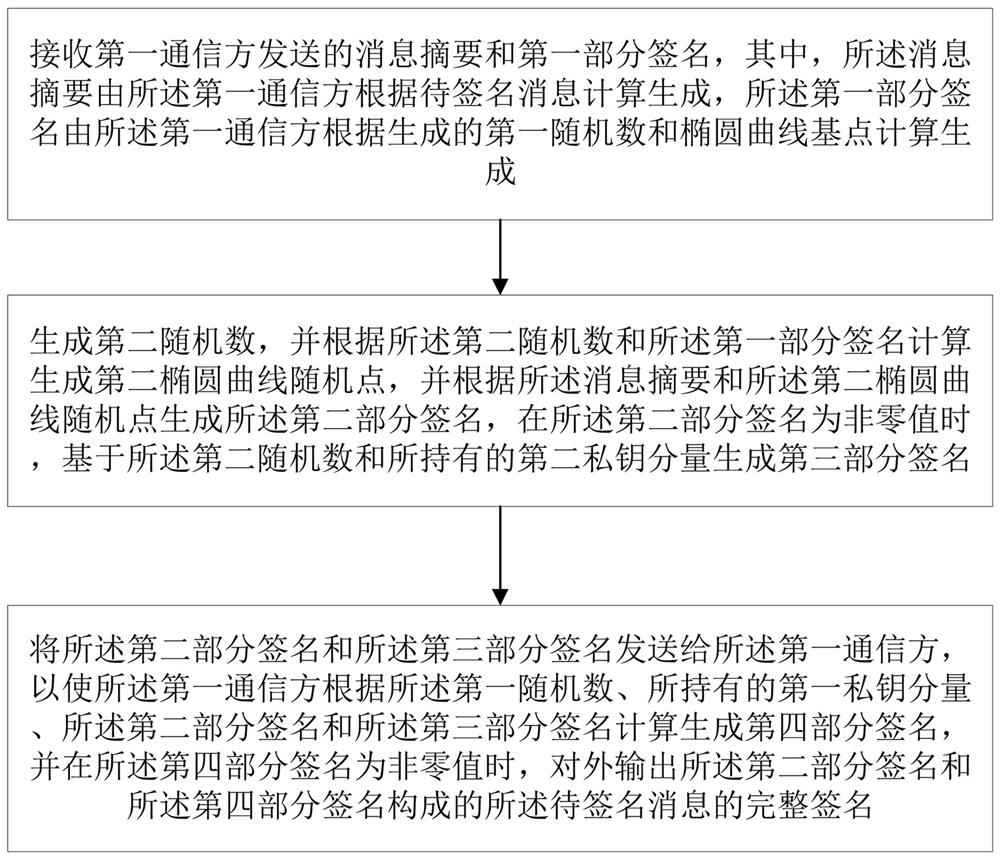
[0077] This embodiment describes the collaborative signature method from the perspective of the second communicating party, as image 3 As shown, the collaborative signature method includes:

[0078] Step 201, receiving a message digest and a first partial signature sent by the first communicating party, wherein the message digest is calculated and generated by the first communicating party based on the message to be signed, and the first partial signature is calculated by the first communicating party according to The first random number generated and the elliptic curve base point calculation generated.

[0079] Step 202, generating a second random number, and calculating and generating a second elliptic curve random point according to the second random number and the first partial signature, specifically, using the formula (x 1 ,y 1 )=[k 2 ][k 1 G] = [k 1 k 2 ] G calculates the second random number and the first partial signature to generate the second elliptic curve ...

Embodiment 3

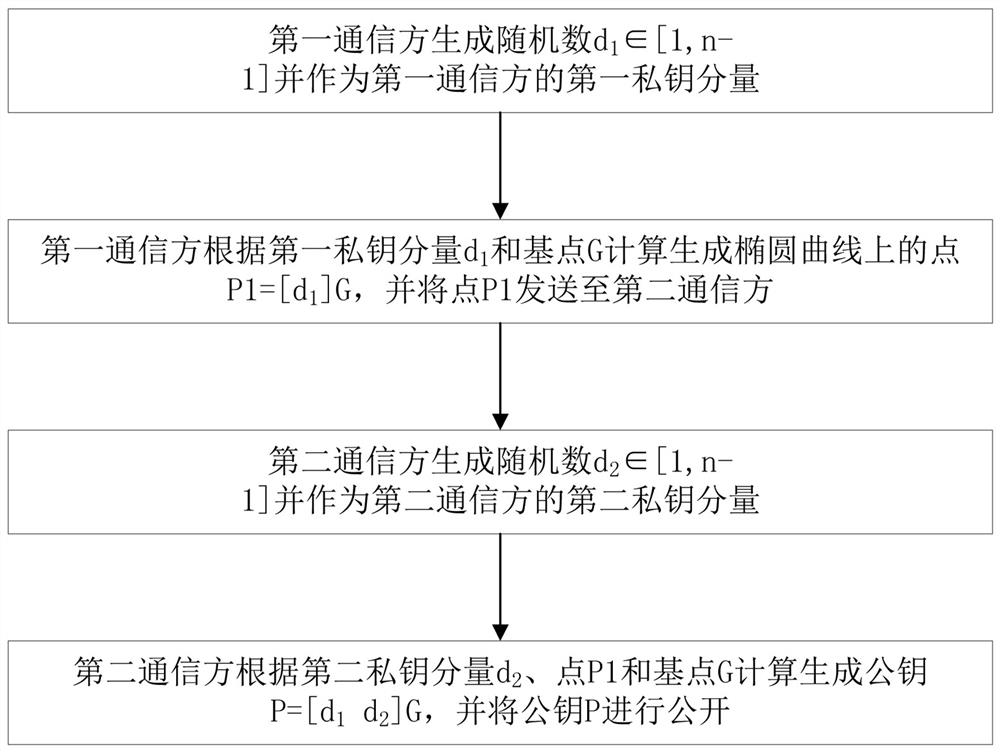
[0090] In order to enable those skilled in the art to understand the above collaborative signature process more clearly, as Figure 4 As shown, this embodiment describes in detail the process of interaction between the first communication party and the second communication party.

[0091] The collaborative signature process is as follows:

[0092] Step 301, the first communication party generates a first random number k 1 , and according to the first random number k 1 Calculate with the elliptic curve base point G to generate the first part of the signature; k 1 Obtained by one or more random number operations between [1,n-1], the operations include linear operations, multiplication, and inversion; G represents the n-order base point on the elliptic curve E, and the elliptic curve E is an elliptic curve defined over a finite field Fq.

[0093] During specific implementation, the first communication party adopts the dot product algorithm to calculate the first random number...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The present invention proposes a collaborative signature method, device and system based on elliptic curves. In the method, the key is generated: the two parties in the communication perform cooperative signature by calculating and exchanging partial signature information, random numbers, and message digests; in the present invention, the two parties in the communication store the Part of the private key information, the two parties cooperate to complete the signature of the message, neither party can obtain the complete private key information, which improves the security of the private key; and in the signature generation process, the first communication party needs to carry out the calculation of the first part of the signature A dot multiplication operation, and the dot multiplication operation supports pre-computation; the second communication party needs to perform a dot multiplication operation when calculating the second elliptic curve random point, and the dot multiplication operation supports pre-computation, so the entire collaborative signature process requires The calculation overhead of the algorithm is significantly reduced, which makes the communication interaction simple and the amount of communication data is reduced, which brings great convenience to the realization of the algorithm.

Description

technical field [0001] The present invention relates to the technical field of information security, in particular to a collaborative signature method, device and system based on elliptic curves. Background technique [0002] In terms of information security, digital signature is a very important part. Secure digital signatures determine the identity of the other party in applications such as electronic documents and electronic contracts, and are the basis for authentic information. In the public key cryptosystem, ensuring the security of the private key is a very important issue. The user's private key usually needs to be safely stored and used in a special hardware security module (HSM, Hardware Security Module), and the private key cannot be derived from the cryptographic hardware. Common HSMs include USBKEY (U-shield), smart card, TF card (Trans-flash Card, flash memory card), password chip, etc. [0003] Currently, there are various schemes aimed at improving the sec...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Patents(China)
IPC IPC(8): G06F21/64G06F21/46
CPCG06F21/64G06F21/46
Inventor 雷宗华彭金辉孙晓鹏廖正赟李鑫
Owner ZHENGZHOU XINDA JIEAN INFORMATION TECH
Features
  • R&D
  • Intellectual Property
  • Life Sciences
  • Materials
  • Tech Scout
Why Patsnap Eureka
  • Unparalleled Data Quality
  • Higher Quality Content
  • 60% Fewer Hallucinations
Social media
Patsnap Eureka Blog
Learn More

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com