Secure multi-party quantum computing method based on quantum Fourier transform
A technology of Fourier transform and quantum computing, which is applied in the field of quantum computing, can solve problems such as difficulty in realization, leakage of secret numbers, and many quantum resources, and achieve practical significance, make up for security loopholes, and be simple to operate
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
Image
Examples
Embodiment Construction
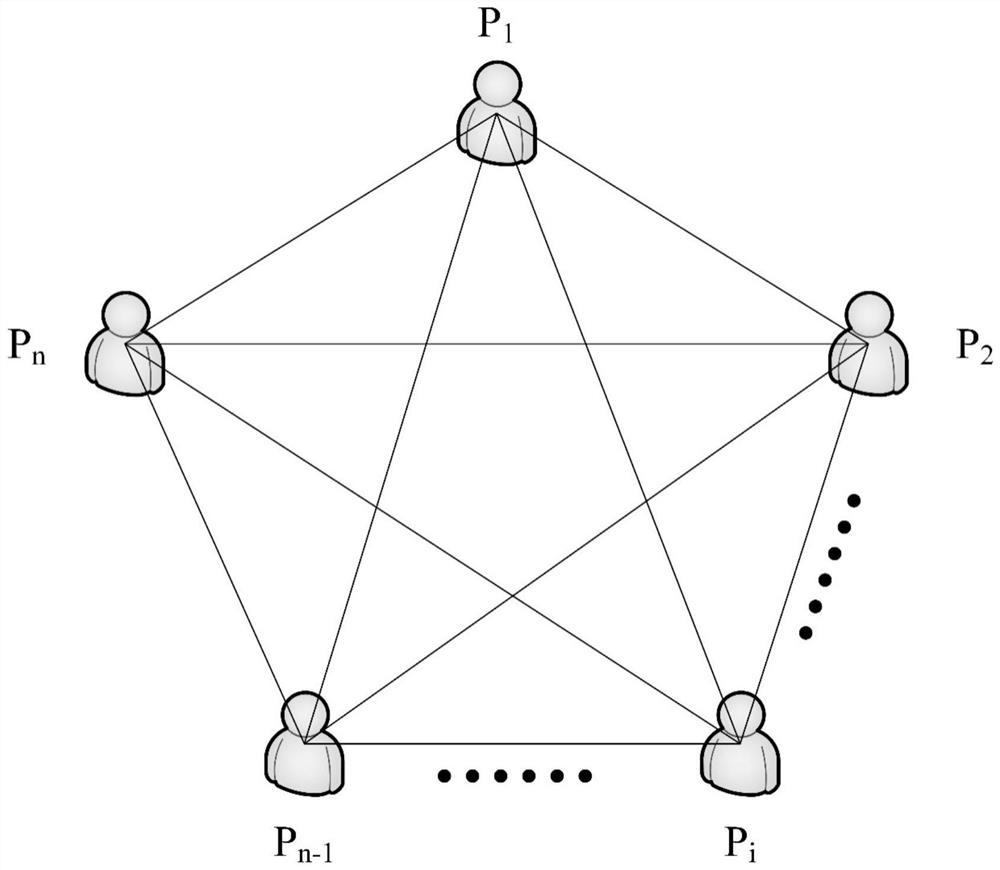
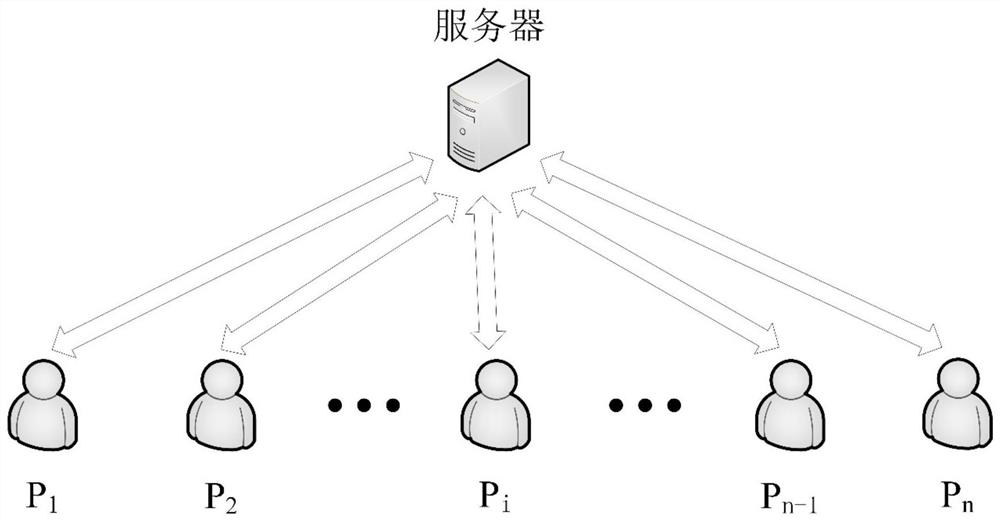
[0023] In order to make those skilled in the art better understand the solutions of the embodiments of the present invention, the following is combined with the following appendixes. Figure 1-3 The embodiments of the present invention will be further described in detail with reference to the implementation manner. Embodiment 1 of the present invention provides a method for realizing secure multi-party quantum computing, including a server and n clients P 1 , P 2 ,...,P n , client P i Each has a secret number x i , where x i ∈ {0,1,...,N}, i=1,...,n.
[0024] as attached figure 1 As shown, n clients jointly construct N+1 blinding matrices B 0 , B 1 ,…,B N , for each blinding matrix B j , j=0,1,...,N. Client P i Build its i-th row element, which is P i Randomly generate n positive integers as matrix B j The i-th row element of , and satisfy Blind Matrix B j The form is as follows:
[0025]
[0026] for matrix B j The i-th row element of If t=i, then th...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com