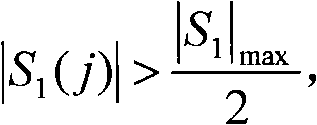Method for synthesis and reconstruction of output signal of quadrature coil of MRI (magnetic resonance imaging) system

A technology of output signals and quadrature coils, which is applied in the field of synthesis and reconstruction of quadrature coil output signals in MRI systems, can solve problems such as inflexibility and inability to obtain synthesis effects, and achieve ideal image effects

Active Publication Date: 2011-05-25
鑫高益医疗设备股份有限公司
View PDF5 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

This method is relatively rigid. When the actual phase difference between the two sign

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Method for synthesis and reconstruction of output signal of quadrature coil of MRI (magnetic resonance imaging) system
  • Method for synthesis and reconstruction of output signal of quadrature coil of MRI (magnetic resonance imaging) system
  • Method for synthesis and reconstruction of output signal of quadrature coil of MRI (magnetic resonance imaging) system

Examples

Experimental program
Comparison scheme
Effect test

Example Embodiment

[0034] The present invention will be described in further detail below in conjunction with the embodiments of the drawings.

[0035] See figure 1 The method for synthesizing and reconstructing output signals of quadrature coils in the MRI system includes the following six steps:

[0036] Step 1. Collect the two output signals of the quadrature coil in the MRI system:

[0037] The orthogonal coils in the MRI system are marked as I and Q respectively, and the magnetic resonance signals induced by the I and Q of the orthogonal coils are amplified and collected by their respective receivers to obtain the I circuits of the orthogonal coils. The original output signal S 1 And the original output signal S of the quadrature coil Q 2 ;

[0038] I original output signal S 1 And Q original output signal S 2 Both are a two-dimensional data set. If the magnetic resonance signal obtained by the respective receiver contains n layers, then the original output signal S 1 It is a two-dimensional signa...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to view more

PUM

No PUM Login to view more

Abstract

The present invention relates to a method for synthesis and reconstruction of output signals of a quadrature coil of an MRI (magnetic resonance imaging) system, which is characterized by comprising the following steps: 1, collecting two paths of output signals of the quadrature coil of the MRI system; 2, screening the original output signals S1 and S2 of the path I and the path Q of the quadrature coil and eliminating gain overflow layers; 2, analyzing first signals and finding out the position of maximum signal data in the first signals; 4, finding out the range of full width at half maximum of signal data with a maximum magnitude in the first signals; 5, respectively calculating phase differences of the signal data of the first signals and second signals at each point within the range of the full width at half maximum obtained in the further step, and averaging the phase differences to obtain a final phase difference; and 6, obtaining a final image through synthesizing and reconstructing the original output signals of the path I and the original output signals of the path Q by adopting the final phase difference obtained in the fifth step. Compared with the prior art, the image synthesized and reconstructed in the method has ideal quality.

Description

technical field [0001] The invention relates to a method for synthesizing and reconstructing output signals of quadrature coils in an MRI system. Background technique [0002] Magnetic Resonance Imaging (MRI for short) is a high-tech in medical imaging. It uses magnetic field and radio frequency pulses to make hydrogen nuclear resonance in the living body generate signals, which are processed by computer to form images. Since it came out in the 1970s, MRI technology has developed rapidly. Due to its high resolution, multiple imaging parameters, tomographic imaging at any level, and no ionizing radiation, it has become one of the most advanced tools in imaging examinations. Widely used in clinical examination of various systems of the human body. In 2003, Paul C. Lauterbur and Peter Mansfield, who invented magnetic resonance imaging, were awarded the Nobel Prize in Physiology or Medicine. [0003] When quadrature coils are used to improve the performance of the receiving ch...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to view more

Application Information

Patent Timeline
no application Login to view more
IPC IPC(8): G01R33/54
Inventor 朱剑锋吴环
Owner 鑫高益医疗设备股份有限公司
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Try Eureka
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap