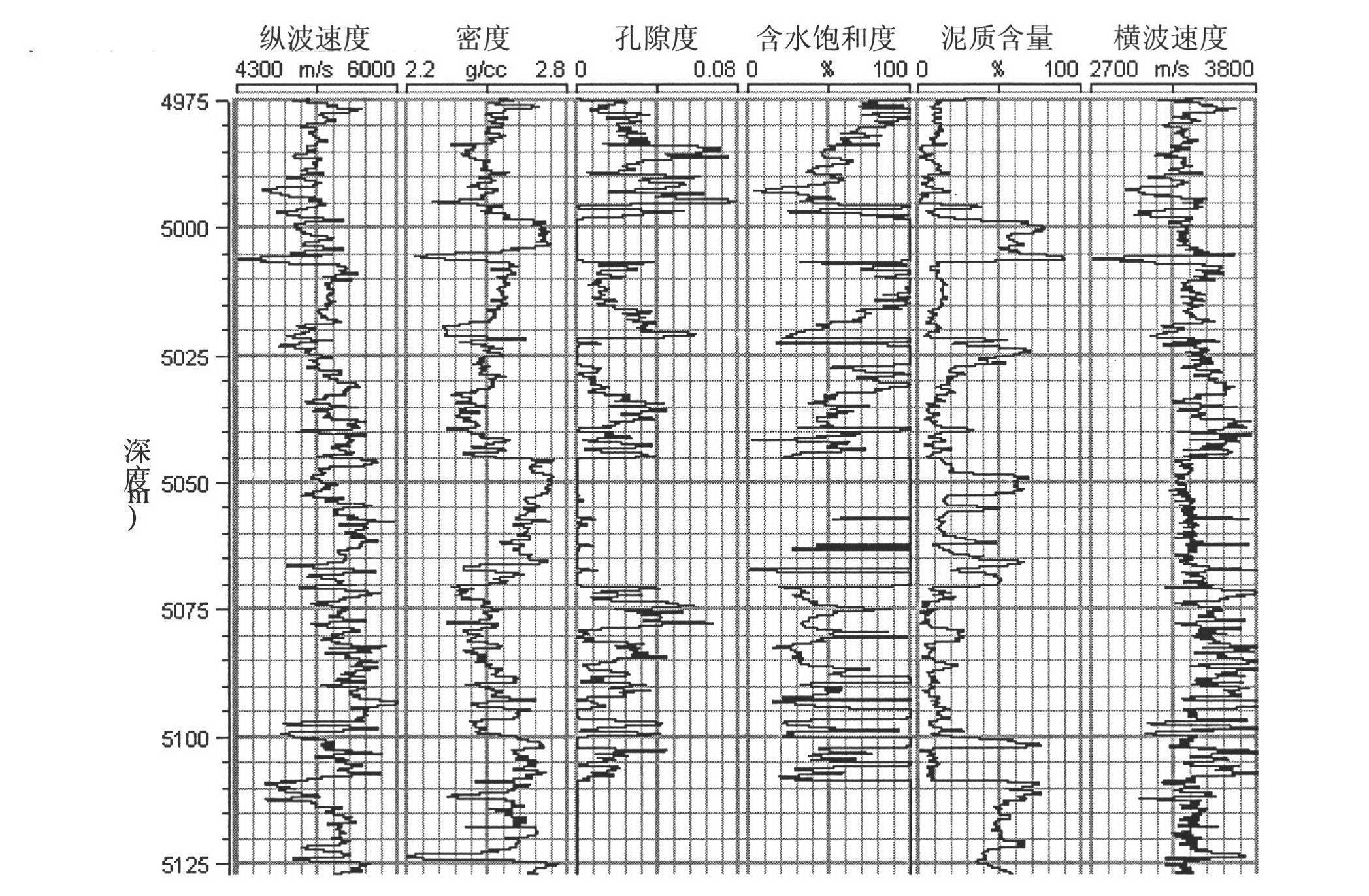
Method for estimating velocity of transverse waves based on inversion of equivalent elastic modulus for self-adapting matrix minerals
A technology of shear wave velocity and self-adaptation, which is applied in the fields of seismology and seismic signal processing for well logging records. It can solve the problems of large elastic modulus value variation range, high cost, and difficult setting, and achieve high calculation accuracy. , reduce multi-solution, and reduce the number of effects
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
Image
Examples
Embodiment Construction
[0017] The shear wave velocity estimation method based on the inversion of the equivalent elastic modulus of the adaptive matrix mineral, the specific implementation steps are as follows:
[0018] (1) Taking a single logging depth point as the research object, according to the logging data (P-wave velocity, density and porosity) at this depth point, the empirical relationship between P-wave velocity and S-wave velocity of sand and mudstone (Castagna, 1993) is used to estimate Initial shear wave velocity, and calculate the value range, initial value and increment of Poisson's ratio of dry rock and equivalent bulk modulus of matrix mineral at the logging depth point.
[0019] The empirical relationship between P-wave velocity and S-wave velocity of sand-mudstone (Castagna, 1993) is shown in Equation 1,
[0020] V s =0.804V p -0.856 (1)
[0021] where V p represents the longitudinal wave velocity, V s represents the shear wave velocity.
[0022] Poisson's ratio of dry rock ...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com