Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

A Spectrum Detection Method Based on Compressive Sensing under Blind Sparse Condition

A compressed sensing and spectrum detection technology, applied in electrical components, transmission monitoring, transmission systems, etc., can solve the problems of slow detection algorithm convergence speed, increased algorithm complexity, missed spectrum detection, etc., to achieve convergence, real-time The effect of good performance and low complexity

Inactive Publication Date: 2016-02-03
HARBIN INST OF TECH
View PDF4 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

In addition, in general, unlicensed users (SUs) often do not know the signal information of authorized users (PUs), and traditional algorithms require prior information on signal sparsity
Under the premise that the sparsity is unknown, if the traditional algorithm estimates the signal sparsity too high, the convergence speed of the detection algorithm will slow down, and the complexity of the algorithm will increase; if the signal sparsity is too low, it will occur Spectrum Missing
At present, there is no detailed research using the relevant knowledge of compressed sensing to detect frequency bands under the condition of blind sparsity

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • A Spectrum Detection Method Based on Compressive Sensing under Blind Sparse Condition
  • A Spectrum Detection Method Based on Compressive Sensing under Blind Sparse Condition
  • A Spectrum Detection Method Based on Compressive Sensing under Blind Sparse Condition

Examples

Experimental program
Comparison scheme
Effect test

specific Embodiment approach 1

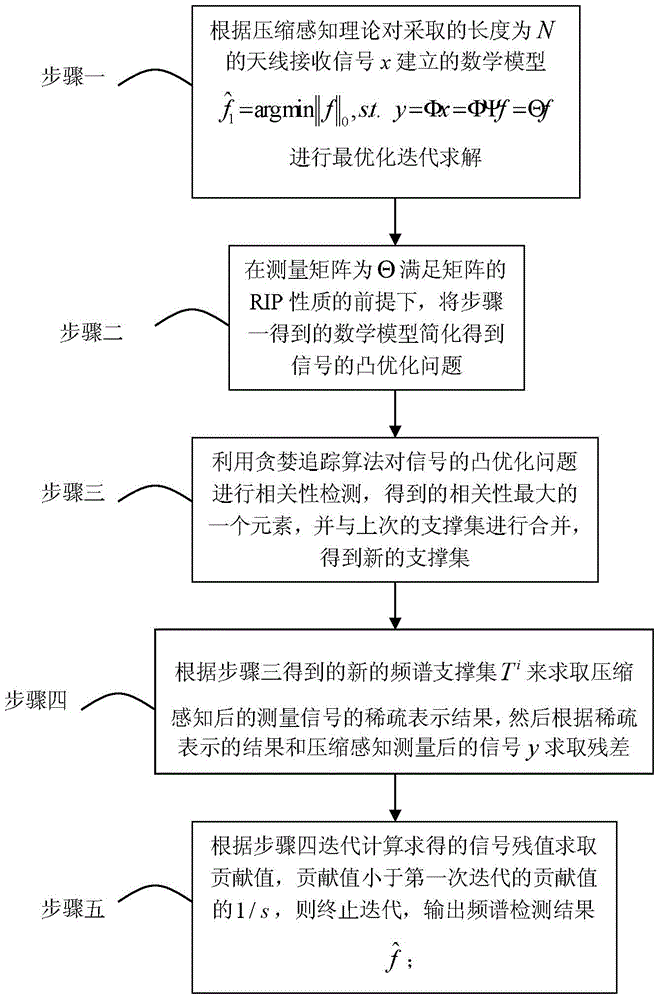
[0029] Specific implementation mode 1: A spectrum detection method for compressive sensing under blind sparse conditions in this implementation mode is specifically prepared according to the following steps:

[0030] Step 1. According to the compressive sensing theory, a mathematical model is established for the antenna receiving signal x with a length of N Carry out optimization iterative solution; Wherein, measurement matrix is ​​Θ, and the signal after compressed sampling is y, and f is the sparse base coefficient sought, Ψ is transformation base matrix, and Φ is Gaussian random matrix;

[0031] Step 2, under the premise that the measurement matrix is ​​Θ satisfying the RIP property of the matrix, the mathematical model obtained in step 1 is simplified to obtain the convex optimization problem of the signal;

[0032] Step 3: Use the greedy pursuit algorithm to detect the correlation of the convex optimization problem of the signal, and obtain an element with the greatest c...

specific Embodiment approach 2

[0042] Specific embodiment 2: The difference between this embodiment and specific embodiment 1 is: in step 1, according to the compressed sensing theory, the mathematical model established by the antenna receiving signal x with a length of N The specific problem for optimization iterative solution is described as follows:

[0043] (1) The length of the signal received by the antenna is N, and the compressed sampling rate is Randomly select K sub-frequency bands from N frequency bands as frequency bands occupied by authorized users, and M is the number of compressed sampling points;

[0044] (2) The N×1-dimensional noise-free signal x_o obtained by the inverse Fourier transform of the frequency band occupied by authorized users; x_o∈R N , the method of inverse Fourier transform is x_o=Ψf, f is the sparse basis coefficient sought;

[0045] (3) If there are only K elements in f that are non-zero, the signal x_o is said to be sparse under the transformation basis of Ψ, and the...

specific Embodiment approach 3

[0053] Specific embodiment three: the difference between this embodiment and specific embodiment one or two is that in step two, under the premise that the measurement matrix is ​​Θ satisfying the RIP property of the matrix, the mathematical model obtained in step one is simplified to obtain the convex optimization problem of the signal The specific process is:

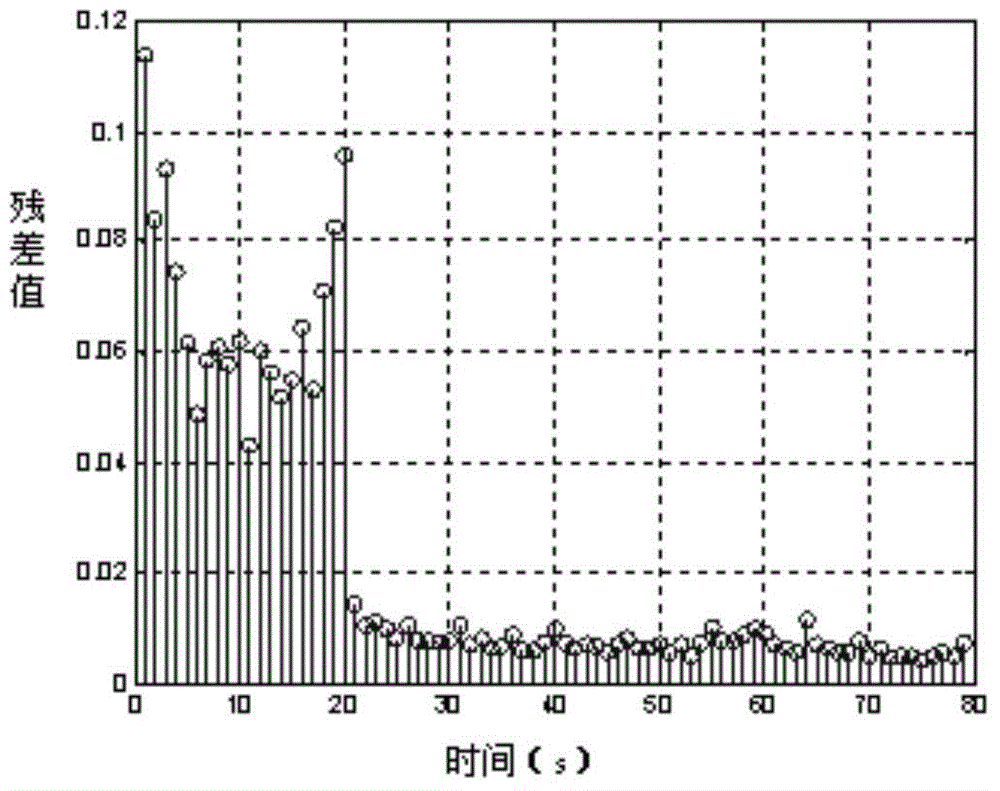
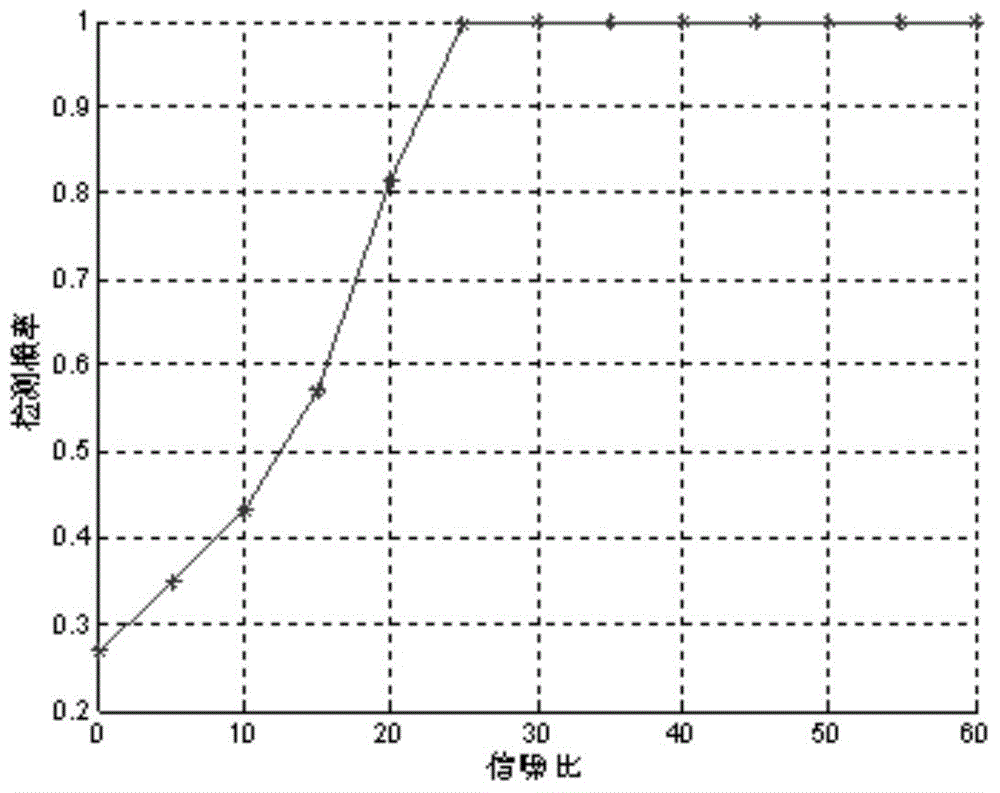
[0054] Although the 0-norm algorithm of compressed sensing is optimal, it is an NP-hard problem. In order to find the sparsest solution, it is necessary to exhaustively This is a possibility, and the complexity of the algorithm is extremely high; relevant data show that under the premise that the measurement matrix is ​​Θ and satisfies the RIP property of the matrix, use MATLAB software as the simulation software, input: sampling vector y, measurement matrix Θ=ΦΨ of compressed sensing, iteration The termination threshold s, the purpose of the algorithm in the invention is to output the spectrum sensing result under t...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention provides a compressed sensing spectrum detecting method under the blind sparse condition. The aim of spectrum detecting under the condition that the sparseness is unknown is achieved. The compressed sensing spectrum detecting method under the blind sparse condition includes the steps of (1) conducting optimization iteration solving on a built mathematic model (please see the specifications for the formula), (2) conducting simplification to obtain convex optimization problem of reconstitution signals, (3) obtaining an element with the maximum correlation, merging the element with a support set of last-time iteration, and obtaining a new support set, (4) obtaining a residual error, (5) obtaining a contribution value and outputting spectrum detecting results (please see the specifications for the formula) and the like. The mode is applied to the compressed sensing spectrum detecting method.

Description

technical field [0001] The invention relates to a frequency spectrum detection method of compressed sensing under the condition of blind sparseness. Background technique [0002] Spectrum is a precious resource for wireless communications. With the increasing demand of users for high-speed data services, the demand for spectrum resources in communication systems is also increasing, and spectrum resources are increasingly scarce. In order to improve the utilization of spectrum resources and meet the needs of users for high-speed data transmission, cognitive radio technology emerges as the times require. Cognitive radio can utilize spectrum holes for data transmission of unlicensed users (SUs) without affecting data transmissions of authorized users (PUs). [0003] According to the Nyquist sampling law, in the conversion process from analog to digital, in order not to lose information, it must be sampled at a sampling rate at least twice the highest frequency of the signal to...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Patents(China)
IPC IPC(8): H04B17/30H04B17/382
Inventor 高玉龙张蔚马永奎朱尤祥张中兆陈艳平
Owner HARBIN INST OF TECH
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com