Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Space rendezvous system gain scheduling control method with linearization errors taken into consideration

A technology of gain scheduling control and space rendezvous, which is applied in the direction of adaptive control, general control system, control/regulation system, etc., and can solve the time-consuming problems of spacecraft orbit rendezvous missions, etc.

Active Publication Date: 2014-10-01
哈尔滨工业大学人工智能研究院有限公司
View PDF5 Cites 11 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0005] In order to solve the problem that the control method of the existing spacecraft orbit rendezvous system ignores the input saturation and the parameter uncertainty caused by the linearization error, it takes a long time to complete the spacecraft orbit rendezvous task, and further proposes a method that considers linearization Gain-scheduled control method for error-based space rendezvous systems

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Space rendezvous system gain scheduling control method with linearization errors taken into consideration
  • Space rendezvous system gain scheduling control method with linearization errors taken into consideration
  • Space rendezvous system gain scheduling control method with linearization errors taken into consideration

Examples

Experimental program
Comparison scheme
Effect test

specific Embodiment approach 1

[0067] Specific embodiment one: the gain scheduling control method of the space rendezvous system considering the linearization error, it comprises the following steps:

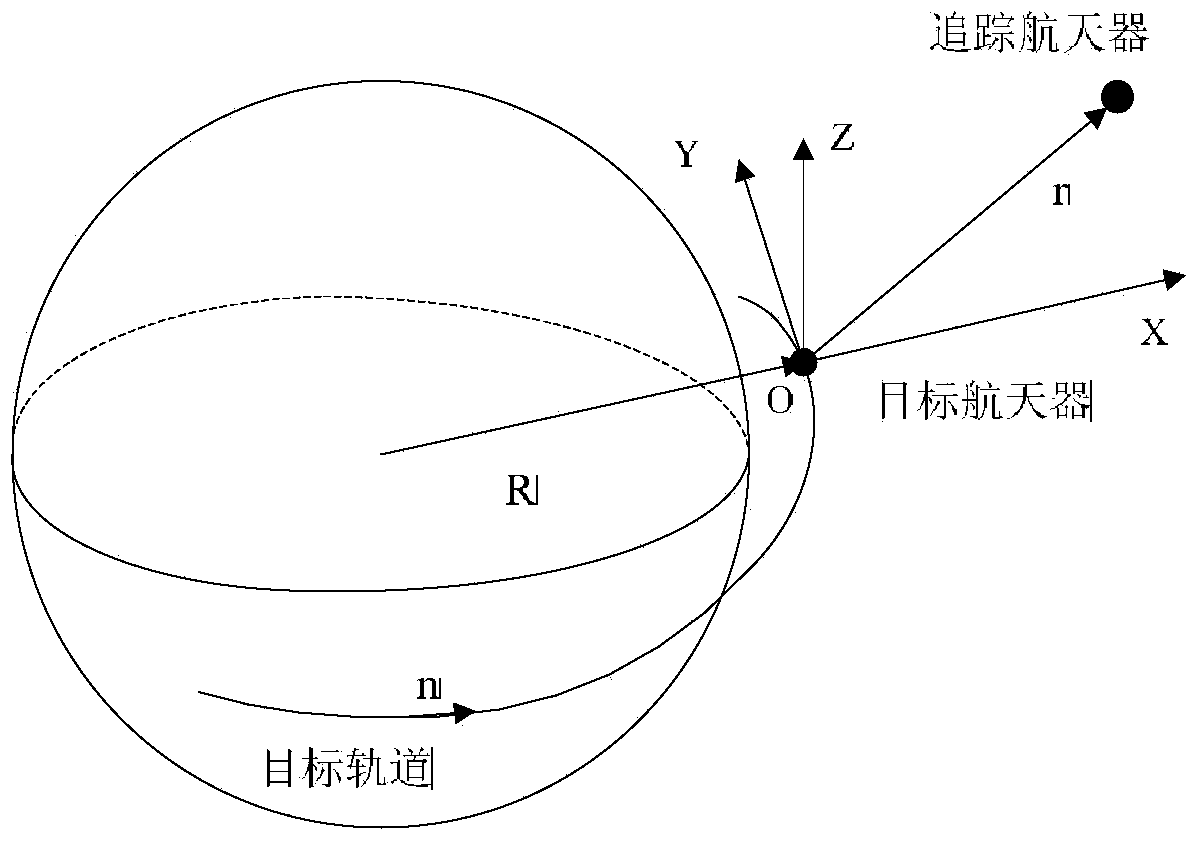
[0068] Step 1: When the two spacecraft are performing the rendezvous mission, one spacecraft passively flies in orbit, which is called the target spacecraft; the other spacecraft maneuvers under the action of the control force, and flies to the target spacecraft with different rules. It is called tracking spacecraft; assume that the target spacecraft is running on a circular orbit with a radius of R; for the convenience of description, the orbital coordinate system O-XYZ of the target spacecraft is introduced, its origin O is located at the center of mass of the target spacecraft, and the X axis is along the circular orbit The direction of the radius R, the Y axis is along the direction of tracking the flight of the spacecraft, and the Z axis points out of the orbital plane to form a right-handed coordinate sy...

specific Embodiment approach 2

[0124] Specific embodiment 2: γ corresponding to "the initial relative motion state vector is X(0)" in step 3 described in this embodiment 0 The solution process is:

[0125] For the initial relative motion state vector X(0), γ 0 is the only solution to the nonlinear equation (17):

[0126] ρ ( γ 0 ) X 0 T P ( γ 0 ) X 0 = 1 - - - ( 17 )

[0127] Since P(γ) is monotonic with respect to γ, the nonlinear equation (17) can be solved by dichotomy.

[0128] Other steps are the same as in the first embodiment.

specific Embodiment approach 3

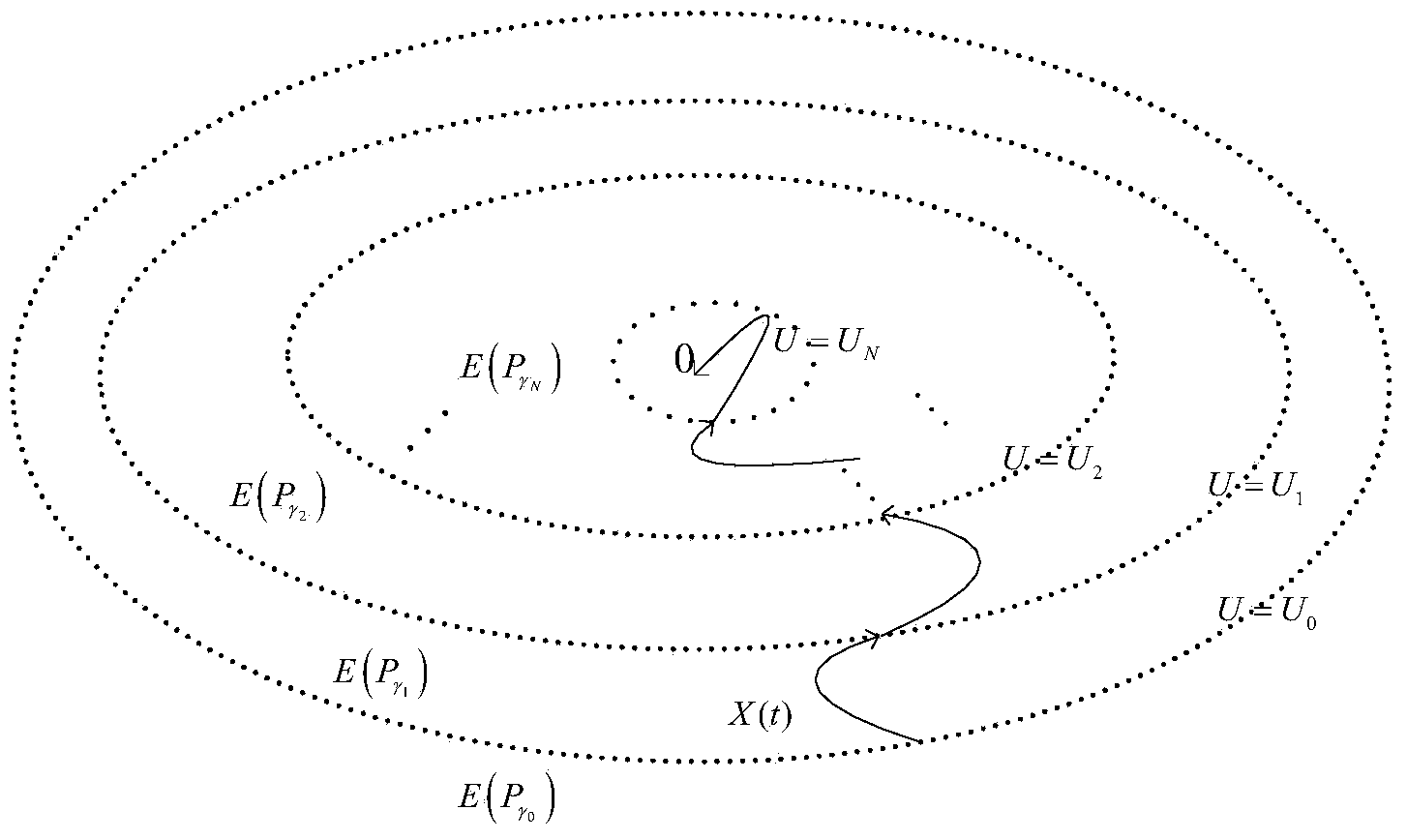
[0129] Specific embodiment three: in the step 3 described in this embodiment mode " gain scheduling controller (15) begins to work in spacecraft orbit rendezvous system, controller (15) according to U 0 → U 1 →…→U N-1 → U N The order of is applied to formula (6)" and the realization process is as follows:

[0130] Set a current variable r, its initial value is r=0 and the corresponding controller is U=U 0 , if r≤N-1, for the relative motion state vector X(t) at each moment, calculate

[0131]

[0132] if Then the gain scheduling controller U=U r+1 And let r=r+1; otherwise gain-scheduled controller U=U r , the relative motion state vector X enters the inner ellipsoid sequentially from the outermost ellipsoid; when the gain scheduling controller switches to U=U N When , the relative motion state vector X enters the innermost ellipsoid, and finally converges to the equilibrium point, and the controller does not switch anymore, that is, there is no need to calculate for...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention provides a space rendezvous system gain scheduling control method with linearization errors taken into consideration, and relates to a spacecraft orbit rendezvous gain scheduling control method. The space rendezvous system gain scheduling control method solves the problem that due to the fact that according to an existing aircraft orbit rendezvous control method, input saturation and parameter uncertainty caused by the linearization errors are ignored, time consumption is high when an aircraft orbit rendezvous task is completed. According to the space rendezvous system gain scheduling control method, the parameter uncertainty caused by the linearization errors is taken into consideration and endowed with exact meanings, an aircraft orbit rendezvous relative movement model is established, a gain scheduling controller of an aircraft orbit rendezvous is then designed, the aircraft orbit rendezvous is controlled through the gain scheduling controller, and the rendezvous task is completed. The space rendezvous system gain scheduling control method is mainly used for controlling the aircraft orbit rendezvous.

Description

technical field [0001] The invention relates to a gain scheduling control method of a spacecraft orbit rendezvous system. Background technique [0002] Spacecraft orbital rendezvous is a very important flight operation technique. A successful rendezvous is a prerequisite for some advanced space operations, such as on-orbit assembly, recovery, resupply and maintenance of large infrastructure such as space stations, space laboratories, space communication and remote sensing platforms, and international space rescue services. The orbit control problem of spacecraft rendezvous is one of the important components of spacecraft rendezvous and docking technology. In the past few decades, the problem of orbital rendezvous control of spacecraft has received extensive attention. [0003] Orbital rendezvous is subject to general constraints, of which the constraints on the acceleration that the thrusters can produce are critical. This is because if the acceleration obtained according...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): G05D1/10G05B13/04
Inventor 周彬王茜段广仁
Owner 哈尔滨工业大学人工智能研究院有限公司
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com