Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Finite time convergence time-varying sliding mode attitude control method

An attitude control, limited time technology, applied in attitude control and other directions, can solve problems such as jumping and poor robustness, and achieve the effect of eliminating jumping problems and enhancing robustness.

Inactive Publication Date: 2016-01-13
BEIJING INSTITUTE OF TECHNOLOGYGY
View PDF6 Cites 41 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0006] Poor robustness, high-frequency chattering, and jumping problems that may be caused by adding time-varying items in the existing technology

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Finite time convergence time-varying sliding mode attitude control method
  • Finite time convergence time-varying sliding mode attitude control method
  • Finite time convergence time-varying sliding mode attitude control method

Examples

Experimental program
Comparison scheme
Effect test

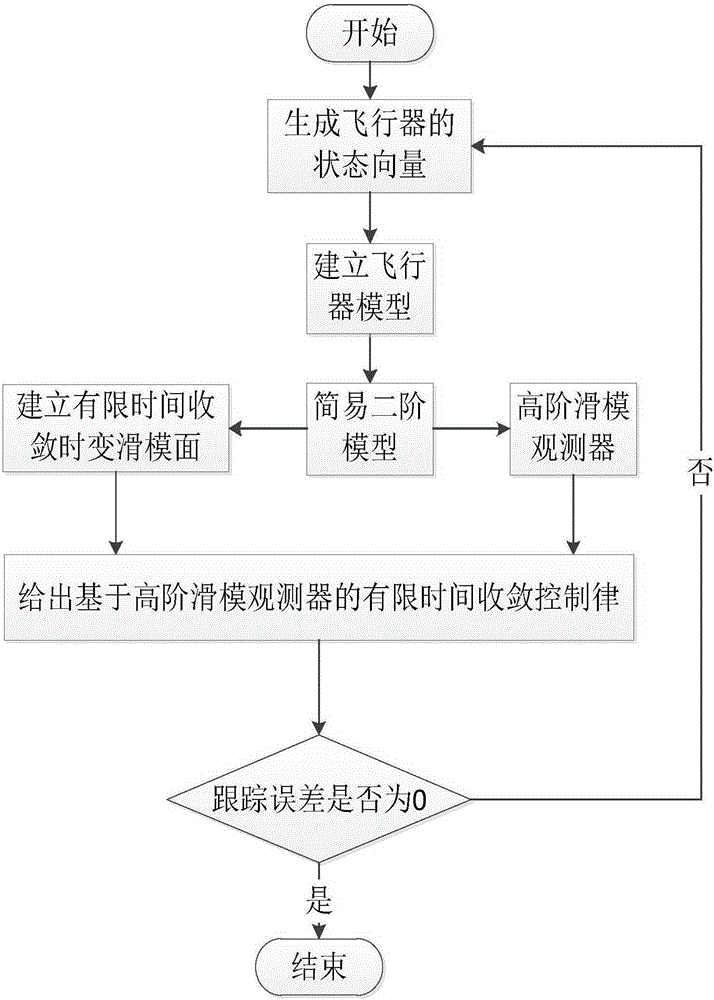
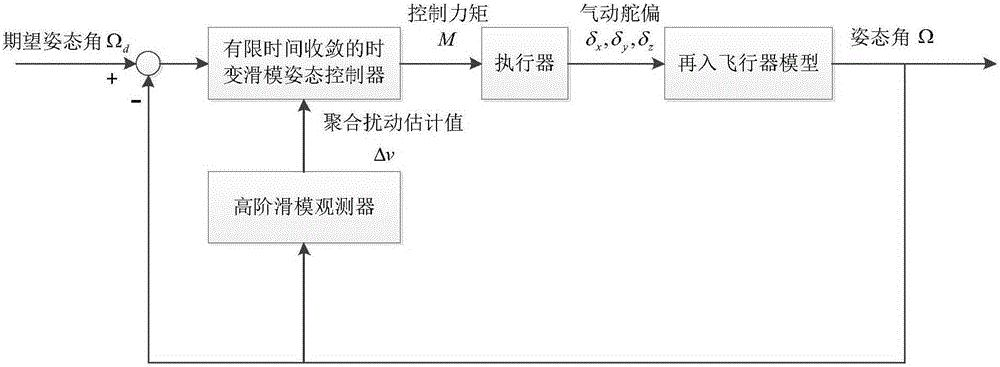
Embodiment 1

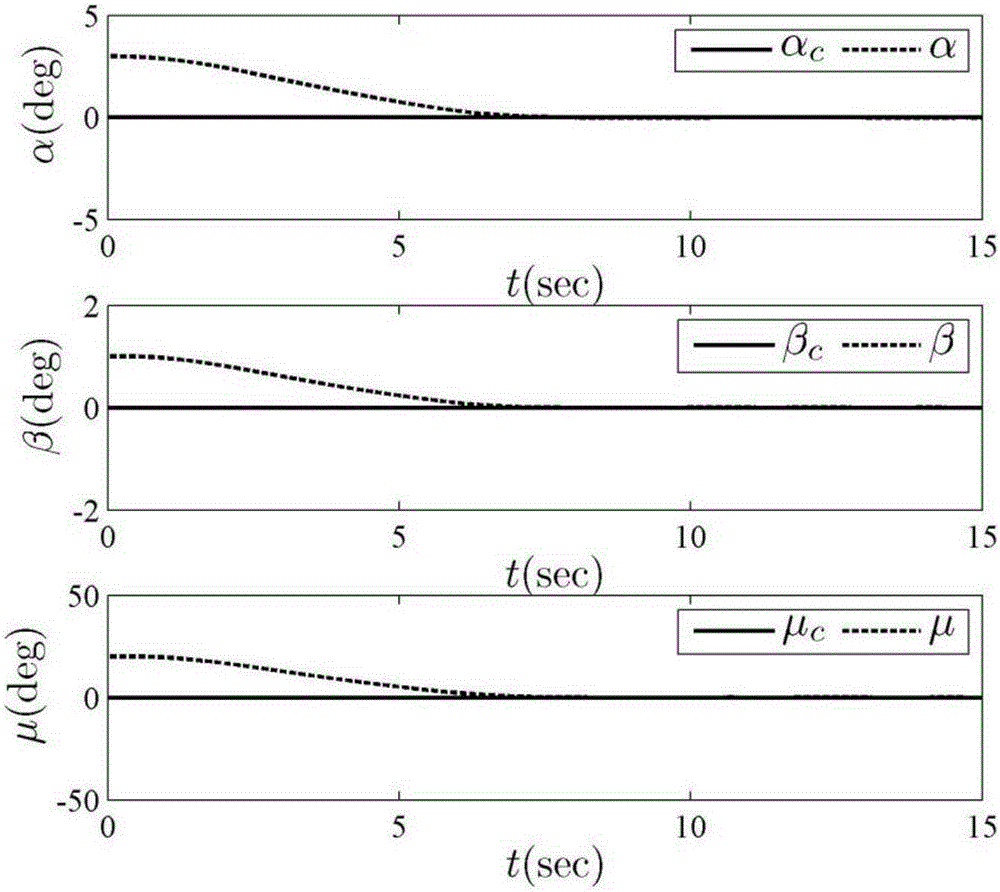
[0100] Using the hypersonic model of the Winged-Cone configuration announced by NASA as the simulation platform, the numerical simulation is carried out for its re-entry flight process. In the simulation, the initial altitude is 28km, the speed is 2800m / s, the initial attitude angle is [3120]deg, and the desired attitude angle is [000]deg. The initial attitude angular velocity is 0.

[0101] Since the flight conditions of the re-entry vehicle vary widely, and often have uncertainties such as aerodynamic parameter perturbation, for the problem of attitude control of the re-entry vehicle, it is necessary not only to test the control performance under nominal conditions, but also to test the control performance of the controller in In the case of drastic changes in environmental parameters and strong uncertainties in the system, whether robust and precise control can be performed. In order to further verify the robustness of the system, add a large external disturbance (directly...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The present invention discloses a finite time convergence time-varying sliding mode attitude control method, relating to a finite time convergence time-varying sliding mode reentry aircraft attitude control method based on a high order sliding mode observer, belonging to the technical field of aircraft attitude control. The invention discloses the finite time convergence time-varying sliding mode attitude control method, on the basis of aircraft attitude model feedback linearization, high-frequency vibration is weakened based on a low-pass filter, the arrival segment of slip mode control can be eliminated through introducing a time-varying item, the robustness of a system is enhanced, a jump problem caused by time-varying function first-order derivative discontinuity can be eliminated, and the time-varying sliding mode attitude control of finite time convergence is realized. According to the method, the reentry aircraft attitude control tracking error can be converged to zero in a finite time, the jump phenomenon caused by the first-order derivative discontinuity of a time-varying item can be eliminated, the high frequency vibration is weakened, and the robustness of a reentry aircraft attitude control system can be improved.

Description

technical field [0001] The invention relates to an attitude control method of a time-varying sliding mode reentry aircraft with finite time convergence, in particular to a time-varying sliding mode reentry aircraft attitude control method based on a finite time convergence of a high-order sliding mode observer, which belongs to aircraft attitude control technology field. Background technique [0002] The attitude control design problem of re-entry aircraft becomes extremely complicated due to the large range of flight conditions during re-entry flight, serious coupling between channels, strong nonlinear dynamic characteristics, various uncertain external disturbances and uncertain parameters. . The key to the design of re-entry vehicle control system is to solve the influence of the above-mentioned strong nonlinearity, strong coupling, fast time-varying and uncertainty on the system performance. [0003] Sliding mode control has the characteristics of global convergence, e...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): G05D1/08
Inventor 盛永智薛晨琛刘向东
Owner BEIJING INSTITUTE OF TECHNOLOGYGY
Features
  • Generate Ideas
  • Intellectual Property
  • Life Sciences
  • Materials
  • Tech Scout
Why Patsnap Eureka
  • Unparalleled Data Quality
  • Higher Quality Content
  • 60% Fewer Hallucinations
Social media
Patsnap Eureka Blog
Learn More

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com