Method for tracking and controlling locus of unmanned bicycle

A trajectory tracking and control method technology, which is applied in vehicle position/route/height control, non-electric variable control, position/direction control, etc., can solve the influence of bicycle trajectory, cannot obtain the best effect, cannot obtain tracking effect, etc. problem, the effect of achieving good results

Active Publication Date: 2016-02-10
TSINGHUA UNIV
View PDF5 Cites 38 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

However, for a bicycle, the balance dynamic model of the bicycle will cause a more complicated dynamic process when the handlebar of the bicycle turns to the target corner, which will have a greater impact on the trajectory of the bicycle.
Therefore, in the problem of bicycle trajectory tracking, it is u

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Method for tracking and controlling locus of unmanned bicycle
  • Method for tracking and controlling locus of unmanned bicycle
  • Method for tracking and controlling locus of unmanned bicycle

Examples

Experimental program
Comparison scheme
Effect test

Example Embodiment

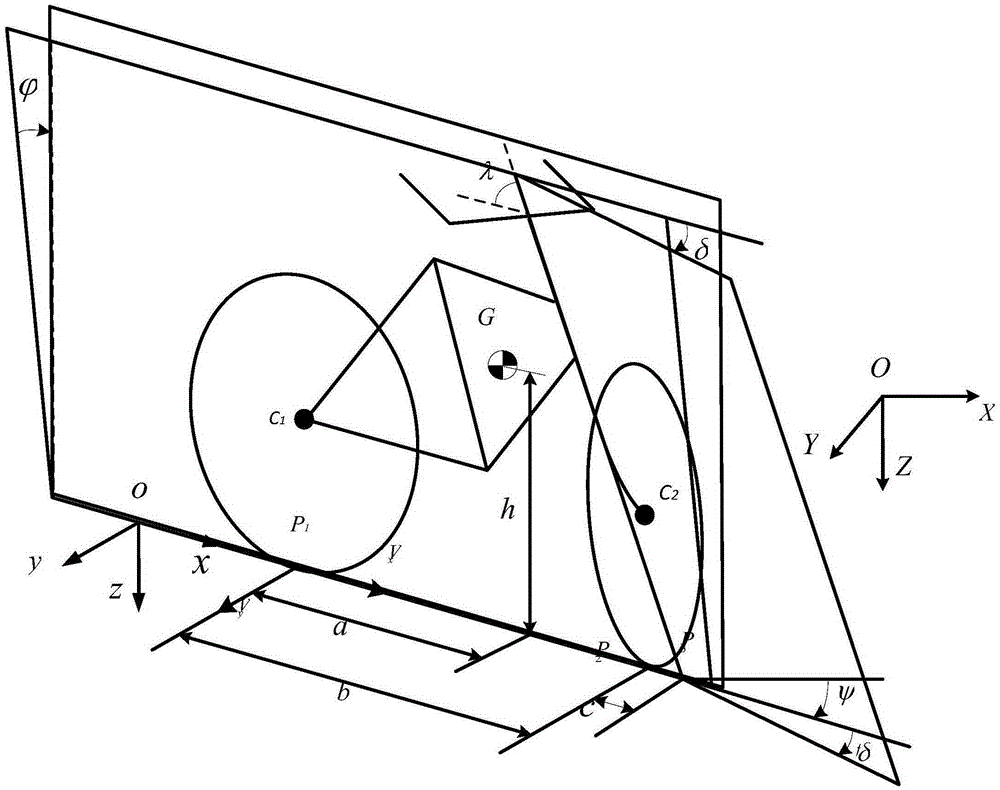
[0069] The following describes in detail the trajectory tracking control method of an unmanned bicycle proposed by the present invention with reference to the accompanying drawings.

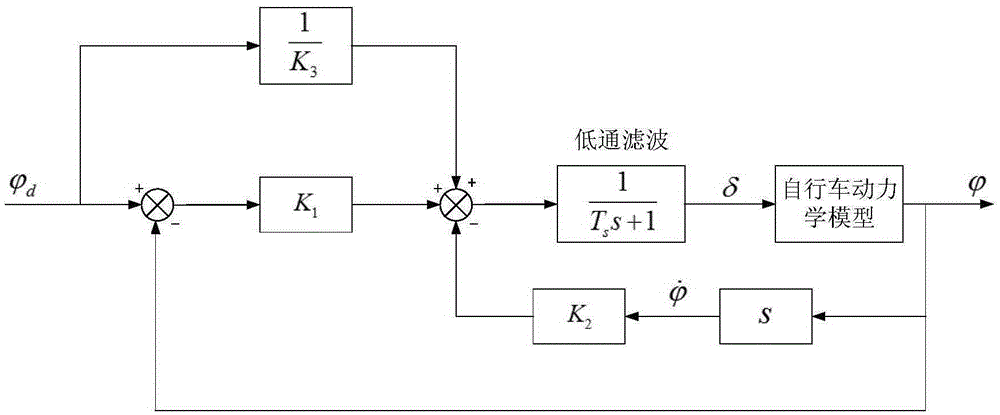
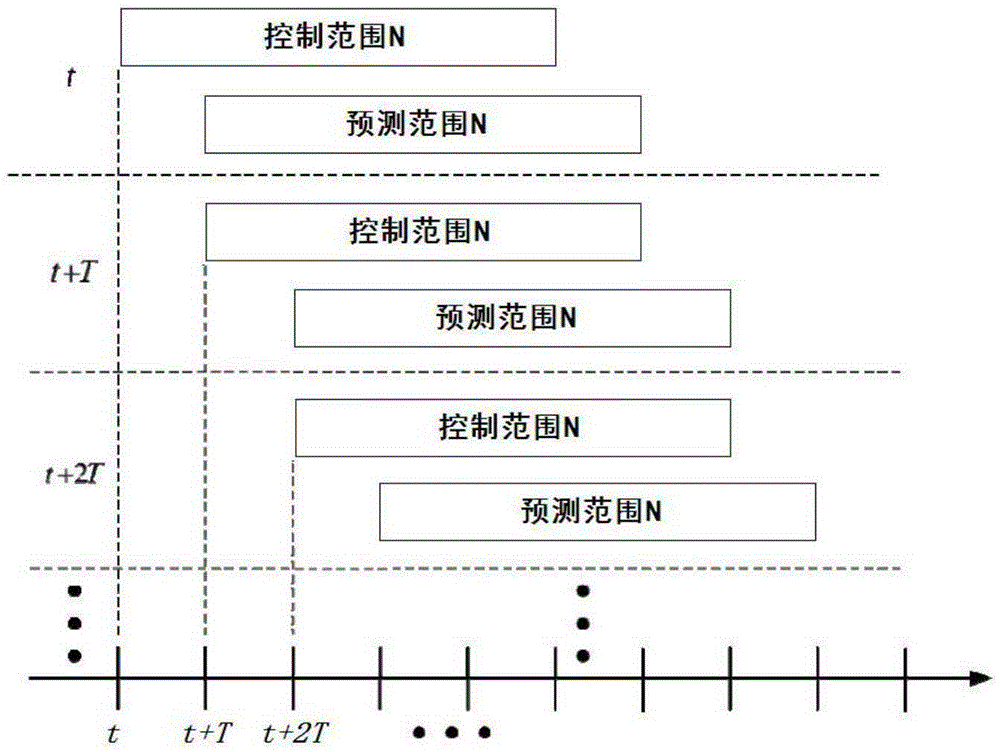
[0070] The invention uses the model predictive control algorithm to carry out the trajectory tracking control of the bicycle. First, for the bicycle, establish its balance dynamics model, and establish the system state equation after adding the self-balance controller; secondly, establish the bicycle kinematics model and linearize it; then compare the kinematics model with the self-balance control system Combined, after corresponding simplification processing, a seven-dimensional state prediction model is established; finally, the linear quadratic index function is selected, the weight matrix parameters are set, and the optimal control input at each sampling time is solved online. Picture 8 It is a flowchart of the trajectory tracking control method of the unmanned bicycle of the present invention. ...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to view more

PUM

No PUM Login to view more

Abstract

The invention belongs to the technical field of movement controlling of unmanned vehicles, and especially relates to a method for tracking and controlling a locus of an unmanned bicycle. The method comprises the steps of: firstly, establishing a balance dynamic model of the bicycle, and establishing discrete state equations of a bicycle self-balance control system into which a self-balance controller is added; secondly, establishing a discrete kinetic model of the bicycle, and carrying out linearization; then combining the kinetic model with the self-balance control system, carrying out corresponding simplification processing, and establishing a seven-dimension state predicting model of the bicycle; and finally, using the seven-dimension state predicting model as a prediction model of a bicycle locus tracking algorithm, carrying out locus tracking and controlling on the bicycle, and solving optimal control input of each sampling moment on line. The bicycle locus tracking and controlling method based on the seven-dimension state predicting model is capable of accurately predicting the state of the bicycle in the future time, the calculation amount is small, and a good control effect is ensured by the on-line real-time performance.

Description

technical field [0001] The invention belongs to the technical field of motion control of unmanned bicycles, and in particular relates to a method for track tracking control of unmanned bicycles. Background technique [0002] Compared with cars, unmanned bicycles have the advantages of low price, light and portable, flexible mobility, environmental protection and energy saving. However, compared to the four-wheel structure of a car, the two-wheel structure of a bicycle is unstable, and the bicycle cannot maintain balance without human control. Therefore, for a bicycle, in order to realize the function of unmanned driving, it must first be able to control its own balance. It can be seen that the realization of unmanned bicycles is much more difficult than that of unmanned cars. [0003] On the basis of realizing the self-balancing control of the bicycle, it is necessary to carry out motion control on it, cooperate with the functions of upper-level machine vision and trajecto...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to view more

Application Information

Patent Timeline
no application Login to view more
IPC IPC(8): G05D1/00
Inventor 赵明国余永超
Owner TSINGHUA UNIV
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Try Eureka
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap