Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Attitude control thruster layout optimization method for combined spacecraft

A thruster layout and combined spacecraft technology, which is applied in the field of satellite attitude control, can solve the problems of thruster layout optimization, etc., and achieve the effect of prolonging the working life of the orbit and reducing fuel consumption

Active Publication Date: 2016-08-10
BEIJING INSTITUTE OF TECHNOLOGYGY +1
View PDF7 Cites 31 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

However, these two methods are all researches on a single spacecraft, and there is little research on the thruster layout optimization problem of a combined spacecraft consisting of a life extension vehicle and a target satellite.

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Attitude control thruster layout optimization method for combined spacecraft
  • Attitude control thruster layout optimization method for combined spacecraft
  • Attitude control thruster layout optimization method for combined spacecraft

Examples

Experimental program
Comparison scheme
Effect test

Embodiment Construction

[0149] The present invention will be further described below in conjunction with the accompanying drawings and embodiments.

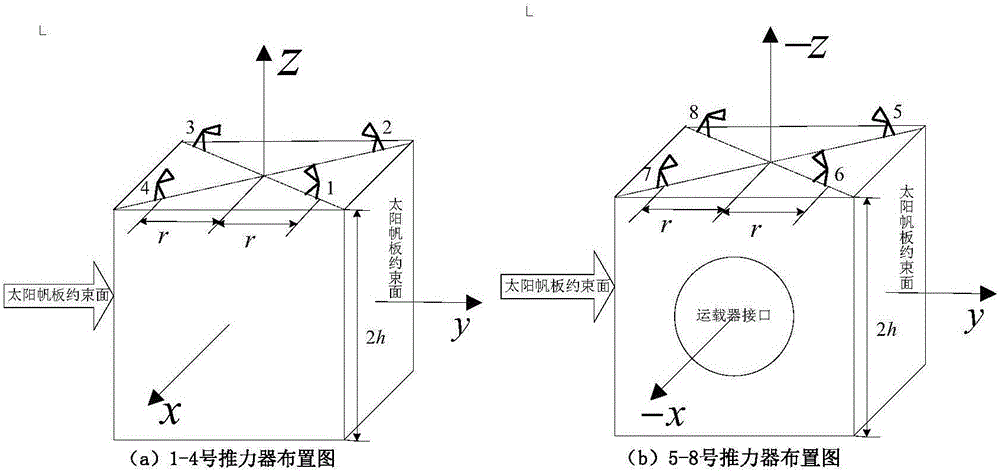
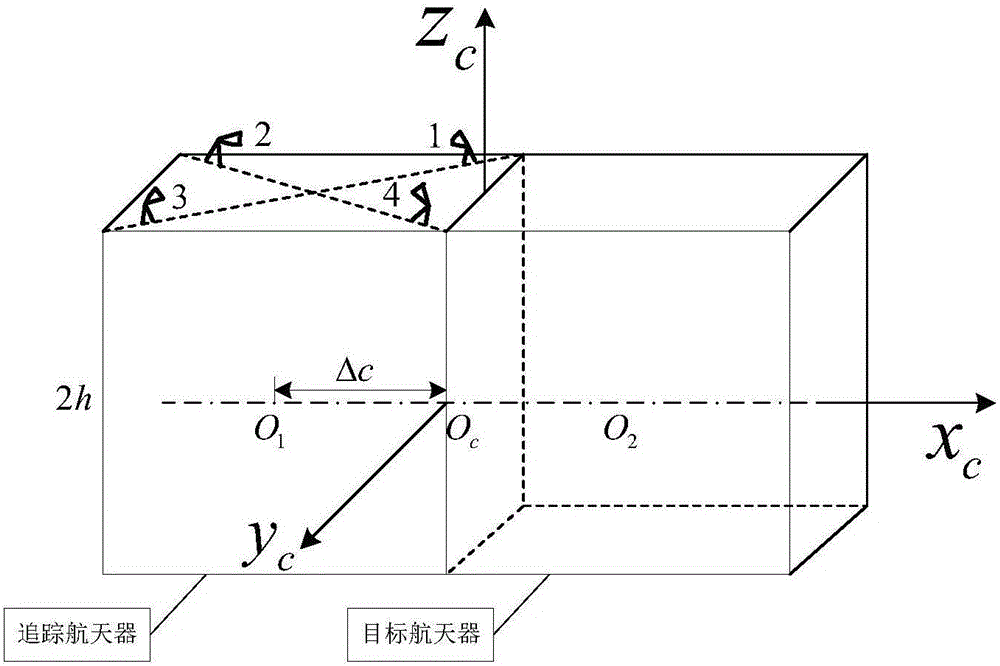
[0150] A method for optimizing the layout of a combined spacecraft attitude control thruster according to the present invention takes a tracking spacecraft in the shape of a cube (2m×2m×2m) as the research object, which has the same shape as the target satellite it docks with. The tracking spacecraft is configured as figure 1 , figure 2 As shown, the configuration of the combined spacecraft after rendezvous and docking is as follows image 3 shown.

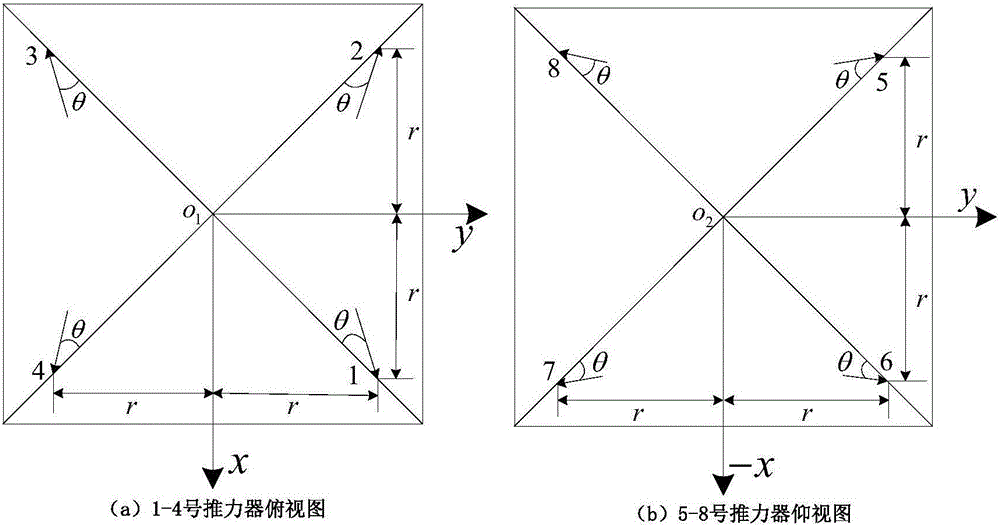
[0151] The rotation mode of the universal joint installed at the joint of the thruster is as follows: Figure 4 , Figure 5 shown. The universal joints are installed on the thrusters 1, 2, 1 and 2 of the combined spacecraft respectively, and the simulation is carried out according to the different rotation modes of the universal joints.

[0152] Its simulation parameters are as follows:

[0153] Tab...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention relates to an attitude control thruster layout optimization method for a combined spacecraft and belongs to the technical field of satellite attitude control. According to the method, firstly, a thruster is obliquely mounted; secondly, a universal joint with two freedoms is additionally mounted at a joint portion of the thruster; thirdly, a thruster thrust distribution model is designed under constraints of minimum fuel consumption and a universal joint rotation angle according to a desired control torque; lastly, according to an attitude angle and attitude angle speed change fed back by a sensor, the opening / closing and blowing duration of the thruster is controlled through a phase plane control method. Rapid attitude maneuvering of the spacecraft is realized, fuel consumption is reduced, and a complete control circuit is formed. Through the method, a blowing direction of the thruster is driven to change on the basis of rotation of the universal joint, a problem of unstable control caused by large-scale mass center offset because of rendezvous and docking is effectively solved; fuel consumption can be reduced, and on-orbit service life of the thruster is prolonged.

Description

technical field [0001] The invention relates to a layout optimization method for attitude control thrusters of combined spacecraft, in particular to a layout optimization method for attitude control thrusters of an assembly composed of rendezvous and docking spacecraft, which belongs to the technical field of satellite attitude control. Background technique [0002] Long life and high reliability are the main performance requirements and important features of my country's development of a new generation of large-scale geostationary satellite platforms. However, due to the constraints of the satellite platform's fuel carrying capacity, even if the on-board payload and other components are still in the working life, the fuel Depletion causes the satellite's propulsion system to fail and leads to the failure of the satellite as a whole. By launching a life-extending spacecraft, completing the docking with the geostationary orbit satellite at the end of its life, using methods su...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): G05D1/08G05B13/04
CPCG05B13/042G05D1/0808
Inventor 张景瑞徐凯周志成李新刚张尧
Owner BEIJING INSTITUTE OF TECHNOLOGYGY
Features
  • Generate Ideas
  • Intellectual Property
  • Life Sciences
  • Materials
  • Tech Scout
Why Patsnap Eureka
  • Unparalleled Data Quality
  • Higher Quality Content
  • 60% Fewer Hallucinations
Social media
Patsnap Eureka Blog
Learn More

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com