Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Coefficient mapping transformation-based polynomial complete homomorphic encryption method and system

A technology of homomorphic encryption and mapping transformation, applied in the field of information security, can solve the problems of no commercial application instance of homomorphic encryption algorithm, large computing and storage resources, and inability to effectively control noise, etc. The effect of speed increase, ciphertext size and expansion speed is small

Active Publication Date: 2016-11-23
郑珂威
View PDF4 Cites 27 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

Coron, Lepoin, Tibouchi's Batch Fully Homomorphic Encryption over the Integers (EUROCRYPT 2013Springer) has been improved on the basis of the original method, so that the encryption for all bits can be compressed into the same ciphertext, which effectively reduces the size of the ciphertext. It also reduces the amount of calculation to a certain extent, but it cannot effectively control the noise, so data cleaning operations are still required
[0006] The research results listed above, as well as almost all other researches, cannot completely deviate from the idea and framework of Craig’s original method. Therefore, although the new method has made great improvements compared with the original method, the actual implementation of the algorithm requires the consumption of computing resources and Storage resources are still huge, and it is difficult to actually apply them to actual services
This is also the reason why there are no commercial application examples of homomorphic encryption algorithms in the world so far despite the obvious demand

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Coefficient mapping transformation-based polynomial complete homomorphic encryption method and system
  • Coefficient mapping transformation-based polynomial complete homomorphic encryption method and system
  • Coefficient mapping transformation-based polynomial complete homomorphic encryption method and system

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

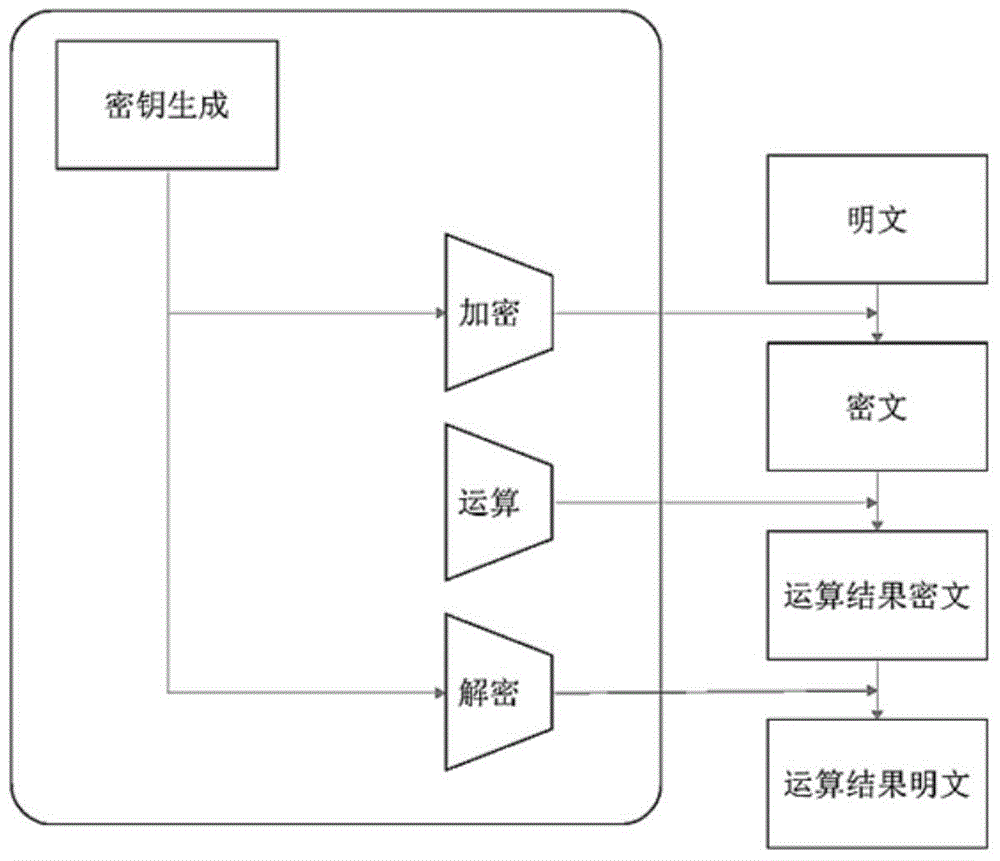
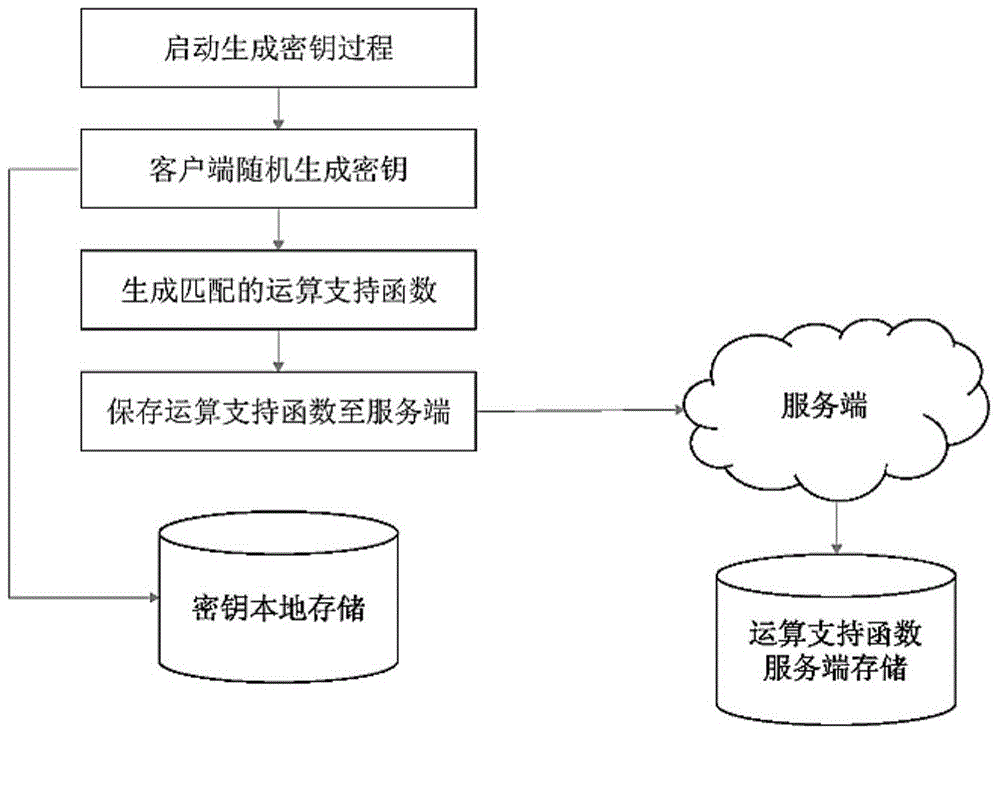
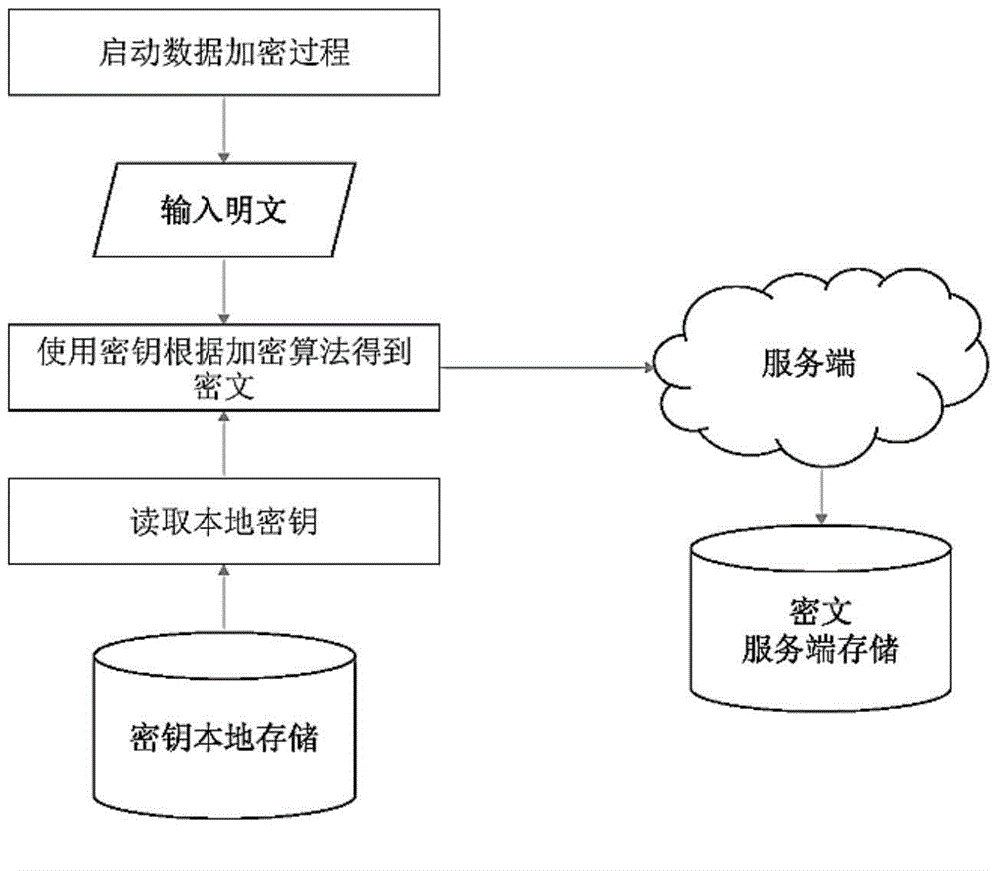
[0036] The present invention can be implemented in various ways corresponding to different demand environments and application scenarios, including: USBKey implementation, API implementation, SDK implementation, chip implementation, expansion card implementation, special equipment implementation, etc. Such as figure 1 and figure 2 As shown, any implementation method includes: client and server. The steps of a typical homomorphic encryption operation process are as follows:

[0037] 1) The client invokes the locally stored key to encrypt sensitive plaintext data and obtain the ciphertext;

[0038] 2) The client sends the ciphertext and calculation requirements to the server, and the key is kept on the client;

[0039] 3) The server calls the corresponding operation support function family, and uses the homomorphic operation function to perform the required operation on the ciphertext uploaded by the client, and then returns the ciphertext of the operation result;

[0040] 4...

Embodiment 2

[0111] The difference between this embodiment and Embodiment 1 lies in that the operation support function G used in it includes:

[0112] Where: α, β∈X, h 1 (α,β), h 2 (α,β) and h 3 (α,β) to satisfy h1 (α,β)≠h 2 (α,β)≠h 3 Any function of (α,β)≠α≠β;

[0113] The corresponding homomorphic operations specifically include:

[0114] i) Addition and subtraction of ciphertext and ciphertext: C r =C 2 ±C 1 , C r ={A r ,X r ,B r},in:

[0115] A r = { a ri | i ∈ I } , a ri = a 2 i · g 1 ( x 2 i , x 1 i ...

Embodiment 3

[0131] In order to improve security, this embodiment introduces the function f when generating the operation support function G 2 , this function does not need to be added to the key, and only affects the calculation and expression of the operation support function G, which can be understood as encrypting the operation support function G.

[0132] The specific expression is as follows: Where: α, β∈X, h 1 (α,β), h 2 (α,β), h 3 (α,β) and h 4 (α,β) to satisfy h 1 (α,β)≠h 2 (α,β)≠h 3 (α,β)≠h 4 Any function of (α,β)≠α≠β; f 2 () is a random generation function used to encrypt the operation support function,

[0133] The corresponding homomorphic operations specifically include:

[0134] i) Addition and subtraction of ciphertext and ciphertext: C r =C 2 ±C 1 , C r ={A r ,X r ,B r}, where: A r ={a ri |i∈I},

[0135] a ri =g 6 ·[a 2i g 1 (x 2i ,x 1i ) g 3 (h 1 (x 2i ,x 1i ), h 2 (x 2i ,x 1i ))±a 1i g 2 (x 2i ,x 1i ) g 4 (h 1 (x 2i ,x 1i ), h 2...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention relates to a coefficient mapping transformation-based polynomial complete homomorphic encryption method and a system. According to the method, a plaintext is expressed as a polynomial of a specified mapping function, wherein the polynomial is composed of a set of random values, two sets of random coefficient factors and a random constant, and the expression of the specified mapping function and one set of random coefficient factors are adopted as a key; the other set of random coefficient factors, one set of random independent variables of the mapping function, and the random constant are adopted as a ciphertext which can be subjected to homomorphic operation; three kinds of different mapping is carried out on the key part of the function, and numerical value fitting is carried out, so that an operation support function family composed of three sub-functions is obtained; and after operation support function family-based ciphertext homomorphic operation is carried out at a different place, the method returns to a local place, and encryption is carried out through the key. With the coefficient mapping transformation-based polynomial complete homomorphic encryption method and the system of the invention adopted, true value of data is only visible to a data owner possessing the key, and the data present as a ciphertext at a data storage side, a data transmission pipeline and a data operation side which cannot guarantee the security of the data, and therefore, a secure data storage and operation environment can be ensured.

Description

technical field [0001] The present invention relates to a technology in the field of information security, in particular to a polynomial complete homomorphic encryption method and system based on coefficient mapping transformation. Background technique [0002] Homomorphic encryption is an encryption method that processes homomorphically encrypted data to obtain an output, and decrypts this output, and the result is the same as the output obtained by processing the unencrypted original data in the same way . [0003] In 1978, Rivest, Adleman and Dertouzos first proposed the concept of homomorphic encryption in On Data Banks and Privacy Homomorphisms. (Foundations of Secure Communication, pp.169‐177, Academic Press.), when they used the term privacy homomorphism (privacy homomorphism). In this paper, Rivest et al. proposed several candidate encryption algorithms at the same time, which have the characteristics of homomorphic operation. Polynomial encryption algorithm is on...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): H04L9/00
CPCH04L2209/46H04L9/3093G09C1/00H04L9/008H04L9/0861
Inventor 郑珂威
Owner 郑珂威
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com