Local projection and global interpolation-based nonlinear model reduction method
A local projection and interpolation technology, applied in special data processing applications, instruments, electrical digital data processing, etc., can solve the problems that the scale of the reduced-order system cannot be significantly reduced, and the scale of the global projection matrix is large.
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
Image
Examples
Embodiment 1
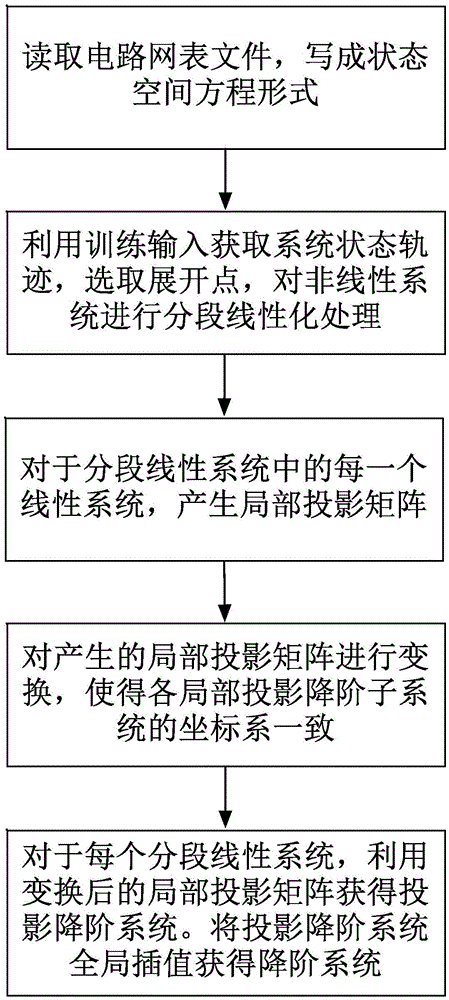
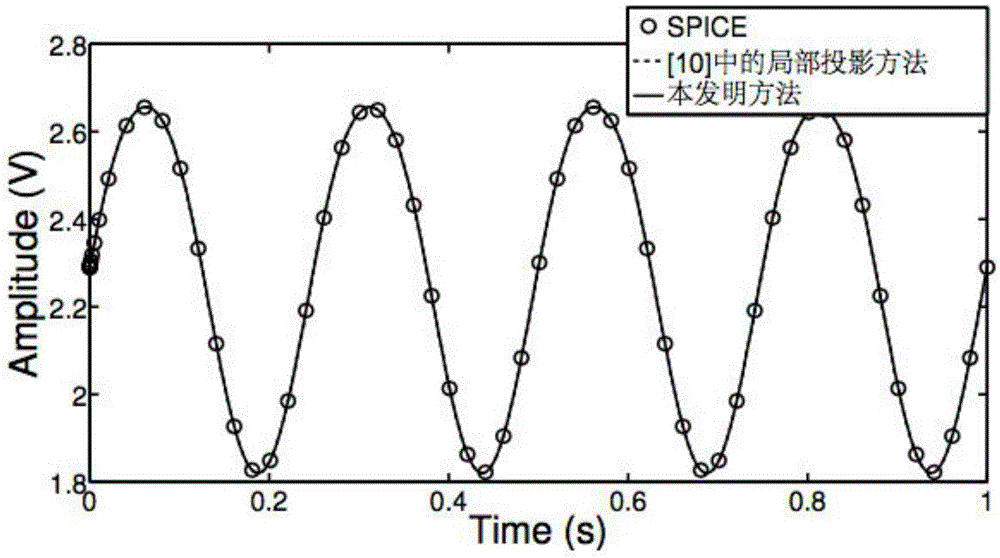
[0048] A second-order telescopic amplifier, the circuit contains 28 MOS tubes, and the original order of the circuit is 83; through a series of training inputs, 72 expansion points are obtained, and v=1.5+0.01sin (8pt) is used as the test input Test the reduced-order accuracy; the time required for SPICE to simulate the original circuit is 0.068 seconds.
[0049] In this embodiment, 72 expansion points are divided into 15 groups, and each group constructs a projection matrix of order 9. For each group of expansion points, the projection matrices of order 9 are aggregated together and a local projection of order 15 is obtained by SVD Then, use coordinate transformation to transform these 15-order local projection matrices into unified coordinates, and then perform global interpolation. The time required for system simulation after global interpolation is 0.0124s; the number of local reduced-order systems that this method needs to store is 15;
[0050] As a comparison, in this ...
Embodiment 2
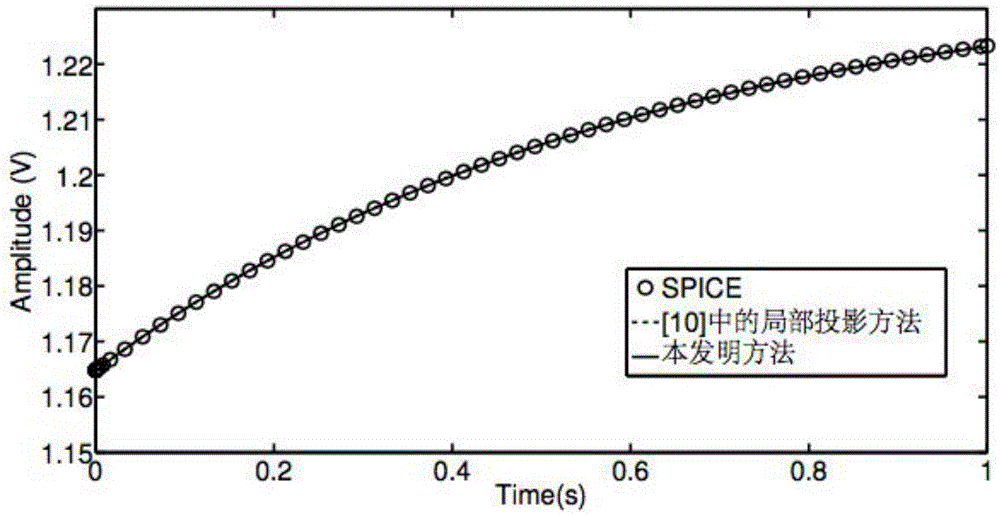
[0053] A current mirror amplifier, the original order of the circuit is 70, through a series of training inputs, 66 expansion points are obtained, using As a test input to test the reduced-order accuracy, the time required for SPICE to simulate the original circuit is 2.25 seconds.
[0054] In this embodiment, 66 expansion points are divided into 13 groups, and each group constructs a 13th-order local projection matrix, and then uses coordinate transformation to transform these 13th-order local projection matrices into uniform coordinates, and then performs global interpolation. The time required for system simulation after interpolation is 0.0218s, and the number of local reduced-order systems required to be stored by this method is 13.
[0055] As a comparison, the 66 expansion points are divided into 60 overlapping groups by using the method of literature [10]. The order of each local reduction system in these overlapping groups is 13, and the order of the global system is...
Embodiment 3
[0058] A clock drive circuit, the original order of the circuit is 5642; through a series of training inputs, 439 expansion points are obtained, and a pulse signal different from the training input is used as the test input to test the order reduction accuracy, which is required for SPICE simulation of the original circuit The time is 290.86 seconds.
[0059] In this embodiment, 439 expansion points are divided into 55 groups, and each group constructs a 180-order local projection matrix, and then uses coordinate transformation to transform these 180-order local projection matrices into uniform coordinates, and then performs global interpolation. The time required for system simulation after interpolation is 0.318s; the number of local reduced-order systems required to be stored by the method of the present invention is 55, and the required storage capacity is 219MB;
[0060] As a comparison, in this embodiment, the method of literature [10] is used to divide 439 expansion poi...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com