Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Method for recognizing chaotic time series based on random matrix theory

A technology of chaotic time series and random matrix theory, applied in the field of identification of chaotic time series, can solve the problems of long time series length, susceptibility to noise interference, inability to identify chaotic time series, etc., and achieve simple processing process and universal applicability and the effect of robustness

Pending Publication Date: 2017-11-24
CHINA UNIV OF MINING & TECH
View PDF2 Cites 1 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

Since the algorithm for calculating the above characteristic values ​​requires a long time series and is susceptible to noise interference, the application of these methods will be limited in some short or noisy chaotic time series, so that it cannot be accurately calculated. Identify chaotic time series

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Method for recognizing chaotic time series based on random matrix theory
  • Method for recognizing chaotic time series based on random matrix theory
  • Method for recognizing chaotic time series based on random matrix theory

Examples

Experimental program
Comparison scheme
Effect test

Embodiment Construction

[0057] The present invention will be further described below.

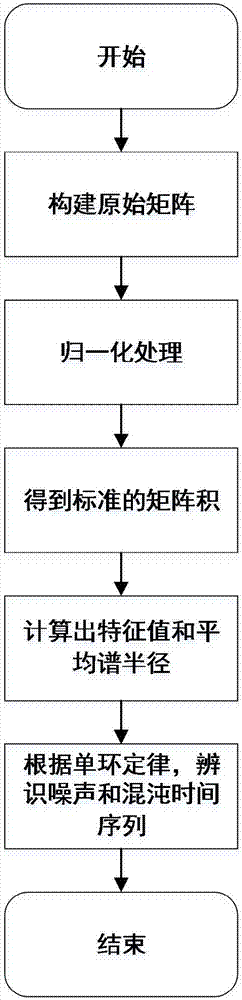
[0058] Such as figure 1 Shown, concrete steps of the present invention are:

[0059] A. Randomly select the pre-identified time series, the selection range of which is one of the noise time series and the time series of the known chaotic system, and construct the original matrix X according to the time series; when the amount of acquired data is sufficient When, these data are regarded as a time series V=(v 1 ,...v i ,...v i+MN ,...v T ), you can use some or all elements of V to construct an M×N original matrix X;

[0060]

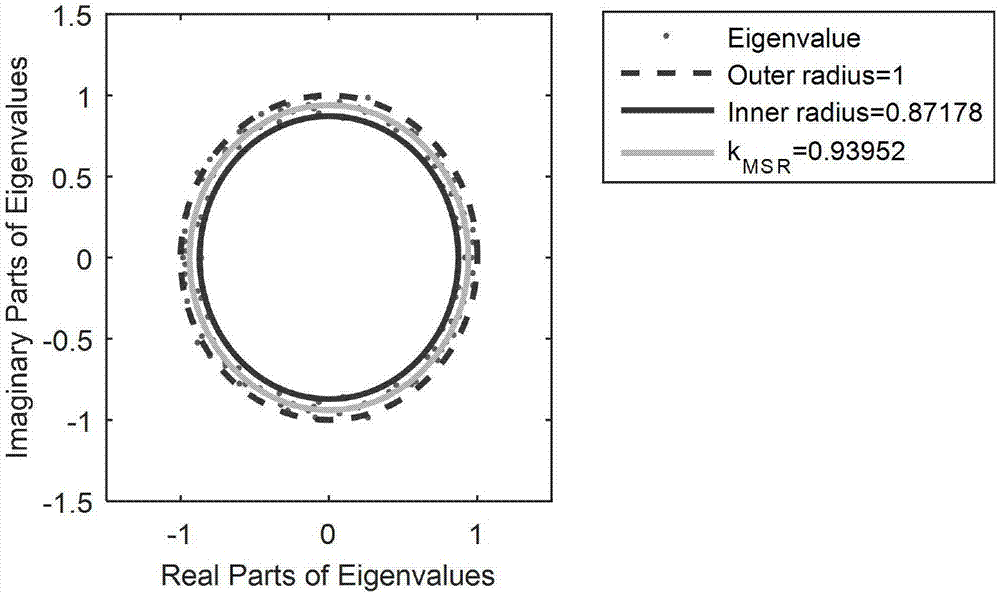
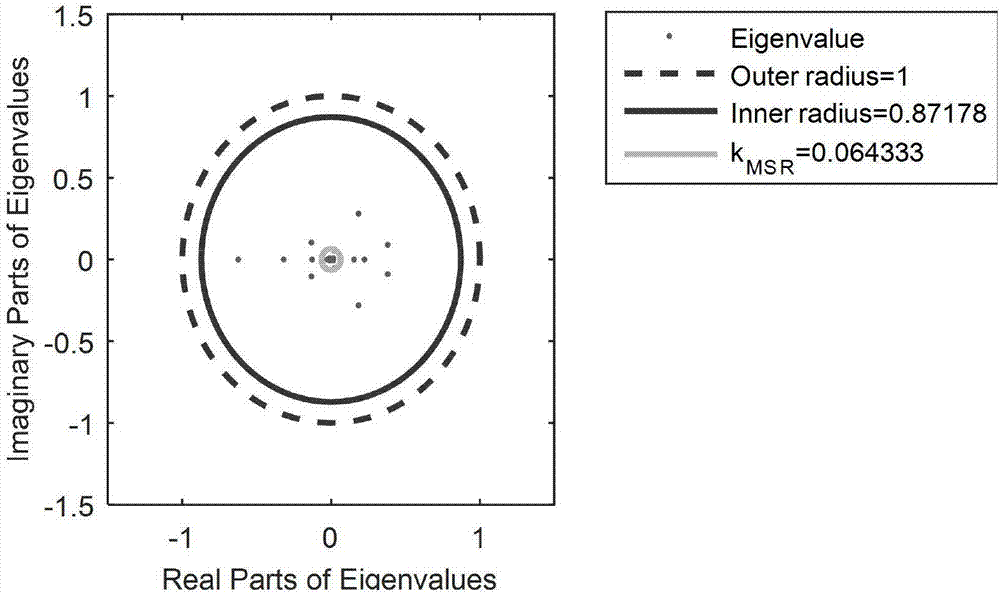
[0061] For example, in the simulation experiment, the time series V comes from the data points generated by the variable y in different chaotic systems, and the size of the matrix X is 120×500, so c=M / N=0.24;

[0062] Because the amount of data that may be obtained during actual use will be relatively small. In the case of a small amount of data, the acquired data can only constitute...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a method for recognizing chaotic time series based on the random matrix theory. The method comprises the specific steps of A, randomly selecting a time series to be recognized, and constructing original matrix X according to the time series; B, normalizing the matrix X, converting it into a non-Hermite matrix, shown in the description, having a row vector average of 0 and a variance of 1; C, calculating the non-Hermite matrix to obtain its singular value equivalent matrix X, and calculating the singular value equivalent matrix X to obtain a standard matrix product shown in the description; D, calculating according to the standard matrix product to obtain its characteristic values, and calculating an average spectral radius of the characteristic values; E, recognizing the time series as a noise time series or a chaotic time series according to the single ring law in the random matrix theory. Short chaotic time series or noise-containing chaotic time series can be recognized through the method, and subsequent research is thus facilitated; the method has a simple processing procedure and is good in universality and robustness.

Description

technical field [0001] The invention relates to a method for identifying chaotic time series, in particular to a method for identifying chaotic time series based on random matrix theory. Background technique [0002] Chaotic time series generally exist in the fields of physics, communication, biology, meteorology and economy. Because the time series generated by chaotic dynamical systems and the noise time series generated by random processes have similar time-domain irregular behavior and spectral characteristics, it is difficult to distinguish them. How to effectively identify chaotic time series and noise time series not only has theoretical significance, but also has good engineering practical value. [0003] The general methods for identifying chaotic time series are divided into qualitative and quantitative methods. The qualitative method mainly confirms whether the system is chaotic by comparing the time-frequency domain characteristics of chaotic signal and noise. ...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): G06F17/16
CPCG06F17/16
Inventor 叶宾刘鹏郭阳全王瀚洋
Owner CHINA UNIV OF MINING & TECH
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com