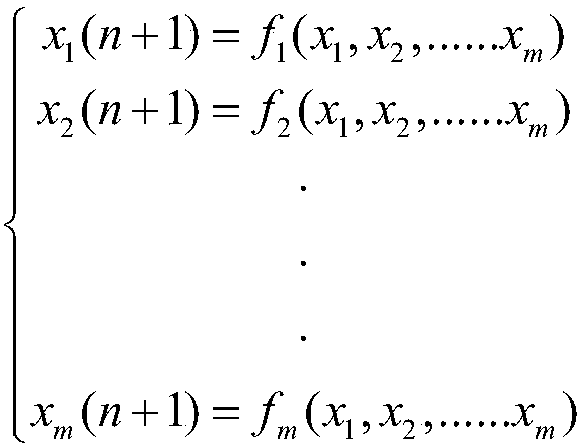Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Method for generating chaotization and chaotic sequence of high-dimensional power system

A technology of dynamic system and chaotic sequence, applied in the field of information security, can solve the problems of difficult control of Lyapunov exponent, difficult design of high-dimensional hyperchaotic system, etc., and achieve the effect of precise control

Active Publication Date: 2018-10-30
HEILONGJIANG UNIV
View PDF6 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0027] Based on the above problems, a method of chaoticization of high-dimensional dynamical system and its chaotic sequence generation method is proposed, which solves the problem that the high-dimensional hyper-chaotic system is difficult to design and the Lyapunov exponent in the chaotic system is difficult to control. This method can well control all Designing all Lyapunov exponents in a chaotic system

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Method for generating chaotization and chaotic sequence of high-dimensional power system
  • Method for generating chaotization and chaotic sequence of high-dimensional power system
  • Method for generating chaotization and chaotic sequence of high-dimensional power system

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

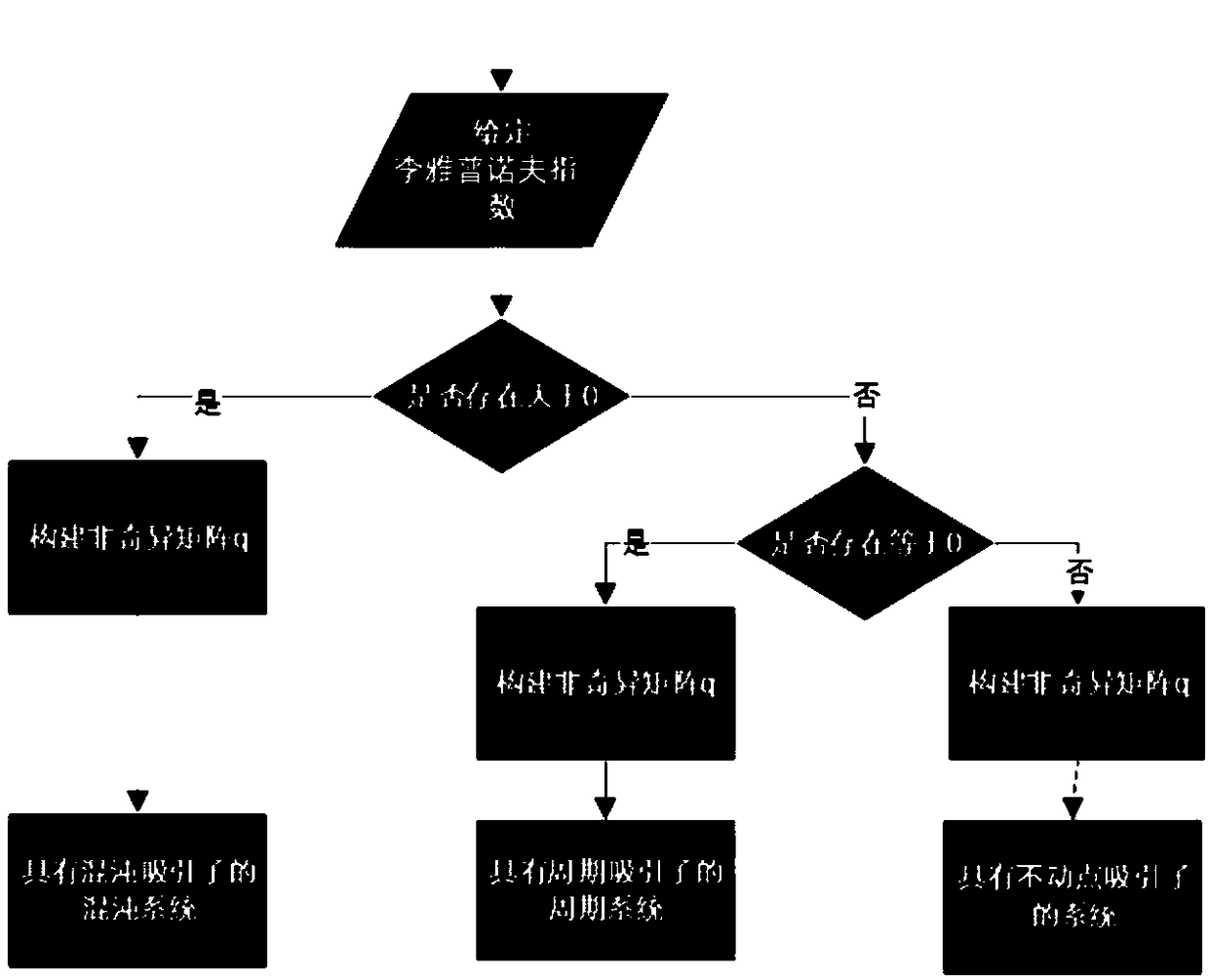
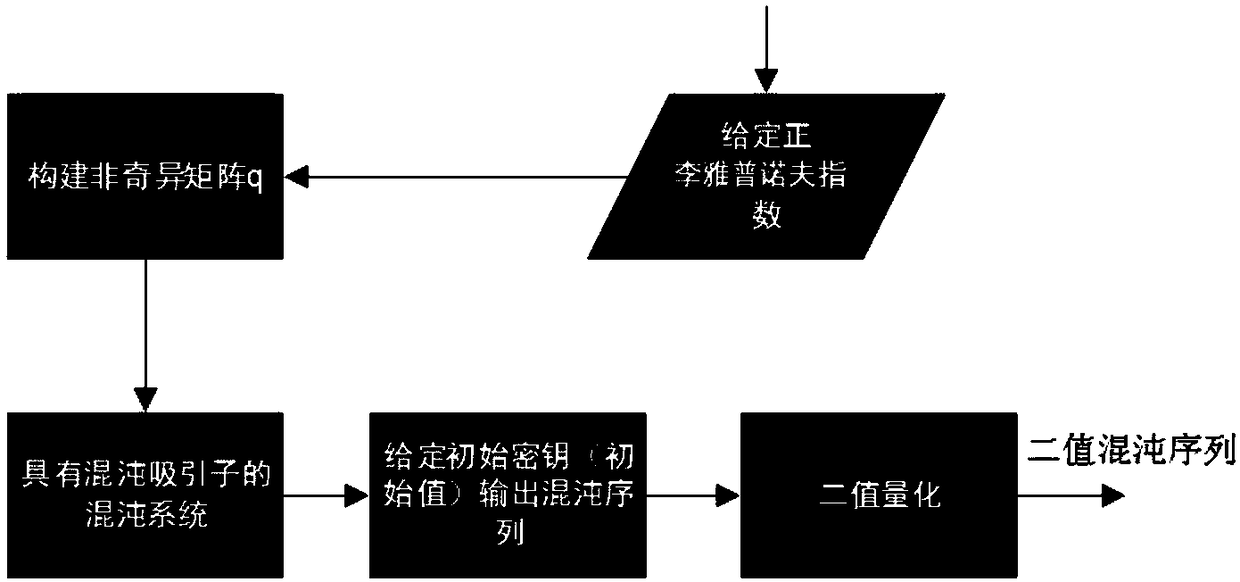
[0046] like Figure 1-2 As shown, the chaoticization of a high-dimensional dynamic system and its chaotic sequence generation method are as follows:

[0047] Let m-dimensional discrete dynamical system

[0048] S n+1 =AS n modc

[0049] where S n is the state vector (x 1 (n),x 2 (n),x 3 (n)......x m (n)) T , A is a constant coefficient matrix,

[0050]

[0051] Since there are no nonlinear terms in the m-dimensional discrete dynamical system, the Jacobian matrix is ​​A, therefore, P=A n , let the m eigenvalues ​​of matrix A be λ 0 ,λ 1 ,...,λ m , the m Lyapunov exponents in m-dimensional discrete chaos are:

[0052]

[0053] Therefore, the eigenvalues ​​of the parameter matrix A determine the Lyapunov exponent of the system; the construction method of the parameter matrix A is as follows:

[0054] (1) Given the Lyapunov exponent value LE 1 ,LE 2 ,...LE m , and calculate the eigenvalues The eigenvalue-based diagonal matrix Λ is constructed as

[0055] ...

Embodiment 2

[0060] 1. Any given 8 eigenvalues ​​greater than 1, such as 40, 41, 42, 43, 44, 45, 46, 47, and c is defined as 1. The rounded Lyapunov exponents are 3.69, 3.71, 3.74, 3.76, 3.78, 3.81, 3.83, 3.85.

[0061] 2. A nonsingular matrix q is defined as:

[0062]

[0063] The element q(i,i)=2, i=1,2,3...m, and the remaining elements are all 1. It is easy to show that q is a nonsingular matrix. When m=8, q can be defined

[0064]

[0065] and the rounded inverse matrix q -1 for

[0066]

[0067] 3. The parameter matrix is

[0068]

[0069] Reconstructing discrete dynamical systems.

[0070]

[0071] (4) The initial value of the state vector is used as the initial key, and the chaotic sequence is generated by reconstructing the discrete dynamic system. When the output sequence is greater than 0.5, the quantization is 1, and when the output sequence is less than 0.5, the quantization is 0.

Embodiment 3

[0073] The effect of the present invention can be further illustrated by the following detection results of the present embodiment:

[0074] 1. Detection method and content:

[0075] The randomness of the chaotic sequence output by the chaotic sequence generator in Embodiment 2 of the present invention is detected by using the SP800-22 random number detection standard provided by the National Institute of Standards and Technology NIST. The detection standard includes 15 detection contents, each of which is A P-value is included in the test results produced by the test. When the P value is greater than 0.01, it means that the test content has passed.

[0076] 2. Test results:

[0077] Referring to Example 2, make it generate 100 groups of 10,000,000 random sequences, and use the SP800-22 random number detection standard provided by the National Institute of Standards and Technology (NIST) for detection. One group of results is shown in Table 1-8:

[0078] Table 1x 1 (n) Out...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a method for generating chaotization and a chaotic sequence of a high-dimensional power system. The method includes the following steps that an m-dimensional discrete power system is set, Sn+1=ASnmodc, A is a constant-coefficient matrix, as no non-linear term is arranged in the m-dimensional discrete power system, the jacobian matrix is A, P=An, and the characteristic values of the parameter matrix A decide Lyapunov indexes of the system; the Lyapunov index values LE1, LE2, ..., LEm are given, the characteristic values are calculated, and a m*m-dimensional non-singularmatrix q is designed; the parameter matrix A=qGammaq-1 is calculated and put in an original model, and the discrete power system is re-constructed; the initial value of a state vector serves as an initial secret key, and a random sequence is generated through a time sequence of the re-constructed discrete power system. The Lyapunov indexes can be precisely controlled, a period system with period attractors and a system with fixed point attractors are achieved, and the chaotic sequence output through the method has more complex chaos behaviors.

Description

technical field [0001] The invention relates to the field of information security, in particular to a chaotic high-dimensional dynamic system and a method for generating chaotic sequences. Background technique [0002] Existing general chaotic design methods mainly rely on the Chen-Lai algorithm, given the initial state x 0 , for the control system x 1 =f 0 (x 0 )+B 0 x 0 Calculate its Jacobian matrix [0003] J 0 (x 0 )=f 0 '(x 0 )+B 0 x 0 , [0004] And note T 0 =J 0 (x 0 ). take B 0 x 0 =σ 0 I and choose the constant σ 0 > 0 so that the matrix [T 0 T 0 T ] is limited and diagonally dominant. For k=0,1,2,..., consider the control system [0005] x k+1 =f k (x k )+B k x k , [0006] where B k x k =σ k I has been obtained from the previous step. Now do the following calculation: [0007] Step 1. Calculate the Jacobian matrix [0008] J k (x k )=f k '(x k )+B k x k [0009] mark T k =J k T k-1 . [0010] Step 2. Choose consta...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): H04L9/00
CPCH04L9/001
Inventor 丁群王传福
Owner HEILONGJIANG UNIV
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com