Space circular arc interpolation method of triaxial cartesian robot

A rectangular coordinate, space arc technology, applied in the direction of manipulators, program-controlled manipulators, manufacturing tools, etc., can solve problems such as complex calculation, achieve the effect of simple solution, reduce steps, and improve operation speed

Inactive Publication Date: 2019-01-11
NANJING UNIV OF INFORMATION SCI & TECH
View PDF5 Cites 8 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0004] Existing techniques for judging the relationship between the center angle of a supplementary arc and the angle between two vectors include: separately calculating the angles from the starting point to the passing point, and from the passing point to the end point, and then summing them up. This requires three steps of calcul

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Space circular arc interpolation method of triaxial cartesian robot
  • Space circular arc interpolation method of triaxial cartesian robot
  • Space circular arc interpolation method of triaxial cartesian robot

Examples

Experimental program
Comparison scheme
Effect test

Embodiment Construction

[0050] The technical solutions of the present invention will be described in detail below in conjunction with the accompanying drawings.

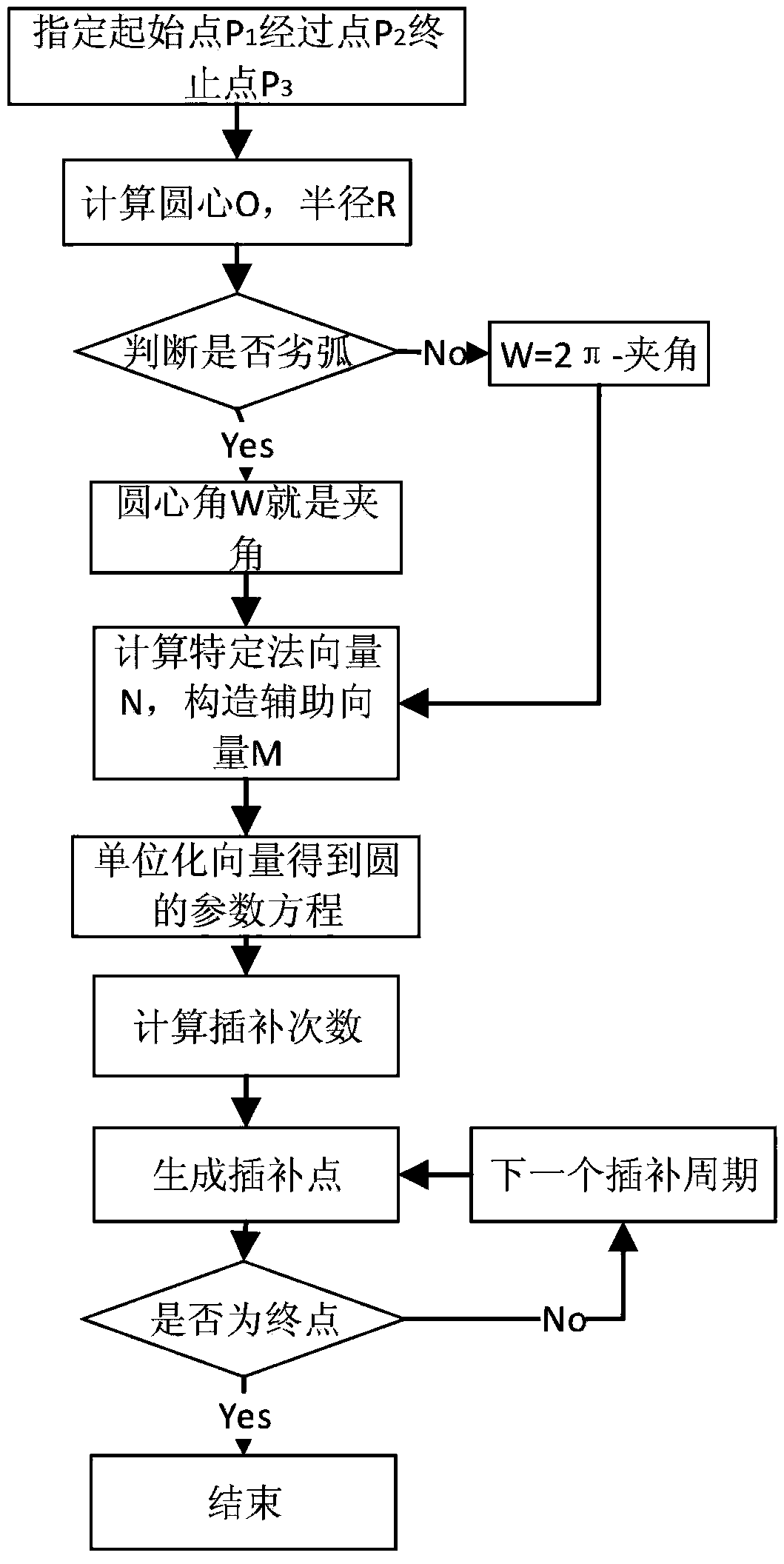
[0051] The space circular interpolation method of a kind of three-axis Cartesian coordinate robot space arc interpolation method designed by the present invention, such as figure 1 As shown, the specific process is as follows.

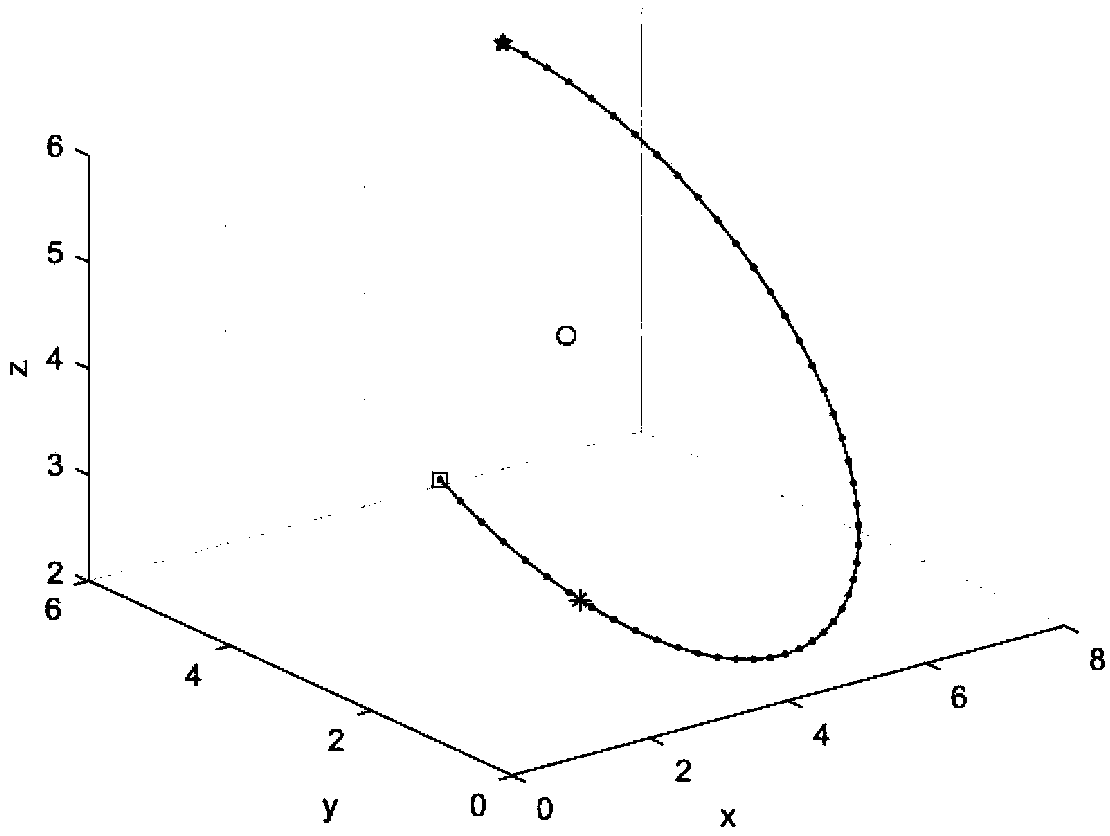
[0052] S01, specify any 3 points that are not collinear through the teaching pendant or other host computer: starting point P 1 (1,2,4), through point P 2 (2, 1, 3), end point P 3 (6,6,6).

[0053] S02, substitute three points into the center of the circle O(o x ,o y ,o z ), the analytical formula of radius R, which is obtained by solving the two constraints of three points being coplanar and three points being equal to the center of the circle;

[0054] A 1 =y 1 *z 2 -y 1 *z 3 -z 1 *y 2 +z 1 *z 2 +y 2 *z 3 -z 2 *z 2 = 2;

[0055] B 1 =-x 1 *z 2 +x1*z 3 +z 1 *x 2 -z 1 *z 1 -x 2 *z 3 +z...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to view more

PUM

No PUM Login to view more

Abstract

The invention discloses a space circular arc interpolation method of a triaxial cartesian robot. The space circular arc interpolation method of the triaxial cartesian robot comprises the steps that any three non-collinear points on the movement path of the triaxial cartesian robot are designated; the three points are substituted into an analysis formula of the circle center and the radius; the central angle of the circular arc needing interpolation is calculated; the specific normal vector N of the plane where the three points are located is calculated, and a specific auxiliary vector M is constructed according to the normal vector N; the parameter equation of the interpolation points are expressed; the number of times of interpolation is calculated; the parameter value of the ith interpolation is calculated and substituted into the parameter equation, and the point coordinates of the ith interpolation are obtained; the termination point of interpolation is judged; and a calculation result is transmitted to an execution mechanism of the triaxial cartesian robot. The space circular interpolation method of the triaxial cartesian robot reduces the calculation amount, simplifies the code quantity, improves the operation speed and the interpolation precision, is suitable for any starting and termination points and any plane and can be applied to the robot control field having higherrequirements for the operation speed and the precision.

Description

technical field [0001] The invention belongs to the technical field of robot control, and in particular relates to a space circular interpolation method for a three-axis Cartesian coordinate robot. Background technique [0002] In today's applications in the field of robot control, such as dispensing and engraving of three-axis Cartesian robots, trajectory planning is the key to completing the task. Circular interpolation is one of the main tasks of trajectory planning. Usually, only a few key points on the motion path are given, and intermediate points are interpolated according to the characteristics of the trajectory, so as to achieve high-precision motion control in colleges and universities. These systems need to achieve real-time processing, and need a method with simple algorithm, low calculation amount, fast operation speed and high accuracy of interpolation coordinates. [0003] The existing technology needs to judge the interpolation direction, and the judgment me...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to view more

Application Information

Patent Timeline
no application Login to view more
IPC IPC(8): B25J9/16
CPCB25J9/1664
Inventor 李涛江磊贾忠益
Owner NANJING UNIV OF INFORMATION SCI & TECH
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Try Eureka
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap