Method for calculating optimal single-strand diameter and number of strands of square litz wire under non-sinusoidal current waveform excitation
A technology of shaped litz wire and current waveform, which is applied in the field of calculation of optimal single strand diameter and number of strands of square litz wire under non-sinusoidal current waveform, can solve the problem of no litz wire AC loss calculation method, reduced analytical accuracy, litz wire structure Complicated problems, to achieve the effect of benefiting engineering applications, reducing calculation workload, and saving calculation time
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
Image
Examples
Embodiment Construction
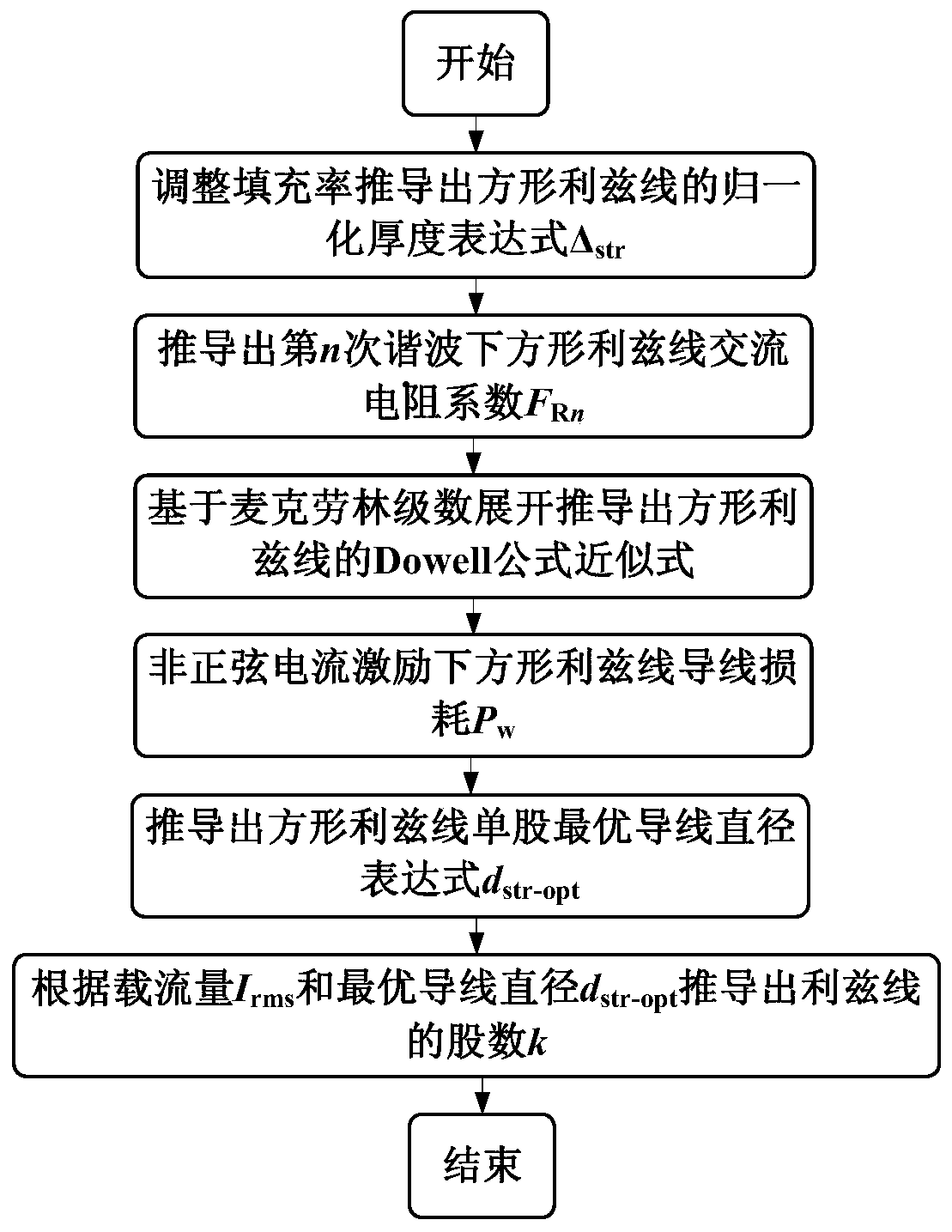
[0036] Below in conjunction with accompanying drawing and specific embodiment the present invention will be further described as follows:
[0037] figure 1 It is a flow chart of the method for calculating the optimal single-strand diameter and strand number of a square litz wire under non-sinusoidal current waveform excitation of the present invention, including the following steps:
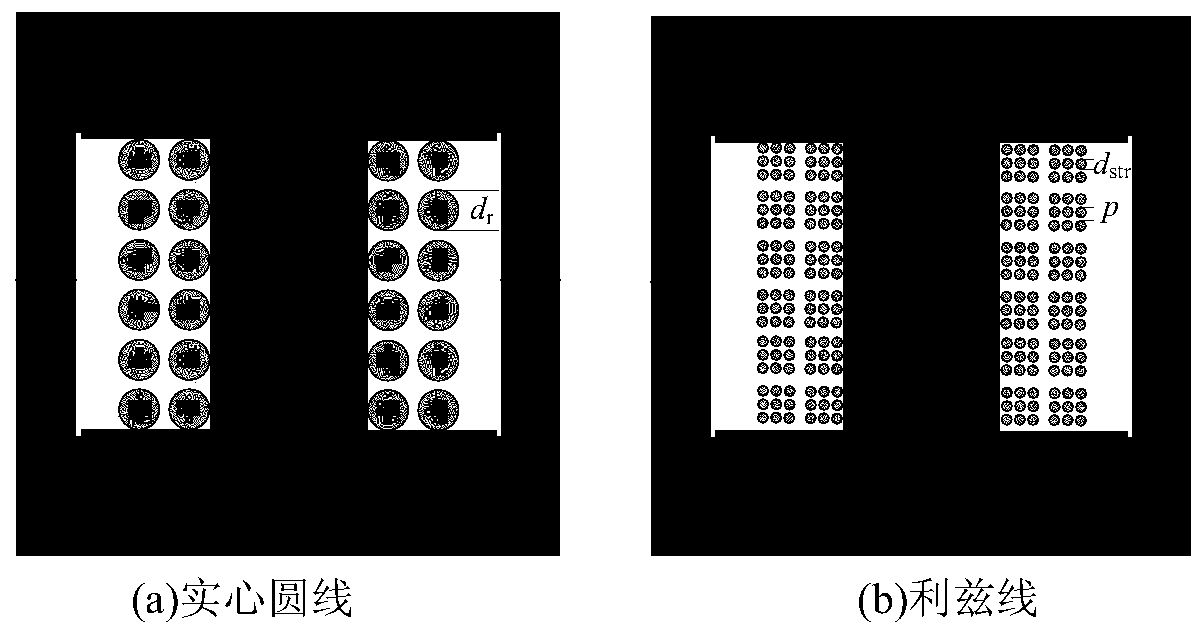
[0038] Step 1: Combining the filling rate of each layer of the square litz wire, derive the normalized thickness expression Δ of the square litz wire str .
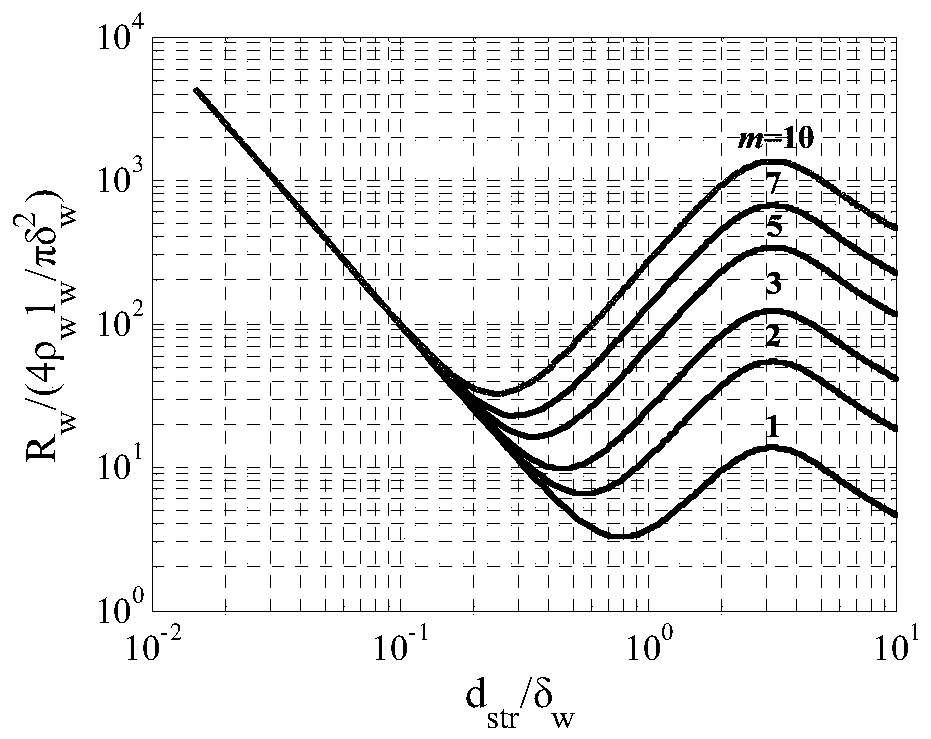
[0039] Step 2: Combining the Dowell equation to derive the AC resistivity expression F of the square Litz wire at the nth harmonic frequency Rn .
[0040] Step 3: Using McLaughlin series expansion, the low frequency condition (d str / δ w ≤2), the approximate expression of the Dowell formula of the square Litz wire.
[0041] Step 4: Derive the loss P of the square litz wire under non-sinusoidal current excitation w .
[0042] Step 5: ...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - Generate Ideas
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com