Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Method and system for quickly calculating size of maximum connected subgraph

A technology of maximum connected subgraph and fast calculation, applied in the field of graph theory and complex network computing, it can solve problems such as inconvenient computer implementation, calculation, and inability to find the maximum connected subgraph.

Inactive Publication Date: 2019-10-18
GUANGZHOU UNIVERSITY
View PDF0 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0004] The above calculation methods usually start from the correlation between points and use the traversal algorithm to judge the connectivity between nodes. Usually, this kind of algorithm can only judge the connectivity of the graph, and cannot find the largest connected subgraph and calculate Its largest connected subgraph size
In addition, most of these calculation methods are algorithms that are difficult to understand or explain, or are not convenient for computer implementation, which brings certain difficulties to learners in the industry

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Method and system for quickly calculating size of maximum connected subgraph
  • Method and system for quickly calculating size of maximum connected subgraph
  • Method and system for quickly calculating size of maximum connected subgraph

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

[0030] see figure 1 , a fast calculation method for the size of the largest connected subgraph, including:

[0031] S1, set the shortest distance matrix D for a graph G containing n nodes n×n ; Specifically, preset d ij The shortest distance matrix is ​​D n×n elements in , where d ij is the shortest distance from point i to point j in graph G, then step S1 includes: if point i cannot reach j, then the shortest distance d from point i to point j ij = inf, where inf is positive infinity; if point i can reach j, then the shortest distance d from point i to point j ij is a constant; if i=j, the shortest distance d ii =0. Among them, graph G is a fully connected graph.

[0032] S2, according to the transformation formula, the shortest distance matrix D n×n Transformed into a reachable matrix A n×n ; The transformation formula is:

[0033]

[0034] Among them, a ij is reachable matrix A n×n Elements.

[0035] S3, will reach matrix A n×n The vectors of are divided in...

Embodiment 2

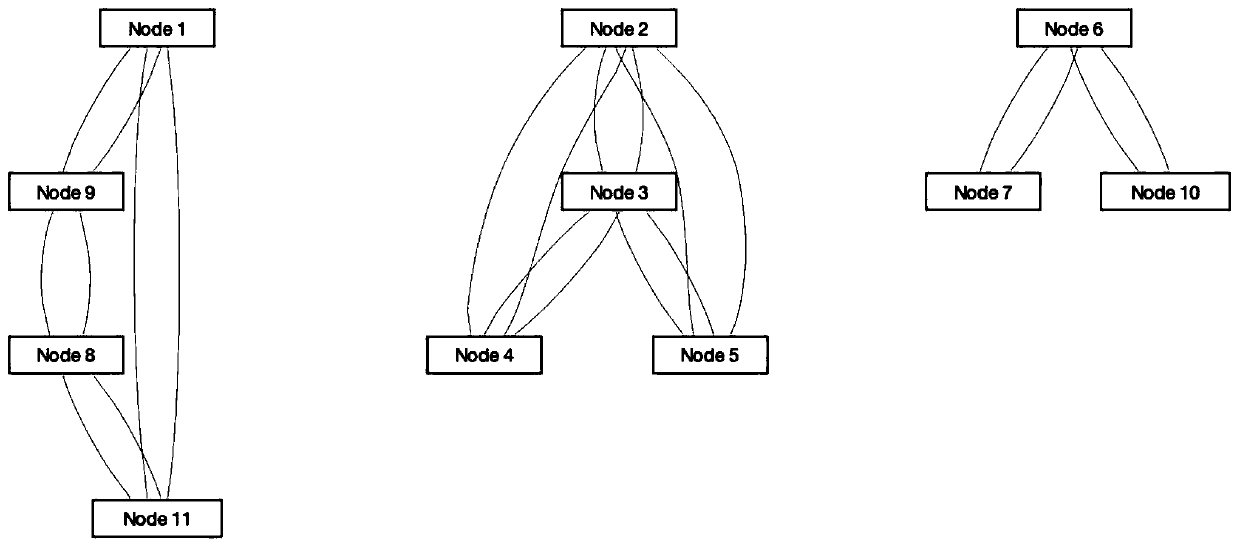
[0053] The difference between this embodiment and embodiment 1 is that, see Figure 4 , graph G is an unweighted directed graph G containing three subgraphs: According to step S1, its shortest distance matrix D is obtained n×n for:

[0054]

[0055] Among them, in this embodiment, when point i can reach j, then the shortest distance d from point i to point j ij for 1 or 2 or 3.

[0056] According to the transformation formula, the reachable matrix is ​​as follows:

[0057]

[0058] Next, the reachable matrix A n×n Classify, the present embodiment can be divided into six classes, as follows:

[0059]

[0060] Among them, capacity i k They are 4, 3, 1, 1, 1, 1 respectively, and there is a maximally connected subgraph whose node numbers (serial numbers corresponding to column vectors) are 1, 8, 9, 11, from which the maximally connected subgraph of graph G can be calculated The size of the subgraph is G=max(i k ) / n=4 / 11=0.3637, max(i k ) is 4.

[0061] In summary...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a method for quickly calculating the size of a maximum connected subgraph. The method comprises the following steps: S1, setting a shortest distance matrix Dn * n of a graph Gcontaining n nodes; S2, converting the shortest distance matrix Dn * n into a reachable matrix An * n according to a conversion formula; S3, dividing the vectors of the reachable matrix An * n into kclasses according to a preset classification rule, wherein the row and column number of the vectors in each class is used as the capacity ik, and k is larger than or equal to 1; and S4, judging the size of the maximum connected subgraph according to the maximum value of each type of capacity ik. According to the scheme, the reachable matrix is obtained by utilizing the shortest distance matrix, and the maximum communication size is directly identified from the reachable matrix, so that the situation that all nodes need to be traversed in traditional maximum communication sub-graph size calculation is avoided, and the scheme not only reduces complex calculation, but also is convenient to implement.

Description

technical field [0001] The invention relates to the technical field of graph theory and complex network computing, in particular to a method and system for fast computing the size of the largest connected subgraph, which is applicable to computing problems in multiple fields such as operations research, network theory, information theory, cybernetics, and game theory . Background technique [0002] Graph theory is widely used in operations research, network theory, information theory, cybernetics, game theory and many other fields. Graph theory in particular is applied and plays a key role in many areas of computer science. For example, graph theory plays an important role in switch theory and logic design, data structure, formal language and automata, operating system, compiler programming, and information organization and retrieval. The connectivity of graphs is a basic concept in graph theory, which is used almost everywhere. Because of this, connectivity occupies a pi...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): G06F16/901G06F16/906
CPCG06F16/9024G06F16/906
Inventor 李乙侠李树栋吴晓波韩伟红方滨兴田志宏殷丽华陈燕珊卢丹娜王薇郑敏真何沛言顾钊铨仇晶李默涵唐可可
Owner GUANGZHOU UNIVERSITY
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com