Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Back-step self-adaptive fuzzy sliding-mode control method of under-actuated aerial autonomous underwater vehicle (AUV) under composite disturbance

An adaptive fuzzy and backstepping sliding mode technology, applied in the direction of adaptive control, general control system, control/regulation system, etc., can solve the problems of not considering the uncertainty of external disturbance parameters, ignoring the dynamic characteristics of underactuated AUVs, etc. , to achieve the effect of good composite interference, high stability and precise tracking effect

Active Publication Date: 2019-12-27
HARBIN ENG UNIV
View PDF6 Cites 10 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0004] At present, most of the research on AUV control at home and abroad is based on the controller design of the nominal model, ignoring the dynamic characteristics of the underactuated AUV itself, and not considering the influence of external disturbance and parameter uncertainty.

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Back-step self-adaptive fuzzy sliding-mode control method of under-actuated aerial autonomous underwater vehicle (AUV) under composite disturbance
  • Back-step self-adaptive fuzzy sliding-mode control method of under-actuated aerial autonomous underwater vehicle (AUV) under composite disturbance
  • Back-step self-adaptive fuzzy sliding-mode control method of under-actuated aerial autonomous underwater vehicle (AUV) under composite disturbance

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

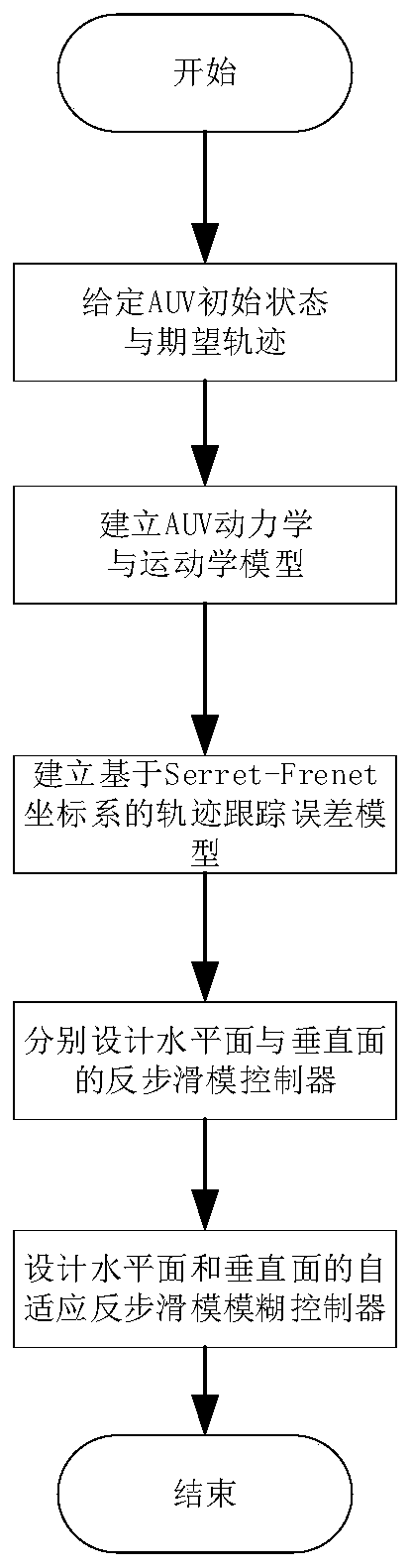
[0088] Implementation 1: If figure 2 It is a flow chart of adaptive backstepping sliding mode fuzzy control, and its implementation process is:

[0089] Step 1, establishing the dynamics and kinematics models of the vertical and horizontal planes of the AUV;

[0090] Step 2, establishing a trajectory tracking error model based on the Serret-Frenet coordinate system;

[0091] Step 3: Using the error variable and dynamic model described above, construct a backstepping sliding mode control controller for the horizontal plane and the vertical plane respectively, and obtain the controller outputs under the horizontal plane and the vertical plane respectively, so as to realize the underactuation under the condition of no disturbance AUV trajectory tracking control;

[0092] Step 4, adding an adaptive fuzzy control system to the trajectory tracking controller under the aforementioned disturbance-free control, so as to realize the identification and suppression of compound disturba...

Embodiment 2

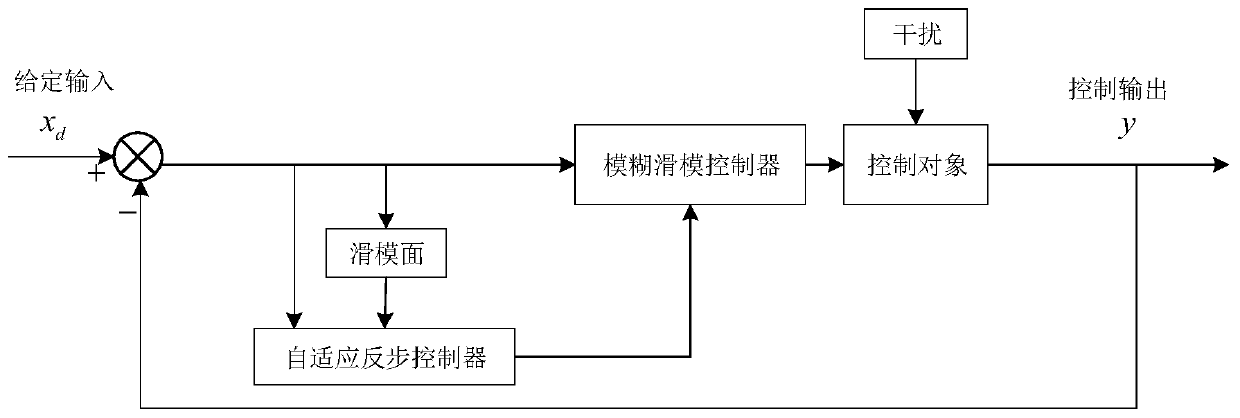
[0093] Implementation 2: If image 3 It can be seen that it mainly includes fuzzy sliding mode controller, adaptive backstepping controller and control object. The present invention establishes the kinematics and dynamics model of AUV:

[0094] The kinematic equation of the horizontal plane is:

[0095]

[0096] The kinematic equation of the vertical plane is:

[0097]

[0098] The horizontal dynamic equation is:

[0099]

[0100] The dynamic equation of the vertical plane is:

[0101]

[0102] Then the tracking error model is established in the Serret-Frenet coordinate system:

[0103] The tracking error equation of AUV horizontal plane trajectory is:

[0104]

[0105] The AUV vertical surface trajectory tracking error equation is:

[0106]

Embodiment 3

[0107] Implementation 3: Design an adaptive backstepping controller:

[0108] Horizontal plane backstepping sliding mode longitudinal velocity controller:

[0109]

[0110] Horizontal plane backstepping sliding mode heading controller

[0111]

[0112] Vertical Backstepping Sliding Mode Pitch Angle Controller

[0113]

[0114] Apply this controller to the control object in Implementation 1, and get Figure 4 , Figure 5 . Figure 4 is the circular trajectory tracing graph in the horizontal plane, Figure 5 Trace the graph for a sinusoidal trajectory in the vertical plane. The simulation assumes that the initial conditions are the same, regardless of external interference, and the expected speed of the AUV is u d =1m / s, respectively select a circle and a sinusoidal curve as the trajectory to be tracked, and the initial state of the AUV is v(0)=r(0)=0, u(0)=0.08m / s. Depend on Figure 4 and Figure 5 It can be seen that both the horizontal plane trajectory track...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a back-step self-adaptive fuzzy sliding-mode control method of an under-actuated aerial autonomous underwater vehicle (AUV) under composite disturbance. The back-step self-adaptive fuzzy sliding-mode control method comprises the steps of building a kinematics and kinetic model of the AUV, and building a Serret-Frenet coordinate system-based track tracing error model; and respectively designing track tracking back-step sliding-mode controllers of a horizontal plane and a vertical plane under the condition that no interference is considered according to the error model soas to achieve a track tracing function. On the basis, a working state of the system under a combined interference condition is considered, a self-adaptive fuzzy logic system is additionally arrangedat an original controller, the interference-resistance capability of the system is improved, and the track tracing control of the under-actuated AUV under the condition of external composite interference is achieved. By the back-step self-adaptive fuzzy sliding-mode control method, the composite interference of the under-actuated AUV can be identified, and a reference scheme having advantages of adaptability, high robustness and the like is provided for accurate control of track tracing of the AUV.

Description

technical field [0001] The invention relates to the field of trajectory tracking control of an underwater robot, in particular to a backstep self-adaptive fuzzy sliding mode control method, which can enable the AUV to stably track a predetermined trajectory under complex disturbances. Background technique [0002] The ocean is a treasure house of vital resources on the earth. Due to the depletion of land resources, the ocean has gradually become the focus of human development. According to human detection so far, there are a large number of fossil fuels, metal deposits and biological resources in the ocean, and the ocean is also a treasure land for transportation and wave power generation. In recent years, mankind has accelerated the pace of ocean development, and various countries regard the ocean as an important field of research and development. However, the environment of the ocean is special compared to the land. The underwater environment is very harsh. As the water d...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): G05B13/02G05B13/04G05D1/10
CPCG05B13/0275G05B13/042G05D1/0088G05D1/10
Inventor 魏延辉蒋志龙贺佳林李强强马博也牛家乐刘东东姜瑶瑶
Owner HARBIN ENG UNIV
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com