Check patentability & draft patents in minutes with Patsnap Eureka AI!

Linear motion demodulation implementation method based on improved differential cross multiplication

A technology of linear motion and implementation method, applied in the field of radar detection, can solve problems affecting the robustness and anti-noise ability of the algorithm, reduce the accuracy and stability of the demodulation signal, increase the cumulative noise and approximation error of the demodulation result, and achieve Effects of high linearity, improved operating efficiency, and noise robustness

Pending Publication Date: 2020-08-07
SHANGHAI JIAO TONG UNIV
View PDF6 Cites 4 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

The DACM algorithm is realized by performing differential and integral operations on the basis of the arctangent algorithm, which causes the DACM algorithm to perform nested operations and a large number of approximations, which increases the cumulative noise and approximation error of the demodulation results and reduces the demodulation signal. accuracy and stability
In addition, both the arctangent algorithm and the DACM algorithm rely too much on the accuracy of the pre-DC offset calibration step, which affects the robustness and noise immunity of the algorithm

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Linear motion demodulation implementation method based on improved differential cross multiplication
  • Linear motion demodulation implementation method based on improved differential cross multiplication
  • Linear motion demodulation implementation method based on improved differential cross multiplication

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

[0023] small motion detection

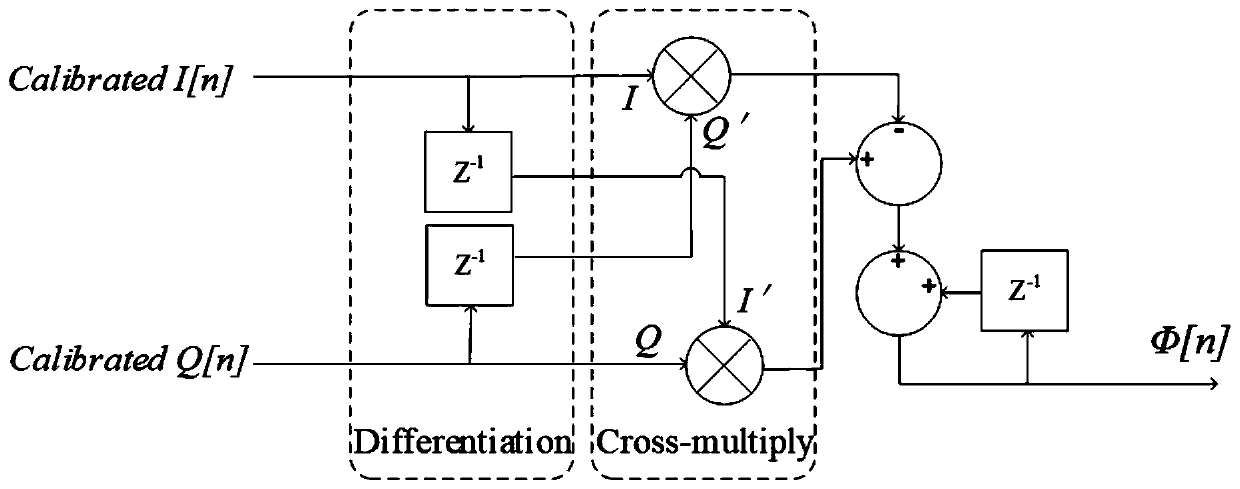
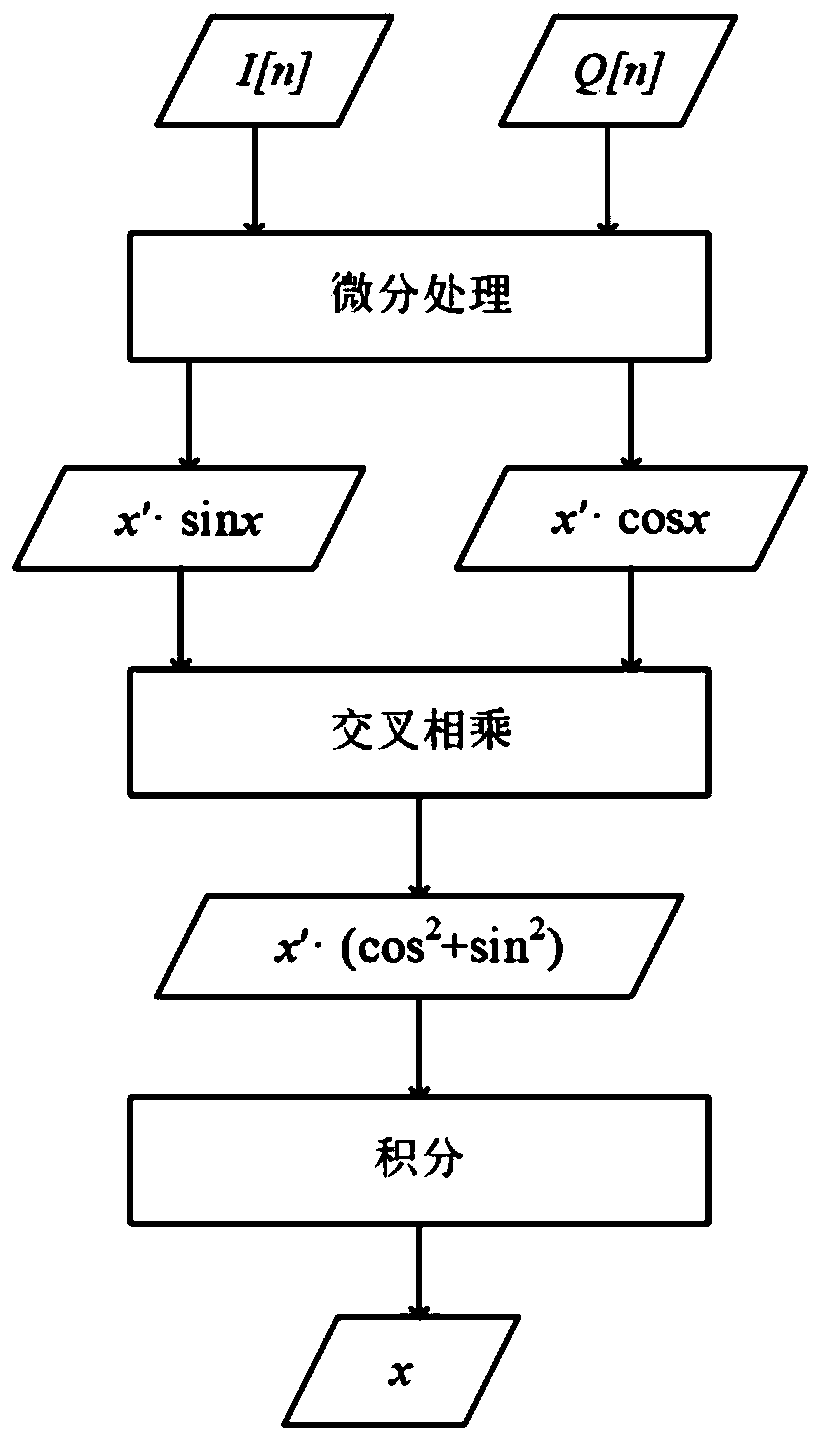
[0024] In this embodiment, a 2.4GHz radar sensor system is used to detect the mechanical movement of the target object within 10mm. Based on the geometric theorem of trigonometric functions, without arctangent transformation, the calibration signal is directly cross-multiplied to realize demodulation of motion information. for:

[0025] Step ① Differentiate the calibration signal directly in the time domain to obtain:

[0026]

[0027] Step ② Use the geometric theorem cos of trigonometric functions 2 Φ+sin 2 Φ=1, directly extract the motion signal to be measured from the differential result of step ①: Since the signal in the differential form is susceptible to noise interference and is not conducive to the processing of subsequent circuits, the motion signal to be measured is restored to the motion signal in the digital domain in a further step, and the final digital algorithm expression is obtained:

[0028] The experimental results...

Embodiment 2

[0030] large motion detection

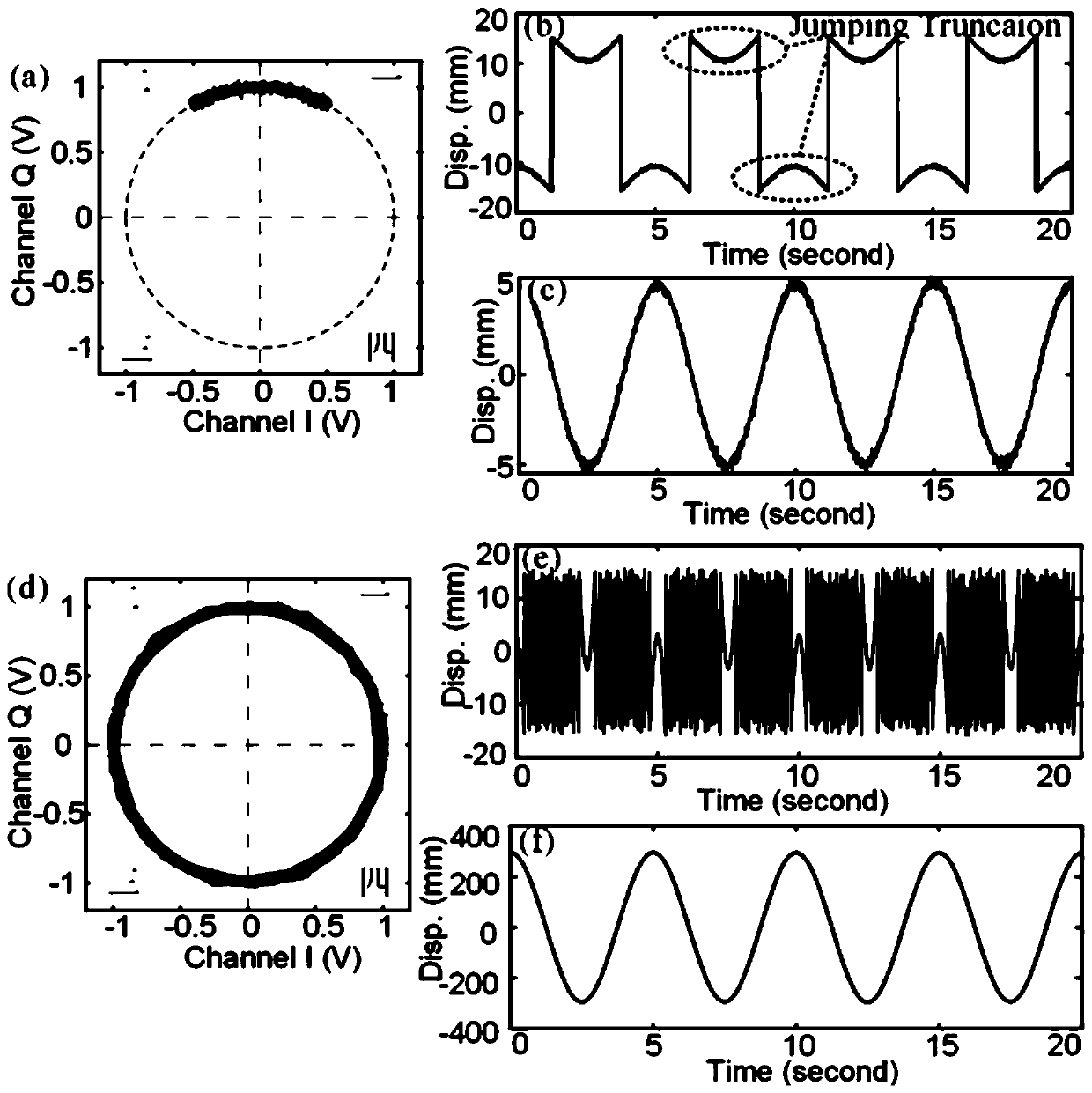
[0031] In this embodiment, a 120GHz radar detection module with a wavelength of only 2.5mm is used to measure large-scale motion signals. Except for small-amplitude motions that are not within the value range, large-displacement motions will also cause phase aliasing and phase ambiguity. exist image 3 In (a)-(c), the I / Q signal phase trajectory spans the first and second quadrants and the trajectory range is less than π / 2. In this case, the motion signal reconstructed by arctangent algorithm has phase ambiguity, but the demodulated signal obtained by this method has no phase distortion. In addition, when the I / Q phase trajectory is far beyond 2π, such as image 3 As shown in (d)-(f), the phase discontinuity appears again in the arctangent demodulation result. On the contrary, this method can still maintain the high linearity, authenticity and integrity of the target motion information.

[0032] In this embodiment, based on the geometric the...

Embodiment 3

[0039] Motion Information Demodulation Simulation under Loud Noise

[0040] The traditional DACM algorithm performs arctangent transformation on Q / I as a whole, and performs differentiation and cross multiplication on this basis, which introduces a large number of approximation errors and cumulative noise during the operation process, which seriously affects the anti-noise ability of the algorithm. In addition, higher requirements are placed on the accuracy of the pre-calibration steps. In contrast, the DACM algorithm in this method has a more streamlined expression, which greatly reduces the number of operations and approximation errors, and optimizes the stability and anti-noise ability of the demodulation process. Figure 4 It is the demodulated signal obtained by each algorithm under 25dB SNR. It can be seen that compared with the existing DACM algorithm, the arctangent algorithm has the smallest variance, and the algorithm proposed by this method also has high stability ...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a linear motion demodulation implementation method based on improved differential cross multiplication. The method comprises the steps: based on trigonometric function geometric theorem, directly carrying out the differential processing on the I / Q signal without arc tangent transformation after direct current calibration; carrying out cross multiplication and logic additionoperation with an original I / Q signal. According to the method, the difference and trigonometric function geometric theorem is utilized, arc tangent transformation is not carried out, only first-order operation of the I / Q signals is involved, the operation process is greatly simplified, the operation approximation and accumulated noise are reduced, and the algorithm linearity, stability and anti-noise capacity are improved.

Description

technical field [0001] The invention relates to a technique in the field of radar detection, in particular to a method for implementing linear motion demodulation based on improved differential cross multiplication. Background technique [0002] In the radar detection target trajectory, signal processing technology based on phase information is needed. The target motion causes the nonlinear phase modulation of the radar electromagnetic wave signal, so a high linearity demodulation method must be used. Currently the most commonly used linear demodulation algorithms are the arctangent algorithm and the differential cross multiplication (DACM) algorithm. First of all, the arctangent algorithm is simple and has high linearity, which once attracted widespread attention of linear demodulation. However, the arctangent algorithm has strict value range constraints on the motion signal to be measured, which affects the universal application of the algorithm. When the motion informa...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): G01S7/41
CPCG01S7/415
Inventor 顾昌展徐炜毛军发
Owner SHANGHAI JIAO TONG UNIV
Features
  • R&D
  • Intellectual Property
  • Life Sciences
  • Materials
  • Tech Scout
Why Patsnap Eureka
  • Unparalleled Data Quality
  • Higher Quality Content
  • 60% Fewer Hallucinations
Social media
Patsnap Eureka Blog
Learn More

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com