Method for solving time-varying continuous algebraic Riccati equation based on zero neural network

A neural network algorithm and neural network technology, applied in neural learning methods, biological neural network models, neural architectures, etc., can solve the problems of low accuracy, slow convergence speed, and high complexity, and achieve the effect of strong robustness

Pending Publication Date: 2021-08-20
GUANGDONG OCEAN UNIVERSITY
View PDF0 Cites 2 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0003] The purpose of the present invention is to provide a method based on error-based adaptive coefficient zeroing neural network for solving time-varying continuous algebraic Riccati equations, which solves the problems of traditional algorithms that cannot be solved due to time-varying continuous algebraic problems, high complexity, and slow convergence speed , low precision and other issues

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Method for solving time-varying continuous algebraic Riccati equation based on zero neural network
  • Method for solving time-varying continuous algebraic Riccati equation based on zero neural network
  • Method for solving time-varying continuous algebraic Riccati equation based on zero neural network

Examples

Experimental program
Comparison scheme
Effect test

specific example

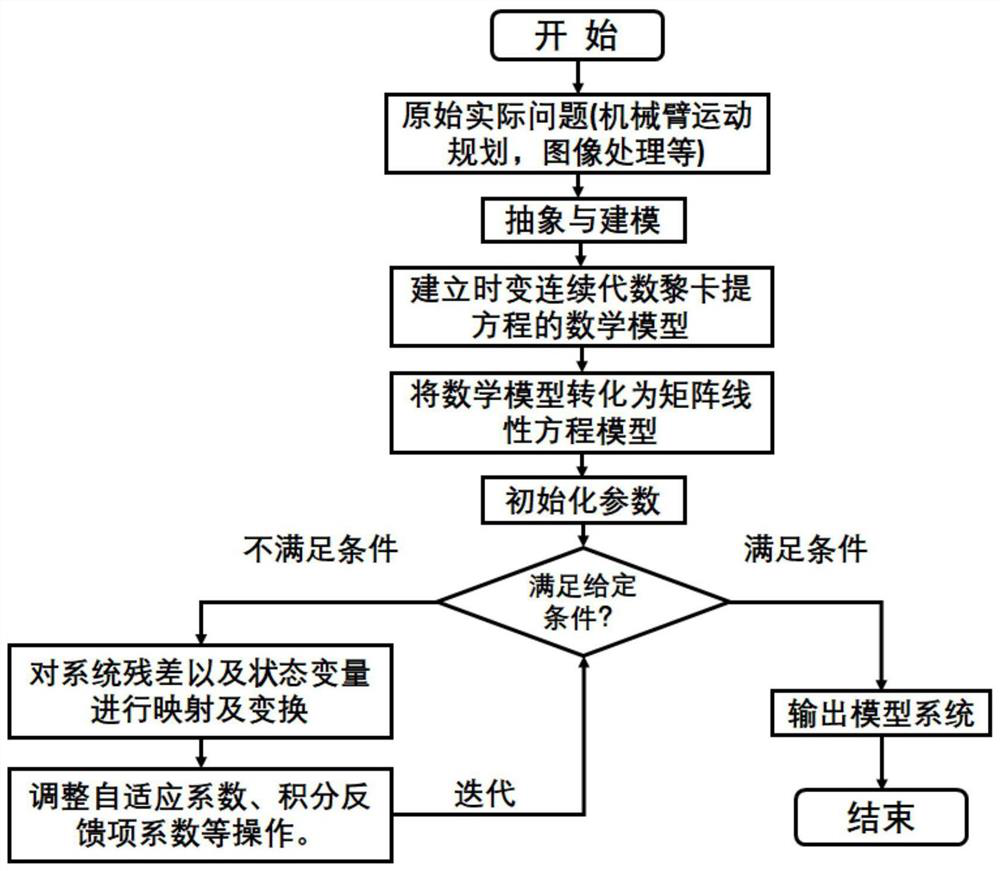
[0108] First, pass in the instance of the matrix, the specific example is as follows:

[0109]

[0110]

[0111]

[0112] Given adaptive parameters

[0113]

[0114] Coefficient for the given feedback integral term

[0115] μ=5

[0116] given noise

[0117] A. Constant noise: ξ(t)=[2] 4

[0118] B. Linear noise: ξ(t)=[0.4×t] 4

[0119] C. Random noise: ξ(t)∈[0.5, 2] 4

[0120] Secondly, according to the given example, the time-varying continuous algebraic Riccati equation is incorporated into the error-based adaptive coefficient zeroing neural network solution framework, and the formula is defined according to the evolution of the error-based adaptive coefficient zeroing neural network

[0121]

[0122] Derive an iterative model for solution.

[0123] Finally, the iterative model is calculated using a differential equation solver until the predetermined conditions are met.

[0124] figure 2 , image 3 and Figure 4 It shows the simulation results o...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to view more

PUM

No PUM Login to view more

Abstract

The invention discloses a method for solving a time-varying continuous algebraic Riccati equation based on an error adaptive coefficient zero neural network, which comprises the following steps: firstly, abstracting and modeling original problems, such as mechanical arm motion planning, image and signal processing and the like, and converting the problems into a mathematical model for solving the time-varying continuous algebraic Riccati equation; converting the mathematical model into a time-varying matrix linear equation problem through derivation and Kronecker product, using an error-based adaptive coefficient zero neural network for iterative solution, performing mapping and adaptive transformation continuously on system residual errors and state variables in the solution process, and adjusting the solution strategy of the network; finally, stopping iteration and outputting the model system when the model system obtained by iteration solution meets predefined conditions and precision. Compared with other traditional methods for solving the time-varying continuous algebraic Riccati equation, the algorithm provided by the invention has higher convergence precision and robustness.

Description

technical field [0001] The invention relates to the technical field of matrix equations and neural networks, in particular to a method for solving time-varying continuous algebraic Riccati equations by an error-based adaptive coefficient zeroing neural network (Norm-BasedAdaptionCoefficientZeroingNeuralNetwork). Background technique [0002] Time-varying continuous algebraic Riccati equation is an important branch of optimization theory. Time-varying continuous algebraic Riccati equation is widely used in scientific research and engineering applications, such as image target detection, robot kinematics, power system design, communication engineering or control In theory and other fields, it is necessary to solve the time-varying continuous algebraic Riccati equation accurately. The traditional method usually discretizes the time-domain finite-difference problem first, and then transforms it into a static finite-difference problem in each time slice to solve. However, it is ...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to view more

Application Information

Patent Timeline
no application Login to view more
Patent Type & Authority Applications(China)
IPC IPC(8): G06F17/11G06F17/16G06N3/04G06N3/08
CPCG06F17/11G06F17/16G06N3/04G06N3/08
Inventor 肖秀春姜丞泽金龙李坤键
Owner GUANGDONG OCEAN UNIVERSITY
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Try Eureka
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap