Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Hyperspectral image eigen decomposition method based on digital surface model assistance

A digital surface model and hyperspectral image technology, applied in the field of hyperspectral image eigendecomposition, can solve the problem of low precision of hyperspectral image eigendecomposition, achieve the effect of eliminating spectral information degradation and improving accuracy

Active Publication Date: 2021-09-17
HARBIN INST OF TECH
View PDF9 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0003] The purpose of the present invention is to solve the problem of low precision of the existing hyperspectral image eigendecomposition, and to provide a hyperspectral image eigendecomposition method based on digital surface model assistance

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Hyperspectral image eigen decomposition method based on digital surface model assistance
  • Hyperspectral image eigen decomposition method based on digital surface model assistance
  • Hyperspectral image eigen decomposition method based on digital surface model assistance

Examples

Experimental program
Comparison scheme
Effect test

specific Embodiment approach 1

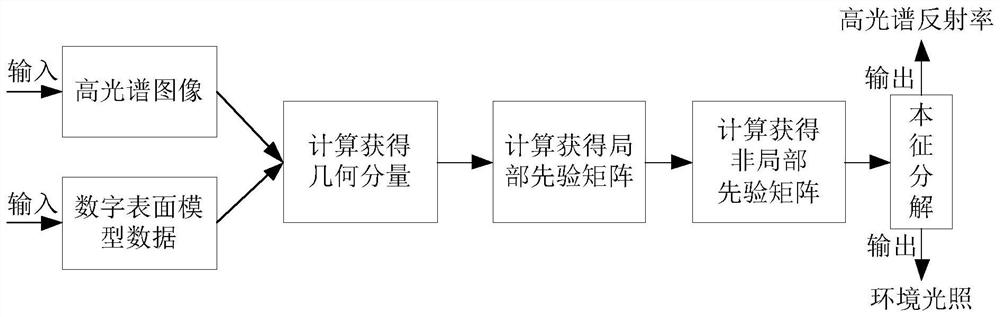
[0061] DETAILED DESCRIPTION a: below with figure 1 The present embodiment described embodiment, the present embodiment the hyperspectral image eigen decomposition model based on the digital auxiliary surface, comprising:

[0062] Sl, and a digital input hyperspectral image surface model data, geometrical components obtained by calculation;

[0063] S2, prior partial matrix obtained by calculation;

[0064] S3, obtained by calculation prior nonlocal matrix;

[0065] S4, the geometrical components, local and nonlocal priori matrix prior eigen decomposition matrix, and outputs a high spectral reflectance of ambient light.

specific Embodiment approach 2

[0066] DETAILED Embodiment 2: This embodiment of the first embodiment will be further described, particularly the S1 method of geometrical components obtained by calculation comprises:

[0067] Hyperspectral image input

[0068] Elevation data of the input digital surface model

[0069] Where H k = [H k (Λ 1 ), H k (Λ 2 ), ..., h k (Λ d )]] T , K = 1,2, ..., u represents the spectral characteristics of each pixel, k = 1,2, ..., u denotes an index of each pixel, λ represents the wavelength, d represents the number of bands, u represents a high the number of pixels of the spectral image, z 1 ,z 2 ,…,z u Corresponding to each pixel represents the elevation, Representation domain;

[0070] Computing for each pixel a normal, normal characteristics is obtained:

[0071] in, Represents normals x, y, z spatial coordinate axes projection;

[0072] Geometrical components obtained by calculation J: J = [J 1 , J 2 , ..., J u ] ú ;

[0073] in,

[0074]

[0075] c 1 , C 2 , C 3 , C 4 , ...

specific Embodiment approach 3

[0078] DETAILED Embodiment 3: Embodiment of the present embodiment of the second embodiment will be further described, the specific method for obtaining a partial matrix prior S2 of the computing comprises:

[0079] Traversing each pixel of the index k = 1,2, ..., u, the establishment of the dictionary D k = [H 1 , ..., h k-1 H k+1 , ..., h u I d ];

[0080] Among them, I d It represents a d-dimensional matrix;

[0081] H is calculated according to the formula k In the dictionary D k The sparse representation coefficient α:

[0082] MIN α ‖Α‖ 1 subject to h k = D k [alpha];

[0083] Local each element of matrix W priori W kj Assignment obtained by the following formula:

[0084]

[0085] W kj K represents an element row j-th column of W;

[0086] alpha j It represents the j-th column of the sparse representation coefficient, α j-1 It represents a coefficient represented by the sparse column j-1.

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a hyperspectral image eigen decomposition method based on digital surface model assistance, belongs to the technical field of hyperspectral image fusion processing, and aims to solve the problem of low precision of existing hyperspectral image eigendecomposition. The method comprises the following steps: inputting a hyperspectral image and digital surface model data, and calculating to obtain geometric components; calculating to obtain a local prior matrix; calculating to obtain a non-local prior matrix; and according to the geometric component, the local priori matrix and the non-local priori matrix, carrying out eigen decomposition, and outputting high spectral reflectivity and environment illumination. The invention is used for intrinsic decomposition of the hyperspectral image.

Description

Technical field [0001] The present invention relates to a high spectrum image intrinsic decomposition method, belonging to the technical field of high spectral image fusion processing. Background technique [0002] The high-spectral image has rich spectral information, but the high dimensional spectral space also causes high redundancy of information, which is not conducive to the processing interpretation of information. In order to better excavate information, various feature extraction has been designed, but these information extraction methods have essential defects. When the imaging conditions such as the ambient illumination change, the spectra obtained by the imaging will also change, which makes the spectrum have high uncertainty, which is reflected in the extraction of the characteristics of information. Unreliable. In order to solve this problem, it has great significance to study the intrinsic decomposition method based on the physical imaging model. The intrinsic deco...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): G06K9/62
CPCG06F18/2136G06F18/28
Inventor 谷延锋金旭东
Owner HARBIN INST OF TECH
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com