Model building and optimizing method for mass customization of two-dimension time-space correlation

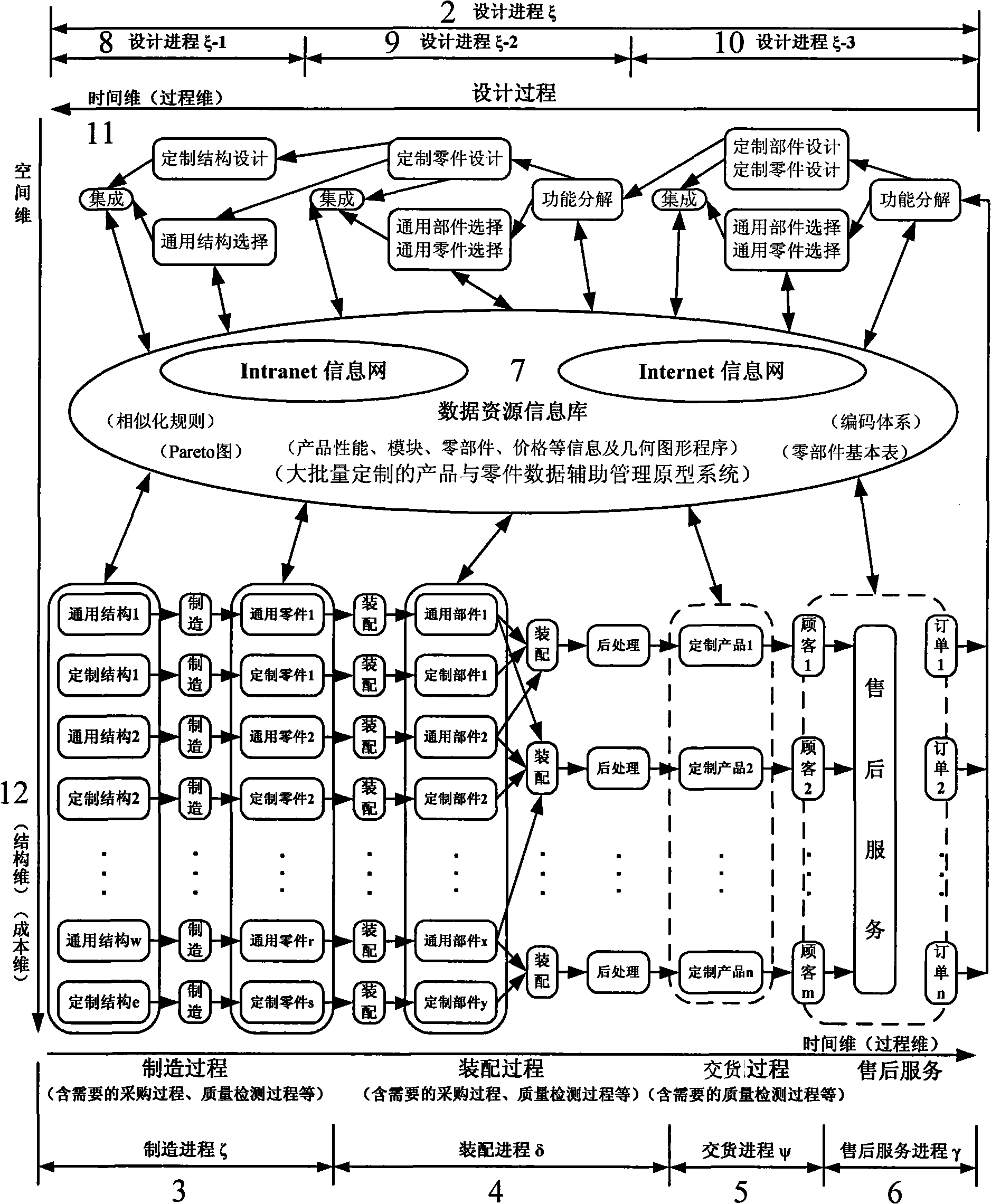
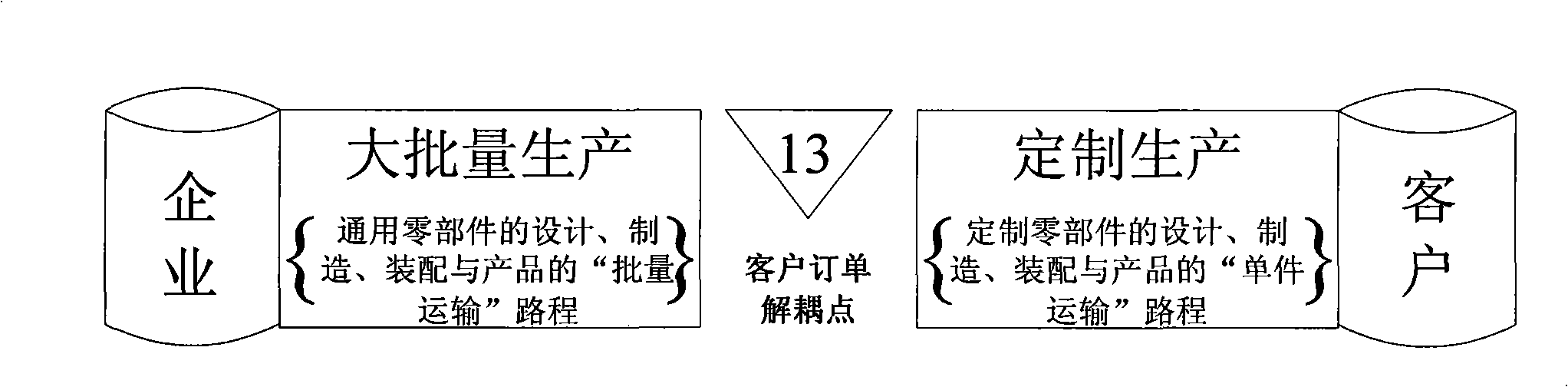
[0019] The present invention will be further explained below with reference to the drawings and examples.

[0020] A method for modeling and optimizing a two-dimensional space-time model for mass customization of the present invention includes modeling and optimization of a two-dimensional space-time model for mass customization, wherein:

[0021] 1) Mass customization of the two-dimensional space-time model modeling, using the time dimension described by the process model and the space dimension described by the product model, the total production time required for mass customization to complete the order is mapped to the time dimension, and the mass customization is used to complete the order The total cost of the required product is mapped to the spatial dimension;

[0022] 2) Mass customization of the two-dimensional space-time model optimization, complete the mathematical modeling of the mass-customization two-dimensional space-time model, and use heuristic optimization methods to solve the problem according to the mathematical model; the optimization of the time dimension is carried out for the operation process through product design , Manufacturing, assembly, delivery and after-sales service process, the best resource is rationally utilized, delaying the "time dimension customer order decoupling point"; the optimization of the space dimension is carried out for the product structure, by combining different products, components or parts The similarities in the part are merged and processed, so as to achieve the purpose of delaying the "spatial dimension customer order decoupling point".

[0023] Such as figure 1 As shown, the two-dimensional space-time model modeling of mass customization is a model of the total production time and total product cost required to complete an order through mass customization, including the time dimension 11 described by the process model and the spatial dimension 12 described by the product model ; Among them, the time dimension 11 describes the time course from the customer placing an order to the delivery of the customized product to the customer; the space dimension 12 can also be called the structural dimension or the cost dimension from a different perspective, and product quality and cost are carried out along this dimension The optimization of "Customer order decoupling point" 13 is achieved by merging the similarities in different products, components or parts.

[0024] Time dimension 11 and space dimension 12 use "process" as the "process model" to describe the entire customer order completion process, including a parent process-order process ζ1, and a data resource information database 7, through the Intranet information network and Internet information networks communicate with each other. Such as figure 2 As shown, the order process ζ1 includes five sub-processes, namely the design process ξ2, the manufacturing process ζ3, the assembly process δ4, the delivery process ψ5, and the after-sales service process γ6; the data resource information database 7 is in mass customized product and parts data Auxiliary management is built on the prototype system, including product performance, modules, parts, prices, and geometric graphics program information, as well as similarization rules, Pareto diagrams, coding systems, and basic parts table information.

[0025] Such as figure 2 As shown, the entire time span of the order process ζ1 describes the completion time of the order, which actually contains the so-called "product delivery date", which refers to the entire time from receiving the order to providing the customized product to the user Process, it has six states, namely the existence state, the execution state, the sleep state, the ready state, the pause state and the stop state:

[0026] 1) The order process ζ1 was born at the moment when the user order is received, and t is used here 0 Means that from t 0 After that, the order process is in a state of existence;

[0027] 2) The execution state of the order process ζ1 refers to the state in which one or more activities are in progress in the design process ξ2, the manufacturing process ζ3, the assembly process δ4, and the delivery process ψ5;

[0028] 3) The sleep state of the order process ζ1 refers to the state where all activities are forced to stop temporarily in the design process ξ2, the manufacturing process ζ3, the assembly process δ4, and the delivery process ψ5 due to the shortage of resources in the enterprise or other reasons, for example, After the order enters the delivery process ψ5, because there is no transportation tool immediately available, the assembled customer-specific product cannot be delivered to the customer immediately and is in a state of waiting for delivery;

[0029] 4) The ready state of the order process ζ1 refers to the state where none of the activities in the design process ξ2, the manufacturing process ζ3, the assembly process δ4, and the delivery process ψ5 are in progress, and all the required resources are ready, for example, a customized product is ready And the means of transport that delivered it to the customer, but it has not yet started "loading";

[0030] 5) The suspended state of the order process ζ1 means that none of the activities in the design process ξ2, the manufacturing process ζ3, the assembly process δ4, and the delivery process ψ5 are in progress, but the inspection or repair status of related equipment is being carried out;

[0031] 6) The stop state of the order process ζ1, refers to tend After the state, here, t end Indicates the moment when the customized product is delivered to the customer, such as the period of waiting for the customer to pay after the customized product is delivered to the customer. At this time, all activities related to the completion of the order by the company have been completed, and all the resources used have been "released" .

[0032] Mass customization two-dimensional spatiotemporal model optimization includes mass customization two-dimensional spatio-temporal mathematical model and heuristic optimization method flow; among which mass customization two-dimensional spatio-temporal mathematical model is about the total production time and products required to complete the order through mass customization The mathematical model of the total cost, the mathematical model of the order process ζ1 can be obtained by separately establishing the mathematical models of the design process ξ2, the manufacturing process ζ3, the assembly process δ4, the delivery process ψ5 and the after-sales service process γ6.

[0033] The main parameters of mass customization of the two-dimensional space-time mathematical model:

[0034] ●Use Г to indicate the total time taken by the company to complete the order as Г=t end -t 0;

[0035] ●Use Q to represent the N quality requirements of the order, q n (E.g. intensity q 1 , Stiffness q 2 , Material requirements q 3 Etc.), here, q 1 , Q 2 , Q 3 After normalization has been processed, the quality requirements in the customer order can be expressed as: Q = Σ j = 1 N q j ≥ Q 0 ;

[0036] ●Use G to represent the M functional requirements of the order, g n (E.g. g 1 , G 2 , G 3 Etc.), here, g 1 , G 2 , G 3 After normalization has been processed, the functional requirements in the customer order can be expressed as: G = Σ r = 1 M g r ≥ G 0 ;

[0037] ●t cstr Indicates the deadline for delivery requested by the customer;

[0038] 1) Two-dimensional space-time mathematical model of design process ξ(2):

[0039] The design process ξ is subdivided into design process ξ-18, design process ξ-29, and design process ξ-310:

[0040] ①For the design process ξ-18, the time, cost and influence coefficients related to the execution state, sleep state, ready state and pause state are: t j ξ-1 , C j ξ-1 , F j ξ-1 (t), f j ξ-1 (C)(j=1, 2, 3, 4);

[0041] ②For the design process ξ-2 9, the time, cost and influence coefficients related to the execution state, the sleep state, the ready state and the pause state respectively are: t k ξ-2 , C k ξ-2 , F k ξ-2 (t), f k ξ-2 (C)(k=1, 2, 3, 4);

[0042] ③For the design process ξ-3 10, the time, cost and influence coefficients related to the execution state, the sleep state, the ready state and the pause state respectively are: t l ξ-3 , C l ξ-3 , F l ξ-3 (t), f l ξ-3 (C) (l=1, 2, 3, 4);

[0043] Then get the mathematical model related to product design:

[0044] min Σ m = 1 3 Σ n = 1 4 f n ξ - m ( t ) × t n ξ - m - - - ( 1 - 1 )

[0045] min Σ m = 1 3 Σ n = 1 4 f n ξ - m ( C ) × C n ξ - m - - - ( 1 - 2 )

[0046] s . t . Σ m = 1 3 Σ n = 1 4 f n ξ - m ( t ) × t n ξ - m t cstmr - t 0 - - - ( 1 - 3 )

[0047] Σ j = 1 N q j ≥ Q 0 - - - ( 1 - 4 )

[0048] Σ k = 1 M g k ≥ G 0 - - - ( 1 - 5 )

[0049] F in the above formula n ξ-m (t), f n ξ-m (C) (n = 1, 2, 3, 4), for mass production, they are always equal to 1; for custom production, they are greater than 1; and for mass customization, the goal is to equal 1 Or less than 1 (this is usually obtained by improving the existing mass customization operations, etc.);

[0050] In addition, from the perspective of space dimensions, another form of mathematical model is established, namely:

[0051] ①For the design process ξ-18, the time and cost required for custom structure design and general structure design and their influence coefficients due to customer customization are: t cust ξ-1 , F cust ξ-1 (t), C cust ξ-1 , F cust ξ-1 (C), t com ξ-1 , F com ξ-1 (t), C com ξ-1 , F com ξ-1 (C);

[0052] ②For the design process ξ-2 9, the time and cost required for custom part design, general part selection and their influence coefficients due to customer customization are: t cust ξ-2 , F cust ξ-2 (t), C cust ξ-2 , F cust ξ-2 (C), t com ξ-2 , F com ξ-2 (t), C com ξ-2 , F com ξ-2 (C);

[0053] ③For the design process ξ-3 10, the time and cost required for custom component design, general component selection and their coefficients affected by customer customization are: t cust ξ-3 , F cust ξ-3 (t), C cust ξ-3 , F cust ξ-3 (C), t com ξ-3 , F com ξ-3 (t), C com ξ-3 , F com ξ-3 (C);

[0054] Thus, a mathematical model related to product design is obtained:

[0055] min Σ m = 1 3 [ f cust ξ - m ( t ) × t cust ξ - m + f com ξ - m ( t ) × t com ξ - m ] - - - ( 1 - 6 )

[0056] min Σ n = 1 3 [ f cust ξ - n ( C ) × C cust ξ - n + f com ξ - n ( C ) × C com ξ - n ] - - - ( 1 - 7 )

[0057] s . t . Σ m = 1 3 [ f cust ξ - m ( t ) × t cust ξ - m + t com ξ - m ( t ) × t com ξ - m ] t cstmr - t 0 - - - ( 1 - 8 )

[0058] Σ j = 1 N q i ≥ Q 0 - - - ( 1 - 9 )

[0059] Σ k = 1 M g k ≥ G 0 - - - ( 1 - 10 )

[0060] Obviously, generally speaking f cust ξ-p (t), f cust ξ-p (C) (p=1, 2, 3) is greater than 1, and f com ξ-p (t), f com ξ-p (C) (p = 1, 2, 3) is equal to 1; for this reason, the goal of mass customization is to delay the "customer order decoupling point" by converting the customized product design part into a common part design as much as possible. , And then improve the existing mass production design process and resource allocation to make these coefficients less than 1;

[0061] 2) Two-dimensional space-time mathematical model of manufacturing process ζ3

[0062] ① The manufacturing process ζ3 is born at the moment when the manufacturing department receives the processing operation request, it is in a state of existence;

[0063] ② The execution state of the manufacturing process ζ3 refers to the state where one or more general structures or customized structures are being processed. Here, use t 1 ζ , C 1 ζ Respectively represent the sum of all the time and the sum of all costs spent in the manufacturing process ζ in this state, and f 1 ζ (t), f 1 ζ (C) respectively indicate the 1 ζ , C 1 ζ The influence coefficient;

[0064] ③The sleep state of the manufacturing process ζ3, such as the preparation of various processing tools or raw materials during processing. This is the main production preparation stage to be eliminated in mass customization. Here, use t 2 ζ , C 2 ζ Respectively represent the sum of all the time and the sum of all costs spent in the manufacturing process ζ in this state, and f 2 ζ (t), f 2 ζ (C) respectively indicate the 2 ζ , C 2 ζ The influence coefficient;

[0065] ④The ready state of the manufacturing process ζ3 refers to the state in which the processing department has arranged the processing operation plan and prepared various resources required for processing. This state is the rate of resource waste caused by idle equipment, personnel, etc. Almost the highest; it is a state that enterprises should absolutely and can eliminate; here, use t 3 ζ , C 3 ζ Respectively represent the sum of all the time and the sum of all costs spent in the manufacturing process ζ in this state, and f 3ζ (t), f 3 ζ (C) Respectively indicate customer customization 3 ζ , C 3 ζ The influence coefficient;

[0066] ⑤The pause state of the manufacturing process ζ3 refers to a state in which the production process is temporarily stopped due to the needs of inspection, supervision or equipment repair during the manufacturing process; this is a state that is usually encountered, similar to the ready state, It is also a state where the resource waste rate is very high due to idle equipment, personnel, etc.; here, use t 4 ζ , C 4 ζ Respectively represent the sum of all the time and all the costs spent in the manufacturing process ζ in this state, and f 4 ζ (t), f 4 ζ (C) Respectively indicate customer customization 4 ζ , C 4 ζ The influence coefficient;

[0067] ⑥ The stop state of the manufacturing process ζ3 means that all processing operations of the customized product are completed and all resources are released;

[0068] Thus, a mathematical model related to product manufacturing is obtained:

[0069] min Σ n = 1 4 f n ζ ( t ) × t n ζ - - - ( 2 - 1 )

[0070] min Σ n = 1 4 f n ζ ( C ) × C n ζ - - - ( 2 - 2 )

[0071] s . t . Σ n = 1 4 f n ζ ( t ) × t n ζ t cstmr - t 0 - - - ( 2 - 3 )

[0072] Σ j = 1 N q j ≥ Q 0 - - - ( 2 - 4 )

[0073] Σ k = 1 M g k ≥ G 0 - - - ( 2 - 5 )

[0074] F in the above formula n ζ (t), f n ζ (C) (n = 1, 2, 3, 4), for mass production, they are always equal to 1; for custom production, they are greater than 1; and for mass customization, the goal is to make them less than or Equal to 1

[0075] In addition, from the perspective of space dimensions, another form of mathematical model can be established, namely:

[0076] Suppose the time and cost required for general parts and customized parts in the manufacturing process ζ3 and their influence coefficients affected by customer customization are respectively: t cust ζ , F cust ζ (t), C cust ζ , F cust ζ (C), t com ζ , F com ζ (t), C com ζ , F com ζ (C);

[0077] Thus, a mathematical model related to product manufacturing is obtained:

[0078] min f cust ζ ( t ) × t cust ζ + f com ζ ( t ) × t com ζ - - - ( 2 - 6 )

[0079] min f cust ζ ( C ) × C cust ζ + f com ζ ( C ) × C com ζ - n - - - ( 2 - 7 )

[0080] s . t . f cust ζ ( t ) × t cust ζ + f com ζ ( t ) × t com ζ t cstmr - t 0 - - - ( 2 - 8 )

[0081] Σ j = 1 N q j ≥ Q 0 - - - ( 2 - 9 )

[0082] Σ k = 1 M g k ≥ G 0 - - - ( 2 - 10 )

[0083] Obviously, f cust ζ (t), f cust ζ (C) is greater than 1, and f com ζ (t), f com ζ (C) is equal to 1. Therefore, the goal of mass customization is to delay the "customer order decoupling point"13 by converting customized parts into general parts as much as possible, and then by improving the existing mass production manufacturing process and resource allocation, etc. Make these coefficients less than 1;

[0084] 3) Two-dimensional space-time mathematical model of assembly process δ4

[0085] According to the previous definition of process, suppose t 1 δ , C 1 δ Respectively represent the sum of all the time and all the costs spent in the assembly process δ4 in its execution state, and f 1 δ (t), f 1 δ (C) Respectively indicate customer customization 1 δ , C 1 δ The influence coefficient; suppose t 2 δ , C 2 δ Respectively represent the sum of all the time and the sum of all costs in the assembly process δ4 in its sleep state (for example, the assembly department is forced to stop assembly activities because it cannot obtain the required parts or assembly tools immediately), and f 2 δ (t), f 2 δ (C) Respectively indicate customer customization 2 δ , C 2 δ The influence coefficient; suppose t 3 δ , C 3 δ Respectively represent the sum of all the time and all the costs spent in the assembly process δ4 in its ready state, and f 3 δ (t), f 3 δ (C) Respectively indicate customer customization 3 δ , C 3 δ The influence coefficient; suppose t 4 δ , C 4 δ Respectively represent the sum of all time and the sum of all costs in the assembly process δ4 in its suspended state (such as temporarily stopping assembly activities to ensure assembly quality, etc. for inspection, supervision or repair, etc.), and f 4 δ (t), f 4 δ (C) Respectively indicate customer customization 4 δ , C 4 δ The influence coefficient;

[0086] Thus, a mathematical model related to product assembly is obtained:

[0087] min Σ n = 1 4 f n δ ( t ) × t n δ - - - ( 3 - 1 )

[0088] min Σ n = 1 4 f n δ ( C ) × C n δ - - - ( 3 - 2 )

[0089] s . t . Σ n = 1 4 f n δ ( t ) × t n δ t cstmr - t 0 - - - ( 3 - 3 )

[0090] F in the above formula n δ (t), f n δ (C) (n = 1, 2, 3, 4), for mass production, they are always equal to 1; for custom production, they are greater than 1; and for mass customization, the goal is to make them less than or Equal to 1

[0091] In addition, from the perspective of space dimensions, another form of mathematical model is established, namely

[0092] Suppose the time and cost required for general parts and customized parts in the assembly process δ4 and their coefficients affected by customer customization are respectively: t cust δ , F cust δ (t), C cust δ , F cust δ (C), t com δ , F com δ (t), C com δ , F com δ (C).

[0093] Thus, a mathematical model related to product assembly is obtained:

[0094] min f cust δ ( t ) × t cust δ + f com δ ( t ) × t com δ - - - ( 3 - 4 )

[0095] min f cust δ ( C ) × C cust δ + f com δ ( C ) × C com δ - - - ( 3 - 5 )

[0096] s . t . f cust δ ( t ) × t cust δ + f com δ ( t ) × t com δ t cstmr - t 0 - - - ( 3 - 6 )

[0097] Obviously, f cust δ (t), f cust δ (C) is greater than 1, and f com δ (t), f com δ (C) is equal to 1; therefore, the goal of mass customization is to delay the "customer order decoupling point" 13 through generalization, and then improve the existing mass production assembly process and resource allocation to make these parameters less than 1;

[0098] 4) Two-dimensional space-time mathematical model of delivery process ψ5

[0099] Let t 1 ψ , C 1 ψ Respectively represent the sum of all the time and all the costs spent in the delivery process ψ5 in its execution state, and f 1 ψ (t), f 1 ψ (C) Respectively indicate customer customization 1 ψ , C 1 ψ The influence coefficient; suppose t 2 ψ , C 2 ψ Respectively represent the sum of all the time and the sum of all costs in the delivery process ψ5 in its sleep state (for example, due to waiting for certain procedures or required tools during the delivery process, the delivery activities are temporarily terminated), While f 2 ψ (t), f 2 ψ (C) Respectively indicate customer customization 2 ψ , C 2 ψThe influence coefficient; suppose t 3 ψ , C 3 ψ Respectively represent the sum of all the time and all the costs spent in the delivery process ψ5 in its ready state, and f 3 ψ (t), f 3 ψ (C) Respectively indicate customer customization 3 ψ , C 3 ψ The influence coefficient; suppose t 4 ψ , C 4 ψ Respectively represent the sum of all the time and the sum of all the costs spent in the delivery process ψ5 in its suspended state (such as for verification of delivery procedures, etc.), and f 4 ψ (t), f 4 ψ (C) Respectively indicate customer customization 4 ψ , C 4 ψ The influence coefficient;

[0100] Thus, a mathematical model related to product delivery is obtained:

[0101] min Σ n = 1 4 f n ψ ( t ) × t n ψ - - - ( 4 - 1 )

[0102] min Σ n = 1 4 f n ψ ( C ) × C n ψ - - - ( 4 - 2 )

[0103] s . t . Σ n = 1 4 f n ψ ( t ) × t n ψ t cstmr - t 0 - - - ( 4 - 3 )

[0104] F in the above formula n ψ (t), f n ψ (C) For mass production, they are always equal to 1; for custom production, they are greater than 1, because mass production uses mass transportation, etc., to spread the transportation cost and so on to each product; mass production The goal of customization is to strive for delivery costs equal to or less than mass production by improving the transportation process and/or resources;

[0105] In addition, from the perspective of space dimensions, another form of mathematical model is established, that is, from the perspective of supply chain, the batch of customized or non-customized products that are shipped at the same time as the customized product is set to i, where and The number of customized or non-customized products with the same or intersecting parts of the transportation route of the customized product is j, assuming

[0106] ①The total average transportation cost per unit distance of these customized products (including the customized product, and set the customized product number as j+1) is u q (q=1, 2,..., j+1), obviously usually u q It is a monotonic, non-increasing function with the number of products transported each time.

[0107] ②The unit time penalty factor for these customized products not being shipped to the destination on time (early or late) is the advance coefficient γ q , Tardiness Coefficient τ q (q=1, 2,..., j+1); The size or sign of the penalty factor is determined by both parties. Obviously, the size and sign of the penalty factor actually reflect the customer’s satisfaction ρ q (q=1, 2,..., j+1), here, suppose that the penalty factor term is equal to the product price p q Multiplied by the penalty factor ε q , Here, q=1, 2,..., j+1, and p q The smaller the value, the more satisfied the customer; therefore, there is ρ q =ε q ×p q ,among them

[0108] ③The transportation distances of these customized products are respectively L q , The total average transportation speed is v.

[0109] ④The delivery time of these customized products is t be , The time of delivery is respectively t q end (q=1, 2,..., j+1).

[0110] Therefore, the mathematical model related to product delivery is:

[0111] min Σ q = 1 j + 1 ( t q end - t be ) - - - ( 4 - 5 )

[0112] min Σ q = 1 j + 1 [ L q × u q + ϵ q × p q × ( t q end - t be ) ] - - - ( 4 - 6 )

[0113] s . t . t j + 1 end - t be t cstmr - t 0 - - - ( 4 - 7 )

[0114] 5) Two-dimensional spatio-temporal mathematical model of after-sales service process γ6

[0115] According to the previous definition of "process", suppose t 1 γ , C 1 γ Respectively represent the sum of all the time and all the costs spent in the after-sales service process γ6 in its execution state, and f 1 γ (t), f 1 γ (C) Respectively indicate customer customization 1 γ , C 1 γ The influence coefficient; suppose t 2 γ , C 2 γ Respectively indicate the sum of all the time and the sum of all the costs that the after-sales service process γ6 is in its sleep state (for example, due to waiting for the required tools or parts, etc., forced to temporarily terminate after-sales service activities) 2 γ (t), f 2 γ (C) Respectively indicate customer customization 2 γ , C 2 γ The influence coefficient; suppose t 3 γ , C 3 γ Respectively represent the sum of all the time that the after-sales service process γ6 is in its ready state and the sum of all the costs, and f 3 γ (t), f 3 γ (C) Respectively indicate customer customization 3 γ , C 3 γ The influence coefficient; suppose t 4 γ , C 4 γ Respectively indicate that the after-sales service process γ6 is in its suspended state (for example, in the process of after-sales service activities, discuss with the customer about the collection of handling fees or where the required parts, tools, etc., are obtained or purchased, etc.), the sum of all time and all costs The sum of costs, and f 4 γ (t), f 4 γ (C) Respectively indicate customer customization 4 γ , C 4 γ The coefficient of influence.

[0116] Thus, a mathematical model related to product delivery is obtained:

[0117] min Σ k = 1 4 f k γ ( t ) × t k γ - - - ( 5 - 1 )

[0118] min Σ k = 1 4 f k γ ( C ) × C k γ - - - ( 5 - 2 )

[0119] s . t . Σ j = 1 N q j ≥ Q 0 - - - ( 5 - 3 )

[0120] Σ k = 1 M g k ≤ G 0 - - - ( 5 - 4 )

[0121] Obviously, in the after-sales service process, the main factors that affect the cost are: ①the price of the required parts; ②the difficulty of obtaining the required parts; ③the workload of the required service personnel; Whether the tools to be used are valuable or not, and whether the tools are easy to obtain; ⑤whether the technical content required for after-sales service is high; ⑥the location of after-sales service is close to the company's after-sales service department;

[0122] Therefore, from the perspective of space dimension, another form of mathematical model is established, namely

[0123] Suppose the time and cost related to the required general parts and/or tools, customized parts and/or tools, etc. in the after-sales service process γ6, and their coefficients affected by customer customization are: t cust γ , F cust γ (t), C cust γ , F cust γ (C), t com δ , F com δ (t), C com γ , F com γ (C), the mathematical model related to after-sales service is obtained:

[0124] min f cust γ ( t ) × t cust γ + f com γ ( t ) × t com γ - - - ( 5 - 5 )

[0125] min f cust γ ( C ) × C cust γ + f com γ ( C ) × C com γ - - - ( 5 - 6 )

[0126] s . t . Σ j = 1 N q j ≥ Q 0 - - - ( 5 - 7 )

[0127] Σ k = 1 M g k ≥ G 0 - - - ( 5 - 8 )

[0128] Obviously, f cust δ (t), f cust δ (C) is greater than 1, and f com δ (t), f com δ (C) equal to 1, the goal of mass customization is to make these coefficients less than or equal to 1 by improving after-sales service programs or resource preparation;

[0129] 6) Mass customization of two-dimensional spatio-temporal mathematical model

[0130] According to the above discussion, the following two mathematical models based on the two-dimensional space-time model are obtained, namely

[0131] ③The time-dimensional mathematical model based on the design process ξ2, the manufacturing process ζ3, the assembly process δ4, the delivery process ψ5 and the after-sales service process γ6:

[0132] min Σ m = 1 3 Σ n = 1 4 f n ξ - m ( t ) × t n ξ - m + Σ n = 1 4 [ f n ζ ( t ) × t n ζ + f n δ ( t ) × t n δ + f n ψ ( t ) × t n ψ + f n γ ( t ) × t n γ ] - - - ( 6 - 1 )

[0133] min Σ m = 1 3 Σ n = 1 4 f n ξ - m ( C ) × C n ξ - m + Σ n = 1 4 [ f n ζ ( C ) × C n ζ + f n δ ( C ) × C n δ - - - ( 6 - 2 )

[0134] f n ψ ( C ) × C n ψ + f n γ ( C ) × C n γ ]

[0135] s . t . Σ m = 1 3 Σ n = 1 4 f n ξ - m ( t ) × t n ξ - m + Σ n = 1 4 [ f n ζ ( t ) × t n ζ + f n δ ( t ) × t n δ + f n ψ ( t ) × t n ψ ] t cstmr - t 0 - - - ( 6 - 3 )

[0136] Σ j = 1 N q j ≥ Q 0 - - - ( 6 - 4 )

[0137] Σ k = 1 M g k ≥ G 0 - - - ( 6 - 5 )

[0138] ④The spatial dimension mathematical model based on the design process ξ2, the manufacturing process ζ3, the assembly process δ4, the delivery process ψ5 and the after-sales service process γ6:

[0139] min Σ m = 1 3 [ f cust ξ - m ( t ) × t cust ξ - m + f com ξ - m ( t ) × t com ξ - m ] + f cust ζ ( t ) × t cust ζ + f com ζ ( t ) × t com ζ +

[0140] f cust δ ( t ) × t cust δ + f com δ ( t ) × t com δ + Σ q = 1 j + 1 ( t q end - t be ) + f cust γ ( t ) × t cust γ + f com γ ( t ) × t com γ - - - ( 6 - 6 )

[0141] min Σ n = 1 3 [ f cust ξ - n ( C ) × C cust ξ - n + f com ξ - n ( C ) × C com ξ - n ] + f cust ζ ( C ) × C cust ζ

[0142] + f com ζ ( C ) × C com ζ - n + f cust δ ( C ) × C cust δ + f com δ ( C ) × C com δ

[0143] + f cust γ ( C ) × C cust γ + f com γ ( C ) × C com γ

[0144] + Σ q = 1 j + 1 [ ( L q × u q + ϵ q × p q × ( t q end - t be ) ] - - - ( 6 - 7 )

[0145] s . t . Σ m = 1 3 [ f cust ξ - m ( t ) × t cust ξ - m + f com ξ - m ( t ) × t com ξ - m ] + f cust ζ ( t ) × t cust ζ + f com ζ ( t ) × t com ζ

[0146] + f cust δ ( t ) × t cust δ + f com δ ( t ) × t com δ + t j + 1 end - t be t cstmr - t 0 - - - ( 6 - 8 )

[0147] Σ j = 1 N q j ≥ Q 0 - - - ( 6 - 9 )

[0148] Σ k = 1 M g k ≥ G 0 - - - ( 6 - 10 )

[0149] 7) Mathematical model of "customer order decoupling point" 13 based on spatial dimension

[0150] According to the spatial dimension mathematical model based on the design process ξ2, the manufacturing process ζ3, the assembly process δ4, the delivery process ψ5, and the after-sales service process γ6, it can be known that the common transportation path between common parts and different products can be used to solve the "customer order "Coupling point" 13 is described, that is, for the above-mentioned customized products, the "customer order decoupling point" 13 should be moved backward as much as possible during the implementation of mass customization, that is, the "customer order decoupling point" 13 should be moved to the " Movement in the direction of mass production, expressed by a mathematical model as

[0151] min Σ m = 1 3 f cust ξ - m ( t ) × t cust ξ - m + f cust ζ ( t ) × t cust ζ × f cust δ ( t ) × t cust δ + f cust γ ( t ) × t cust γ + f cust ψ ( t ) × t cust ψ - - - ( 7 - 1 )

[0152] min Σ n = 1 3 f cust ξ - n ( C ) × C cust ξ - n + f cust ζ ( C ) × C cust ζ + f cust δ ( C ) × C cust δ - - - ( 7 - 2 )

[0153] + f cust γ ( C ) × C cust γ + f cust ψ ( c ) × C cust ψ

[0154] s . t . Σ m = 1 3 [ f cust ξ - m ( t ) × t cust ξ - m + f com ξ - m ( t ) × t com ξ - m ] + f cust ζ ( t ) × t cust ζ + f com ζ ( t ) × t com ζ - - - ( 7 - 3 )

[0155] + f cust δ ( t ) × t cust δ + f com δ ( t ) × t com δ + t j + 1 end - t be t cstmr - t 0

[0156] Σ j = 1 N q j ≥ Q 0 - - - ( 7 - 4 )

[0157] Σ k = 1 M g k ≥ G 0 - - - ( 7 - 5 )

[0158] Here, t cust ψ , F cust ψ (t), C cust ψ , F cust ψ (C) Respectively represent the corresponding time and cost of all the distances in the delivery process of customized products that are different from mass-produced products and the coefficient of the size of the impact of customer customization; in order to reduce the total cost of customized products (in equation (7-2)) The key to moving back the "customer order decoupling point" 13 is to take various measures to reduce the delivery time (the sum of the items in formula (7-1)) (7-2) and the influence coefficients of formula (7-1), such as: ① realize flexible operation, and the parts must be universal; ② the geometry of the fixture must be universal, so that many parts with different shapes are used Positioning in the same way; ③Design features must be universal to ensure the use of the same processing tools; ④Materials must be universal to avoid stopping production due to replacement of materials; ⑤Delivery channels are universal to avoid the entire delivery of customized products There are separate journeys in the cargo process.

[0159] Reference Figure 4 , As the flow chart of the heuristic optimization method, based on the mass-customized two-dimensional spatio-temporal mathematical model; the heuristic optimization method is an optimization method that gradually approximates and merges the satisfactory solution to reduce the solution space; below, the above based on the spatial dimension Take the mathematical model of as an example to illustrate the process of the optimization method:

[0160] Suppose there are a total of J orders to be processed. Here, for the convenience of explaining the problem, a multifunctional group Ω is assigned to each order i i (In a specific enterprise, a multi-functional project team may undertake multiple order tasks at the same time, that is, Ω here i It may be the same) (i=1, 2,..., J), the same steps and tools are used in the processing of each order (such as the same cost "tracking" software, time "tracking" software, and optimization method software Wait). Therefore, the heuristic optimization method is gradually explained as follows, namely:

[0161] Step one, process order i. Assign the order to the multifunctional team Ω i , And establish the processing time and cost tracking project of the order (that is, create a new project in the database management system) At the same time, create order constraints (such as the delivery date, quality, function and other requirements specified in the order);

[0162] For example, suppose the lower limit and upper limit of the interval of the quality (such as wear resistance index, etc.) (Q) required by the customer are Q respectively min , Q max , Then: Q min ≤Q r ≤Q max;Functions required by customers (such as power size) (F r ) The lower and upper limits of the interval are respectively F min , F max , Then: F min ≤F r ≤F max. Then, adopt a standardized method, for example, for quality requirements: u Qmin ≤u Qr ≤u Qmax , Where u Qmin = 1, u Qr = Q r Q min , u Q max = Q max Q min ; Similarly, the functional requirements are: u Fmin ≤u Fr ≤u Fmax , Where u Fmin = 1, u Fr = F r F min , u F max = F max F min . Therefore, assuming that the results obtained after similar processing according to the various quality requirements given by the customer are (j=1, 2,..., N), there are constraints: Σ j = 1 N u Qj ≥ Q 0 ; Similarly, suppose that the results obtained after similar processing of the various functional requirements given by the customer are respectively (r=1, 2,..., M), there are constraints: Σ r = 1 M u Fr ≥ G 0 ; Among them, Q 0 , G 0 See the meaning above;

[0163] In addition, let t cstr Indicates the deadline for delivery requested by the customer. The total time taken by the company to complete the order is t end -t 0 , So the constraint on the delivery date is: t end -t 0 cstr -t 0; Where t end , T 0 See the meaning above;

[0164] Step two, in Create sub-projects of design process ξ (further divided into three sub-processes below), manufacturing process ζ, assembly process δ, delivery process ψ and after-sales service process γ;

[0165] Step three, through the design sub-process ξ-3, obtain various general parts and parts that need to be customized; then, query the product (including parts) information database (product performance, modules, parts, prices, etc.) Geometric structure graphics, etc.), and enter the selected general parts and custom parts to be designed in terms of production time and cost data;

[0166] For example, suppose the execution state (j=1), sleep state (j=2), ready state (j=3) and pause state (j=4) of this process correspond to the total time and cost respectively: (t j ξ-3 , C j ξ-3 , F j ξ-3 (t), f j ξ-3 (C)) (j = 1, 2, 3, 4), then the total time corresponding to this process (T tt3 ) And cost (C tt3 ) Are: T tt 3 = Σ j = 1 4 f j ξ - 3 ( t ) × t j ξ - 3 , C tt 3 = Σ j = 1 4 f j ξ - 3 ( C ) × C j ξ - 3 ;

[0167] Step four, through the design sub-process ξ-2, and further based on functional decomposition, the custom parts to be designed are divided into two types that need to be customized and can be directly selected from the product (including parts) information database after generalization. Data entry related to production time and product cost, namely t k ξ-2 , C k ξ-2 , F k ξ-2 (t), f k ξ-2 (C)(k=1, 2, 3, 4);

[0168] Similar to "Step 3", we can see that the total time (T tt2 ) And cost (C tt2 ) Are: T tt 2 = Σ k = 1 4 f k ξ - 3 ( t ) × t k ξ - 3 , C tt 2 = Σ k = 1 4 f k ξ - 3 ( C ) × C k ξ - 3 ;

[0169] Step 5, through the design sub-process ξ-1, complete the design of the custom parts and the selection of the general structure, and enter the relevant production time and product cost data of the custom structure design and the general structure selection, namely t l ξ-1 , C l ξ-1 , F l ξ-1 (t), f l ξ-1 (C) (l=1, 2, 3, 4);

[0170] Similar to "Step 3", we can see that the total time (T tt1 ) And cost (C tt1 ) Are: T tt 1 = Σ l = 1 4 f l ξ - 3 ( t ) × t l ξ - 3 , C tt 1 = Σ l = 1 4 f l ξ - 3 ( C ) × C l ξ - 3 ;

[0171] Step six, call the mathematical model (formulas (1-1), (1-2), (1-3), (1-4), (1-5)) to obtain the data in steps three, four, and five Is the solution satisfactory? Does it meet the constraint requirements? If yes, use the data in steps 3, 4, and 5 as the initial point to obtain the feasible region space Θ of the model 1; Otherwise, go to step 3, repeat "step 3" ~ "step 5" and re-determine the relevant data;

[0172] Obviously, the feasible domain space of the model at this time Θ 1 , Has not considered the problems such as equipment failure or resource shortage that may be encountered in the manufacturing and assembly stages, so it can be considered that it is still an "unconstrained" optimization solution relative to the manufacturing and assembly stages;

[0173] Step seven, open the sub-project of the manufacturing process ζ, inherit all the data related to the process in steps three, four, and five, and then divide all tasks belonging to the process into two categories: general parts and customized parts. Suppose the time and cost required for general parts and customized parts in this process and their influence coefficients of customer customization are respectively: t cust ζ , F cust ζ (t), Ccust ζ , F cust ζ (C), t com ζ , F com ζ (t), C com ζ , F com ζ (C), call the mathematical model (formulas (2-1), (2-2), (2-3), (2-4), (2-5)), whether the steps three, four, five and in Are you satisfied with the optimized solution obtained in this process? Does it meet the constraints? If yes, use the above data as the initial point to obtain the feasible region space Θ of the model 2; Otherwise, go to step 3. Obviously, Θ 2 ⊆ Θ 1 ;

[0174] Feasible region space Θ 2 Relative to the feasible region space Θ 1 In other words, due to the increased considerations, such as the requirements for manufacturing equipment in the manufacturing process, there are usually: Θ 2 ⋐ Θ 1 Yes, it means that the solution space is reduced;

[0175] Step 8, open the sub-project of the assembly process δ, inherit all the data related to the process in each of the above steps, and then divide the various parts to be assembled into two categories: customized and general. Similar to "Step Seven", confirm t cust δ , F cust δ (t), C cust δ , F cust δ (C), t com δ , F com δ (t), C com δ , F com δ (C), and call the mathematical model (Equations (3-1), (3-2), (3-3)), are you satisfied with the previous steps and the optimized solution obtained in this process? Does it meet the constraints? If yes, use the above data as the initial point to obtain the feasible region space Θ of the model 3; Otherwise, if you are not satisfied with the data inherited in the design process ξ, go to step 3; if you are not satisfied with the data inherited in the manufacturing process ζ, go to step 7; obviously, Θ 3 ⊆ Θ 2 ⊆ Θ 1 ;

[0176] Feasible region space Θ 3 Relative to the feasible region space Θ 2 In other words, due to the increased considerations, such as the requirements for parts and assembly equipment in the assembly process, there are usually: Θ 3 ⋐ Θ 2 Yes, it means that the solution space is reduced;

[0177] Step 9: Open the delivery process ψ sub-project, inherit the data in the above steps, and query all customer orders within the enterprise;

[0178] First, determine u according to order i (see step 1), constraints, etc. q , Ε q , L q , V, t be , T q end , Q. Then, call the mathematical model (formulas (4-5), (4-6), (4-7)). Are you satisfied with the data obtained in the previous steps and the optimized solution of this process? Does it satisfy the constraints? If yes, use the above data as the initial point to obtain the feasible region space Θ of the model 4; Otherwise, if you are not satisfied with the data inherited in the design process ξ, go to step 3; if you are not satisfied with the data inherited in the manufacturing process ζ, go to step 7; if it is in the assembly process δ If the inherited data is not satisfactory, go to step 8. Obviously, Θ 4 ⊆ Θ 3 ⊆ Θ 2 ⊆ Θ 1 ;

[0179] Similar to the previous analysis, we can see that the feasible region space Θ 4 Relative to the feasible region space Θ 3 In other words, due to the increased considerations, such as the requirements for parts and assembly equipment in the assembly process, there are usually: Θ 4 ⋐ Θ 3 Yes, it means that the solution space is reduced;

[0180] Step 10, open the after-sales service process γ sub-item, inherit the data in the above steps, and then query all customer orders within the enterprise, and determine t according to the order i (see step 1) constraints, etc. cust γ , F cust γ (t), C cust γ , F cust γ (C), t com γ , F com γ (t), C com γ , F com γ (C), call the mathematical model (formulas (5-5), (5-6), (5-7), (5-8)), are you satisfied with the previous steps and the optimized solution obtained in this process? Does it meet the constraints? If yes, take all the existing data as the initial point to obtain the feasible region space Θ of the model 5 , And obtain a satisfactory solution in the feasible region space, then go to step 11; otherwise, if it is not satisfied with the data inherited in the design process ξ, go to step 3; if it is in the manufacturing process ζ If the inherited data is not satisfied, go to step 7; if you are not satisfied with the data in the assembly process, go to step 8; if you are not satisfied with the data in the delivery process ψ, go to step 9. Obviously, Θ 5 ⊆ Θ 4 ⊆ Θ 3 ⊆ Θ 2 ⊆ Θ 1 ;

[0181] Similar to the previous analysis, we can see that the feasible region space Θ 5 Relative to the feasible region space Θ 4 In terms of increased considerations, such as user satisfaction, etc., there are usually: Θ 5 ⋐ Θ 4 Yes, it means that the solution space is reduced;

[0182] Step eleven, the order i is processed, and it is judged whether i is equal to J. If i=J, go to step twelve; otherwise, let i=i+1, go to step 1, process the order (i+1).

[0183] Step twelve, end.

[0184] So far, it can be seen that in the gradual processing of orders, as the feasible domain space is gradually reduced, the optimized solution obtained in the subsequent steps is gradually approaching the "real situation", which is a process of "gradual refinement" .

[0185] Such as figure 1 As shown, the two-dimensional space-time model for mass customization is a model of the total production time and total product cost required to complete an order through mass customization, including the time dimension 11 described by the process model and the space dimension 12 described by the product model; Among them, the time dimension 11 and the space dimension 12 use "process" as the "process model" to describe the entire customer order completion process, including a parent process-order process ζ1 and a data resource information database 7, through the Intranet information network and Internet information networks communicate with each other. Such as figure 2 As shown, the order process ζ1 includes five sub-processes, namely the design process ξ2, the manufacturing process ζ3, the assembly process δ4, the delivery process ψ5, and the after-sales service process γ6; the data resource information database 7 is in mass customized product and parts data Auxiliary management is built on the prototype system, including product performance, modules, parts, prices and geometric graphics program information, as well as similarization rules, Pareto diagrams, coding systems and basic parts table information;

[0186] The entire time span of the order process ζ1 describes the completion time of the order. It actually contains the so-called "product delivery date", which refers to the entire process from receiving an order to providing customized products to users. There are six states, namely existence state, execution state, sleep state, ready state, pause state and stop state;

[0187] In the process of fulfilling customer orders, the overall optimization of time, quality and cost is carried out through time dimension and space dimension. Combine the above pairs figure 1 The description of "process" in figure 1 "Time dimension" and "space dimension" give some explanations:

[0188] ●Time dimension. The time dimension describes the time history from the customer placing an order to the delivery of the customized product to the customer. This is generally described by the process model, so it is also called the process dimension. For example, the optimization of the product delivery date is a typical process along the "time dimension". example.

[0189] The key to MC optimization in time dimension is to effectively delay the "time dimension customer order decoupling point" through the rational use of the best resources in product design, manufacturing, assembly, delivery and after-sales service. The so-called "time dimension customer order decoupling point (DCODP)" is a point in the "process" (design process, manufacturing process, assembly process, delivery process and after-sales service process, etc.) of customer order completion, at which point The optimization of the process is no longer based on customer orders, but based on the enterprise's own resource allocation and other conditions. For example, dyeing knitted sweaters with wool is carried out at the time of sale. You can only store undyed wool in the warehouse. What color the customer needs and what color the wool is dyed will undoubtedly greatly reduce the inventory. , That is, the inventory at this time is much less than the inventory required to reserve enough yarns of various colors for customers to choose; in fact, this is a typical example of delaying "time dimension customer orders" through "time dimension" optimization Decoupling point (DCODP)" example. Obviously, the optimization of the "time dimension" is mainly carried out for the operation process, such as the formulation of production plans and various methods of job scheduling.

[0190] To optimize the "time dimension", companies do not adopt a piecemeal approach, but must rethink their product design, manufacturing, and product delivery processes and the configuration of the entire supply chain. By adopting various integration methods, Enterprises can operate with maximum efficiency and meet customer order requirements with minimum inventory.

[0191] ●Space dimension. From a different perspective, it is also called structural dimension or cost dimension. The optimization of product quality and cost is carried out along this dimension, mainly by merging the similarities in different products, components or parts. So as to achieve the purpose of delaying the "customer order decoupling point", such as image 3 As shown, the product model description is generally used here.

[0192] The key to MC's space dimension optimization is to effectively delay the "space dimension customer" by expanding the optimization scope of similar parts, components and products on the basis of fully identifying, sorting and utilizing the similarities in parts, components and products. Order Decoupling Point (SCODP)". Obviously, the promotion and implementation of mass customization in a region or industry can achieve better results than the implementation in only one enterprise, because it can expand the optimization scope of various related resources. For example, various international standards, national standards or industry standards related to product structure description or specification requirements are typical examples. In fact, one of the purposes of the globalization and specialization of manufacturing is to promote the gradual implementation of mass customization on a global scale.

[0193]Obviously, the optimization of "space dimension" is mainly carried out for product composition, such as the selection of general parts, the structural design of customized parts and the selection of basic products for customized products. For the optimization of "spatial dimension", companies cannot use piecemeal methods, but must consider the design, manufacturing, assembly, delivery and after-sales service of customized products based on the entire supply chain of the company. Carrying out all-round optimization, so that enterprises can provide customers with customized (or personalized) products or services at the lowest cost and quality that meets customer requirements.