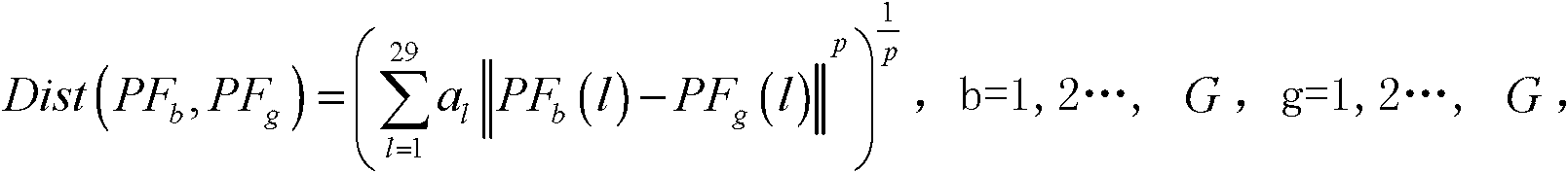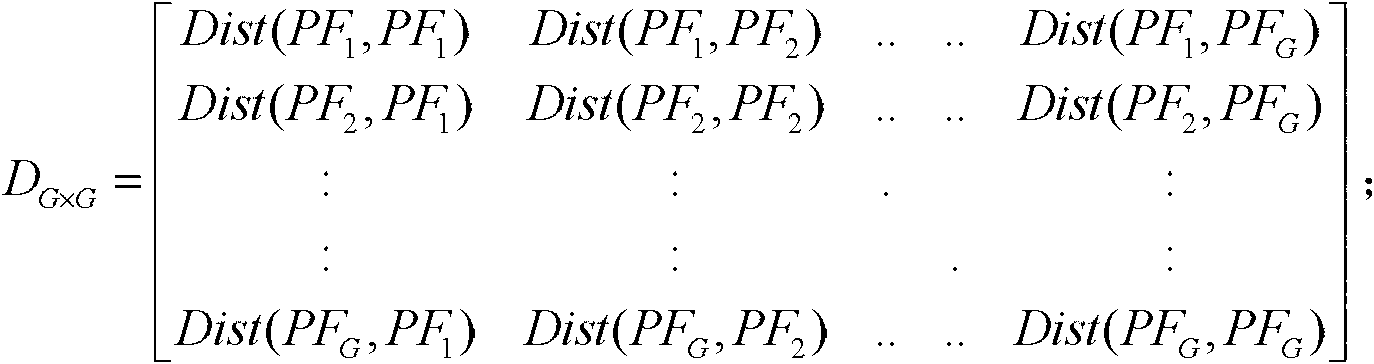Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Detection method for neighbor abnormities of gas turbine

A gas turbine and anomaly detection technology, which is used in engine testing, machine/structural component testing, measurement devices, etc., and can solve the problems of large number of data gas turbines and low efficiency of health status analysis.

Inactive Publication Date: 2012-10-03
HARBIN INST OF TECH
View PDF4 Cites 7 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0004] The present invention aims to solve the problem that the existing gas turbine adopts multiple sensors to collect operation state data, and the analysis efficiency of the health status of the gas turbine is low due to the large number of data, and provides a method for detecting abnormality of the neighbors of the gas turbine

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Detection method for neighbor abnormities of gas turbine
  • Detection method for neighbor abnormities of gas turbine
  • Detection method for neighbor abnormities of gas turbine

Examples

Experimental program
Comparison scheme
Effect test

specific Embodiment approach 1

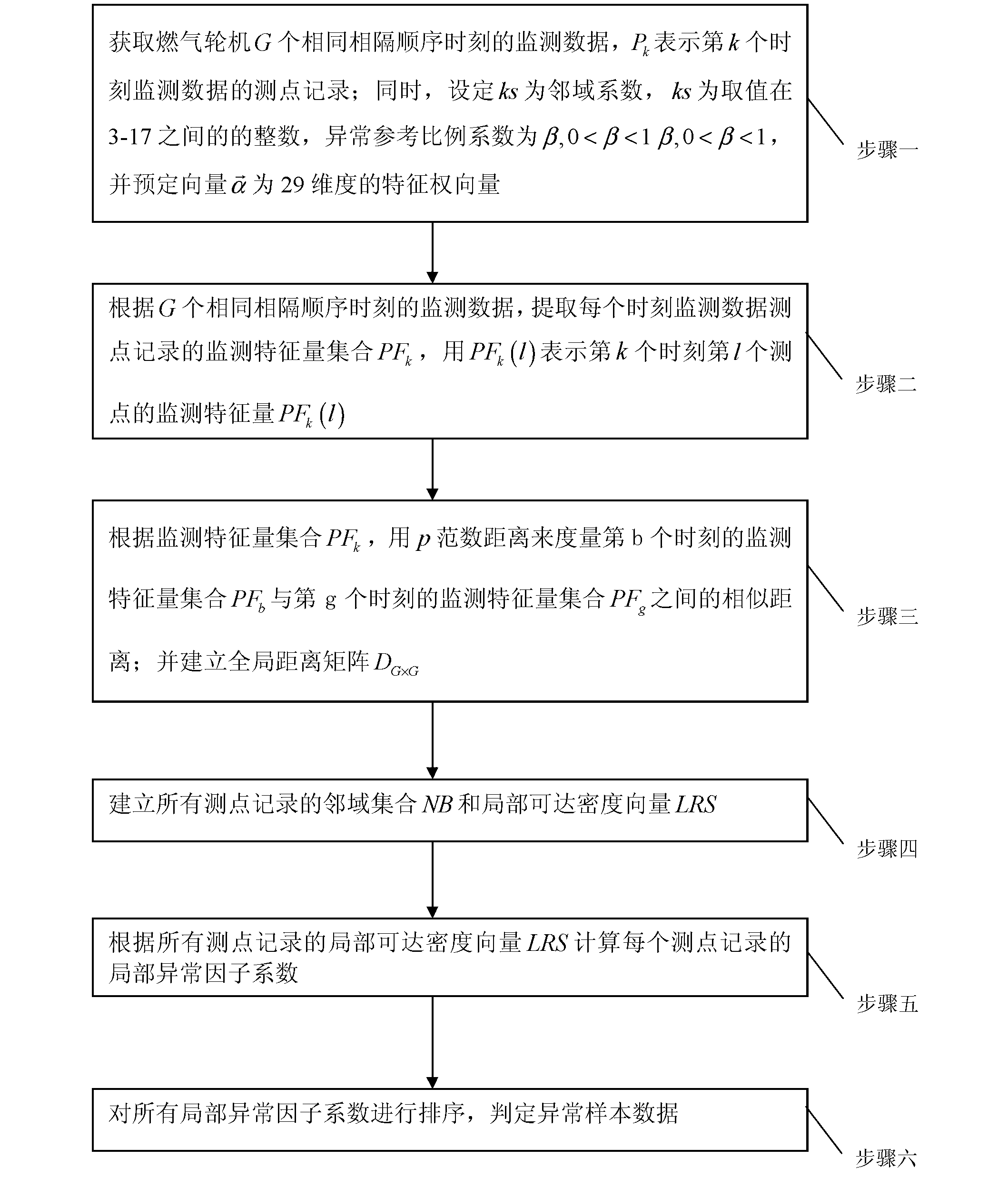
[0038] Specific implementation mode one: the following combination figure 1 Describe this embodiment, the neighbor anomaly detection method of the gas turbine described in this embodiment, it comprises the following steps:

[0039] Step 1: Obtain the monitoring data of G gas turbines at the same interval sequence time, P kIndicates the measurement point record of the monitoring data at the kth moment, G is an integer greater than or equal to 800, k=1, 2, 3...G; at the same time, set kS as the neighborhood coefficient, and kS is the value between 3-17 An integer between , the abnormal reference scale coefficient is β, 0 is a 29-dimensional feature weight vector;

[0040] Step 2: According to the monitoring data of G same interval sequence time, extract the monitoring feature quantity set PF recorded by the monitoring data measuring points at each time k , with PF k (l) Indicates the monitoring feature PF of the lth measuring point at the kth moment k (l), l=1, 2, 3...29;

...

specific Embodiment approach 2

[0054] Specific implementation mode two: this implementation mode is a further description of implementation mode one, and the measurement point record P in step four described in this implementation mode k The neighborhood set of is NB(k) and the local reachable density vector is LRS(k), the method of obtaining is:

[0055] Step 41: Obtain the kth measuring point record P k The ks-th shortest distance with other measuring point records is denoted as LD(k), that is, for

[0056] Dist(PF k , PF 1 ), Dist(PF k , PF 2 ),..., Dist(PF k , PF k-1 ), Dist(PF k , PF k+1 ),..., Dist(PF k , PF G ) are sorted in ascending order, and the distance corresponding to the ksth smallest is LD(k);

[0057] where and the measuring point record P k The nearest ks samples P ω (ω=1, 2, ..., k-1, k+1, ..., G) set is denoted as NB(k):

[0058] NB(k)={P ω , Dist(PF k , PF w )≤LD(k)};

[0059] Step 42: Measuring point record P k The local reachable density vector of LRS(k) is:

[006...

specific Embodiment approach 3

[0061] Specific embodiment three: This embodiment is a further description of embodiment two. The method for calculating the local anomaly factor coefficient recorded at each measuring point in step five of this embodiment is:

[0062] Obtain the local anomaly factor coefficients of all measuring point records, and use LOF(k) to represent the local anomaly factor coefficient of the kth measuring point record, and LOF(k) is expressed as:

[0063] LOF ( k ) = Σ P ω ∈ NB ( k ) LRS ( ω ) ks × LRS ( ...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a detection method for neighbor abnormities of a gas turbine, and belongs to the technical field of state detection of the gas turbine. By adoption of the detection method, the problem that as the existing gas turbine adopts a plurality of sensors to acquire operating state data, the analysis efficiency for the health condition of the gas turbine is low due to more data quantity is solved. The detection method comprises the following steps of: firstly acquiring point measuring records of monitoring data; then extracting monitoring characteristic quantity sets representing different time characteristics; establishing a global distance matrix for measuring the similar distance among sample points at different times; acquiring local reachable density of each sample and a set of neighbourhood sample points from G samples; comparing the local reachable density of all the samples with that of other samples in the neighbourhood and calculating abnormal scores of all the samples; and carrying out sequencing on the number of abnormal score results of the samples, thus obtaining an abnormal sample set. The detection method disclosed by the invention is applicable to detection of neighbor abnormities of the gas turbine.

Description

technical field [0001] The invention relates to a method for detecting an abnormality in the vicinity of a gas turbine, and belongs to the technical field of state monitoring of the gas turbine. Background technique [0002] As an important giant power machine, the gas turbine is more and more widely used because of its compact structure, stable operation, and high thermal efficiency. Due to the high safety and reliability requirements of the gas turbine in operation, in the daily work of the gas turbine, it is necessary to analyze and monitor the health of the unit, analyze and detect various possible abnormal situations, and deal with the failure of the gas turbine in a timely manner. Large-scale failures to avoid irreparable losses. [0003] At present, more sensors are installed on all gas turbines to monitor the working status of the turbines. The data information recorded by the sensor monitoring, such as gas turbine speed, inlet and outlet temperature, etc., is of g...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): G01M15/00G06F19/00
Inventor 贺惠新陈冰冰马超奇于达仁
Owner HARBIN INST OF TECH
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com