Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Implementation method of single-precision floating point trigonometric function covering full circumferential angle

A technology of trigonometric functions and implementation methods, applied in electrical digital data processing, digital data processing components, instruments, etc., can solve problems such as excessive occupation of logic resources, insufficient angular coverage, and reduction of logic resources, and achieve high data throughput. , Improve the working frequency and reduce the effect of logic resources

Inactive Publication Date: 2013-06-12
BEIJING INSTITUTE OF TECHNOLOGYGY
View PDF2 Cites 13 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0006] In view of this, the present invention provides a method for implementing small-area single-precision floating-point trigonometric functions, which solves the problems of insufficient angular coverage and excessive logic resource occupation of the classic CORDIC algorithm, expands the angular coverage, and effectively reduces Reduced logic resources, increased operating frequency

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Implementation method of single-precision floating point trigonometric function covering full circumferential angle
  • Implementation method of single-precision floating point trigonometric function covering full circumferential angle
  • Implementation method of single-precision floating point trigonometric function covering full circumferential angle

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

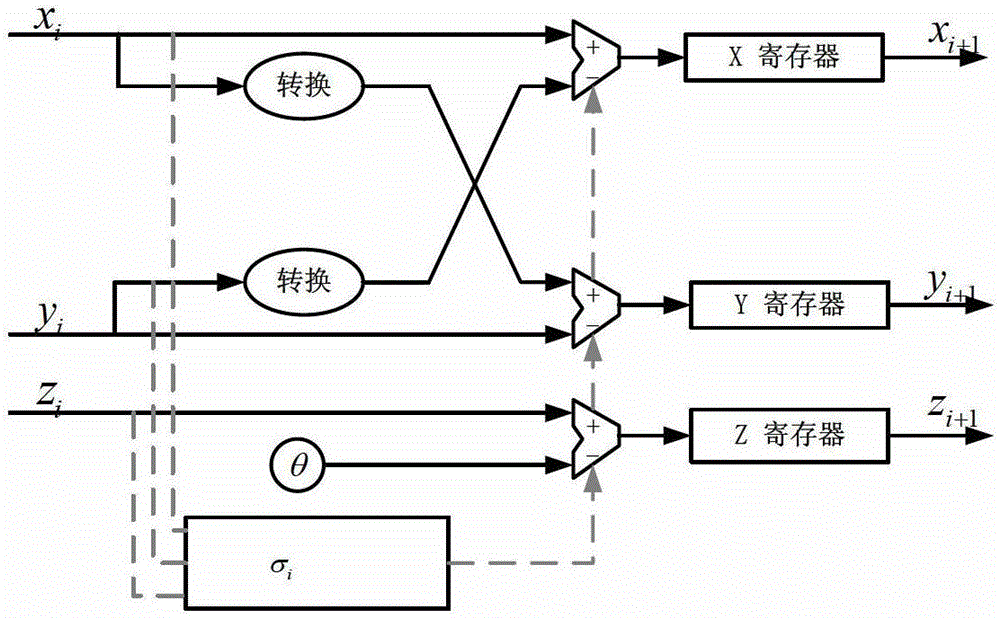
[0038] The present invention is a method for implementing small-area single-precision floating-point trigonometric functions. The method is realized by a system composed of a preprocessing module (CORDIC_PRE), an iterative operation module (CORDIC_CORE) and a postprocessing module (CORDIC_POST). The specific system structure is as follows: figure 1 shown. Specific steps are as follows:

[0039] Step 1. The preprocessing module CORDIC_PRE receives the input single-precision floating-point data, uses the following method to convert the single-precision floating-point data to the circumference range of [-π4,π4], and converts it into high-precision fixed-point data, and converts the obtained high The precision fixed-point data is input to the iterative operation module CORDIC_CORE.

[0040] Because the angular coverage of the classic CORDIC algorithm is not enough, it can only reach [-99.88°, 99.88°]. Considering the calculation accuracy, the present invention chooses to convert ...

Embodiment 2

[0066] This embodiment is still realized by a system composed of a preprocessing module (CORDIC_PRE), an iterative calculation module (CORDIC_CORE) and a postprocessing module (CORDIC_POST).

[0067] Step 1, if the preprocessing module CORDIC_PRE receives the input single-precision floating-point data, use the following method to convert the single-precision floating-point data to the circumference range of [-π4, π4], and convert it into high-precision fixed-point data, the obtained The high-precision fixed-point data is input to the iterative operation module CORDIC_CORE.

[0068] If the input data of the preprocessing module CORDIC_PRE is an angle value θ in the single-precision floating-point data format of any range, add or subtract 2nπ to θ that does not belong to the range of [-2π, 2π], n is an integer, so that θ Converted to the range of [-2π, 2π], then for the case where θ is in the range of [-2π, 2π], record the angle interval where θ is located, as follows:

[0069]...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses an implementation method of single-precision floating point trigonometric function covering full circumferential angle, and belongs to the field of processing of digital signal. The method comprises following steps: firstly, a preprocessing module CORDIC-PRE receives input single-precision floating point data, records the quadrant information of original data, converts the single-precision floating point data within a set angle range into high-precision floating point data, and inputs the high-precision floating point data to an iterative operation module CORDIC-CORE; secondly, the CORDIC-CORE finishes iterative operation of the CORDIC algorithm to the input data by adopting high-precision floating point operation; the result is input to a postprocessing module CORDIC-POST; thirdly, the CORDIC-POST performs quadrant recovery to sine and cosine functional values to be required to be calculated as per the quadrant information recorded in the CORDIC-PRE aiming to the input data; and the data after being recovered is converted into the precision floating point data and output. The implementation method is suitable for actual operation of CORDIC algorithm.

Description

technical field [0001] The invention belongs to the field of digital signal processing, and in particular relates to a method for realizing small-area single-precision floating-point trigonometric functions. Background technique [0002] Modern digital signal processing puts forward higher and higher requirements on the accuracy and dynamic range of operations, and single-precision floating-point trigonometric operations are also used more and more. Coordinate Rotation Digital Calculation (CORDIC) starts with the operation itself, and decomposes complex trigonometric function operations into simple addition, subtraction and shift operations, making trigonometric function operations easy to implement on hardware. [0003] At present, a lot of research has been done on the implementation of single-precision floating-point trigonometric functions at home and abroad. On the basis of the classic CORDIC algorithm, some improvements have been made according to their own needs and a...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): G06F7/544
Inventor 陈禾陈冬于文月谢宜壮曾涛龙腾
Owner BEIJING INSTITUTE OF TECHNOLOGYGY
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com