Graph cut method for contrasting filled and excavated space by using three-dimensional triangulation network

Abstract

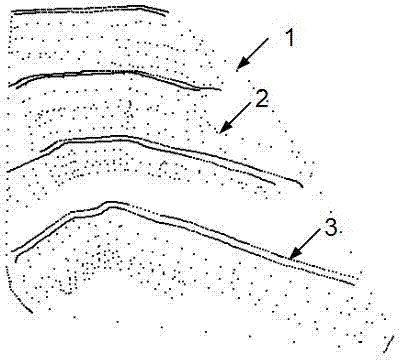
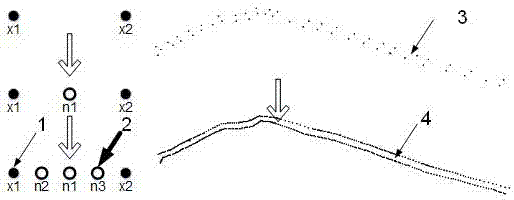
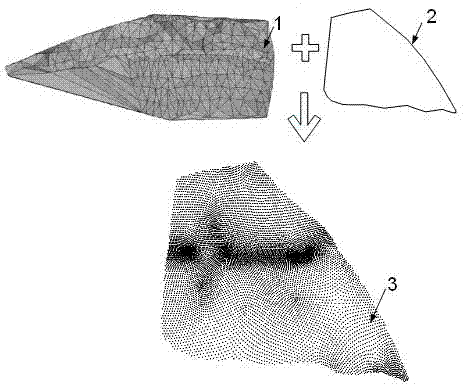
The invention relates to a graph cut method for contrasting filled and excavated space by using a three-dimensional triangulation network. According to the method, the three-dimensional triangulation network is directly constructed on the basis of the graph cut method, and network construction problems are regarded as mark optimization problems. Firstly, initial landform splashes and actual landform splashes are obtained and combined, and then a normal vector of each splash is estimated; tetrahedrons are constructed through the combined splashes by the adoption of the point-by-point insertion algorithm, the space is decomposed, and the tetrahedrons contain the triangulation network which users want to obtain; according to intersecting information of the normal vectors of the splashes and the tetrahedrons, and area information of each triangular surface of the tetrahedrons, the weight of an s-t graph is added; final surfaces are obtained by the minimum cut-maximum flow algorithm, the filled and excavated space is obtained, and the quantity of filled and excavated earth work is obtained by adding up the volumes of the tetrahedrons. According to the graph cut method, projection on a two-dimensional plane is not needed, and the defects caused when the triangulation network is constructed with a two-dimensional projection method are overcome; the quantity of earth work is calculated through the tetrahedrons, so that precision is higher.

Description

technical field [0001] The invention belongs to the field of three-dimensional modeling, in particular to a graph cutting method for constructing a filling and digging space by a three-dimensional triangular network. Background technique [0002] In geotechnical engineering, it is widely involved in the measurement of earth and stone in filled and excavated spaces. The measurement and calculation of earthwork is an important basis for project quantity budgeting, preparation of construction design and reasonable arrangement of construction site in engineering construction. Existing earthwork calculation methods include section method, grid method and DTM method. [0003] The calculation accuracy of the section method is related to the length of the section spacing, the smaller the spacing, the higher the accuracy; when calculating the earth and rock volume by the section method, attention should be paid to the selection of the cross section, which has a great influence on th...

AI Technical Summary

Problems solved by technology

This method has high calculation accuracy, but there are also some problems: when using the projection method to construct the TIN, there are differences in the TIN constructed by different projection surfaces (even wrong TIN), which has a great impact on the accuracy; the projection method cannot be constructed more complicated Realistic model (there is overlap on the projection surface); when calculating the volume with the triangular prism method, the triangular surface will be decomposed, which has a great impact on the accuracy

Images