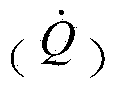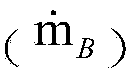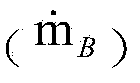Double pinch criterion for optimization of regenerative rankine cycles
A pinch, post-heating technique applied in the field of double pinch criteria for optimization of regenerative Rankine cycles
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
Image
Examples
Embodiment Construction
[0050] The present invention discloses a system and method for optimizing a regenerative Rankine cycle including a double pinch criterion. In some embodiments, the efficiency of the Rankine cycle is enhanced by selecting operational variables such as exhaust pressure and exhaust flow rate such that a feedwater heater achieves a double pinch. In particular, the first pinch is taken at the onset of exhaust steam condensation and the second pinch is taken at the exhaust steam outlet of the feedwater heater. The minimum temperature difference at the first pinch point is substantially equal to the minimum temperature difference at the second pinch point. The present invention discloses a system of regenerative Rankine cycles associated with a double pinch criterion, a method of operating the system and a method of optimizing the operation of the system.
[0051] Some exemplary embodiments will now be described to provide an overview of the invention.
[0052] Based on an understa...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com