Power transmission line equivalent icing thickness monitoring method
A transmission line and ice thickness technology, applied in measuring devices, instruments, etc., can solve the problems of large error in ice thickness, inability to accurately calculate the influence of horizontal wind load transmission lines, inability to accurately collect wind speed and direction, etc.
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
Image
Examples
Embodiment Construction
[0059] The present invention will be described in detail below in conjunction with the accompanying drawings and specific embodiments. This embodiment is implemented on the premise of the technical solution of the present invention, and detailed implementation and specific operation process are provided, but the protection scope of the present invention is not limited to the following embodiments.
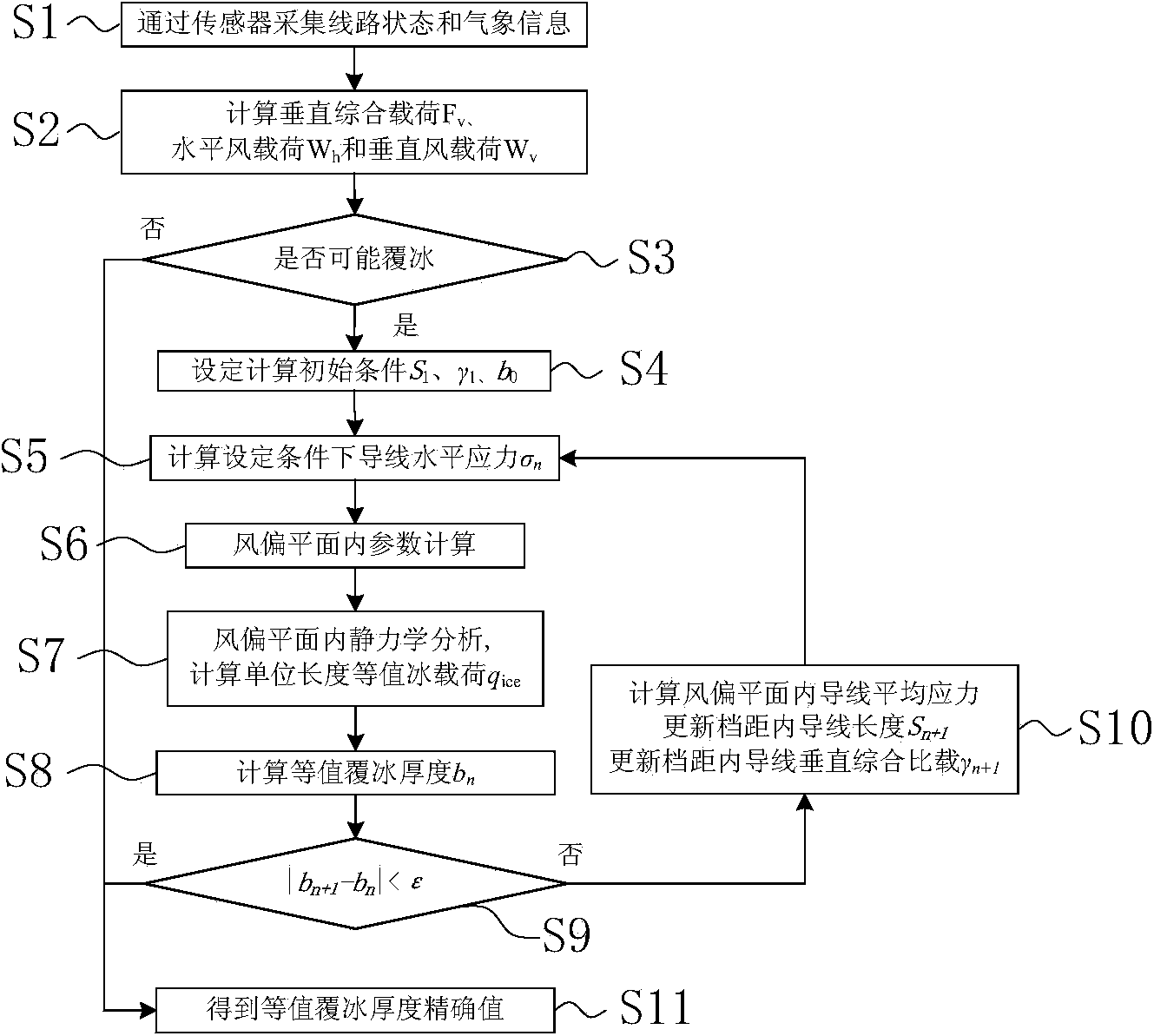
[0060] Such as figure 1 As shown, the transmission line equivalent ice thickness monitoring method provided by the present invention comprises the following steps:
[0061] Step S1, receiving the axial tensile force of the insulator string, the wind deflection angle of the transmission line conductor, the inclination angle of the insulator string, atmospheric temperature, atmospheric humidity, horizontal and lateral Wind speed, horizontal longitudinal wind speed and vertical wind speed.
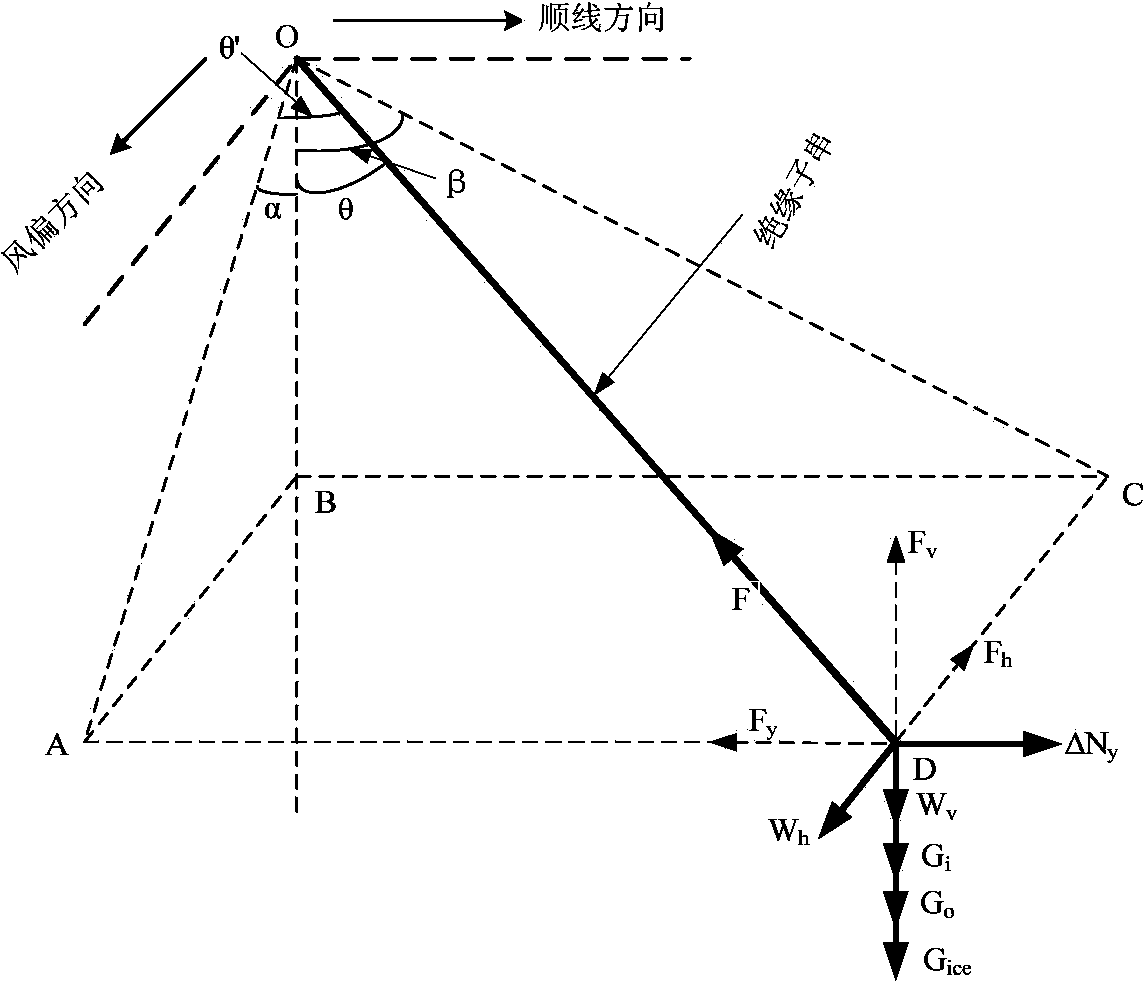
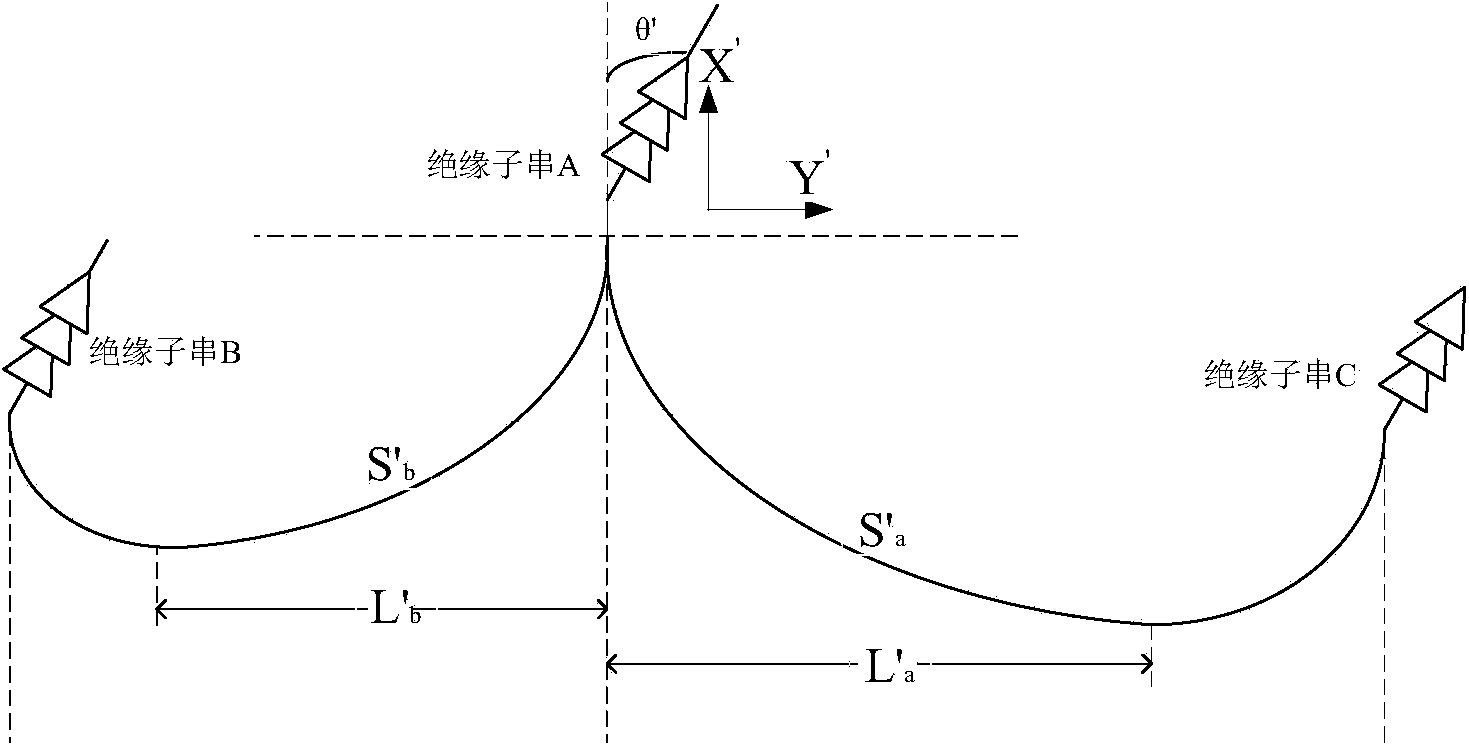
[0062] Step S2, according to the axial tension of the insulator string received in step S1, ...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com