Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

3D model retrieval method and 3D model retrieval apparatus based on slow increment features

A slow-increment feature and 3D technology, applied in character and pattern recognition, special data processing applications, instruments, etc., can solve problems such as sudden changes in feature forms, achieve the effects of reducing difficulty, efficient and accurate retrieval results, and improving matching efficiency

Active Publication Date: 2016-02-10
TIANJIN UNIV
View PDF3 Cites 13 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

Ideally, with the gradual change of the viewing angle, the change of visual features should also be gradual, but in the existing feature extraction methods, the feature form is often mutated

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • 3D model retrieval method and 3D model retrieval apparatus based on slow increment features
  • 3D model retrieval method and 3D model retrieval apparatus based on slow increment features
  • 3D model retrieval method and 3D model retrieval apparatus based on slow increment features

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

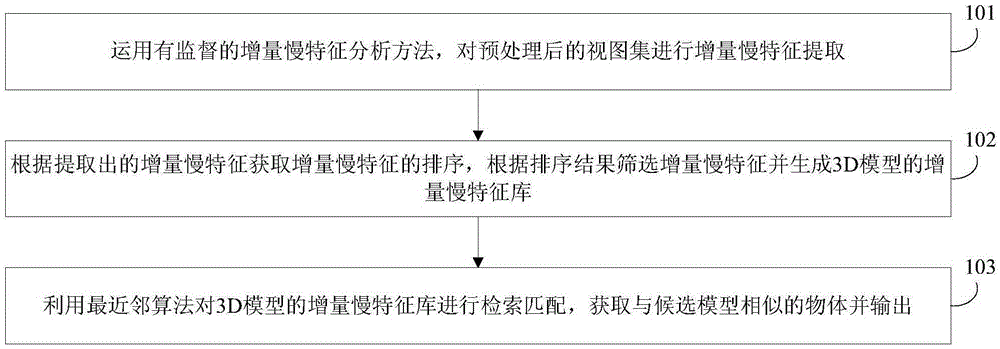
[0049] In order to make model retrieval more accurate, it can improve the efficiency of model retrieval and reduce the impact of external factors on the visual characteristics of the view. See figure 1 , this method includes the following steps:

[0050] 101: Using Supervised Incremental Slow Feature Analysis Methods [6] , perform incremental slow feature extraction on the preprocessed view set;

[0051] 102: Obtain the sorting of incremental slow features according to the extracted slow incremental features, filter the slow incremental features according to the sorting results, and generate a slow incremental feature library of the 3D model;

[0052]103: Use the nearest neighbor algorithm to retrieve and match the incremental slow feature library of the 3D model, and obtain and output objects similar to the candidate model.

[0053] Wherein, the method further includes: acquiring a 2D view set V of objects in the database, and preprocessing the 2D view set so that all 3D mo...

Embodiment 2

[0064] The scheme in embodiment 1 is described in detail below in conjunction with specific calculation formulas and examples, see below for details:

[0065] 201: Obtain the 2D view set V of the object in the database;

[0066] This method mainly uses the retrieval technology based on image comparison, that is, the 3D model is collected from multiple perspectives to form a 2D view set, and the mature 2D technology is used to extract the features of the object. Therefore, each 3D model is represented by multiple views, so the view set can be expressed as where v i Represents the view set of the i-th object; D represents the feature dimension of the view; f k Indicates the kth viewing angle of an object; N indicates the number of 3D models; M indicates the number of views of each 3D model; Indicates the scope to which each object's view collection belongs.

[0067] 202: Perform normalized preprocessing on the view set, so that the view sizes of all 3D models are consisten...

Embodiment 3

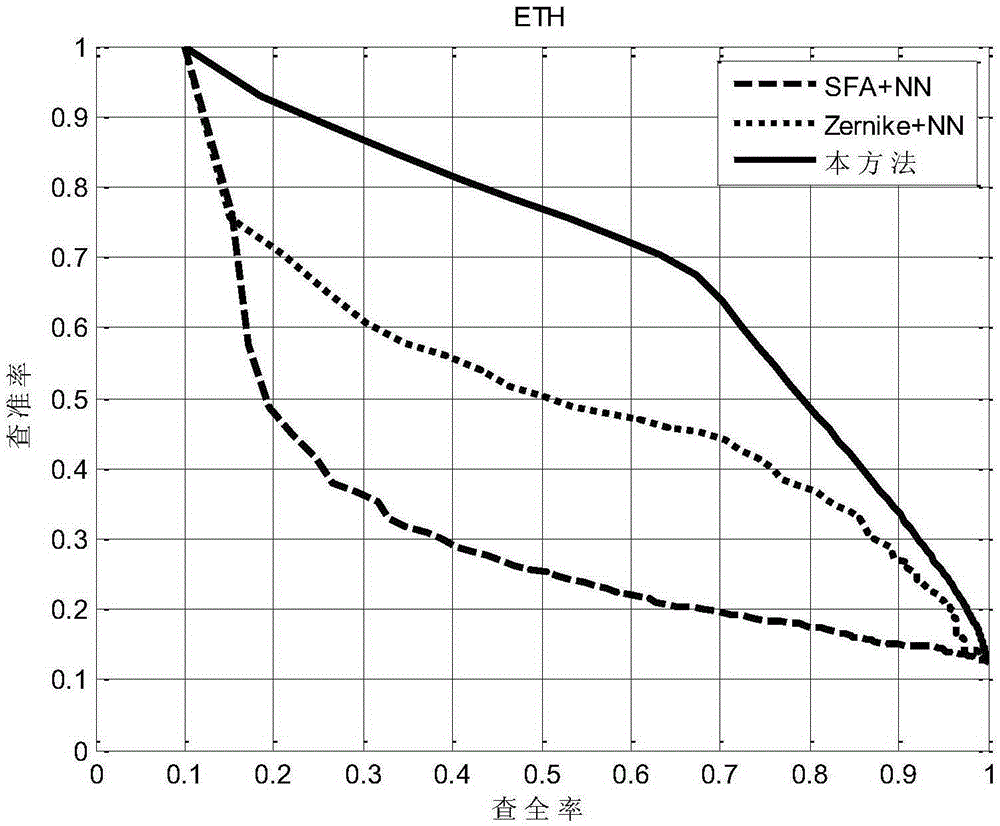
[0114] In this experiment, the embodiment of the present invention adopts the existing, online shared, more commonly used Zurich Federal Institute of Technology (German name The Technische Hochschule Zürich (ETH for short) database and the Taiwan University of China (NTU for short) database were used for experiments. The ETH database was relatively small and the models were more standardized, including 80 3D models, with a total of 8 categories and 10 objects in each category, namely apples and cars. , cow, mug, puppy, horse, pear, tomato. The NTU database has a total of 549 objects, 47 categories, and the number of objects in each category varies. The database is a virtual model database, and images are captured through 3D-MAX. This laboratory uses 60 virtual cameras to acquire images from different perspectives , each object obtains 60 views of different viewing angles, wherein the number of virtual cameras, that is, the shooting angle, can be set according to experimental ...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The present invention discloses a 3D model retrieval method and a 3D model retrieval apparatus based on slow increment features. The method comprises: carrying out slow increment feature extraction to a preprocessed view set by applying a supervised slow increment feature analysis method; acquiring a sorting result of the slow increment features according to the extracted slow increment features, screening the slow increment features according to the sorting result and generating a slow increment feature library of a 3D model; and carrying out retrieval matching on the slow increment feature library of the 3D model by using a nearest neighbor algorithm to acquire and output an object that is similar to a candidate model. The apparatus comprises: an extraction module, an acquisition module, a generation module and a matching and outputting module. According to the method and the apparatus, the feature extraction difficulty of a nonrigid model is reduced, the stability and accuracy of feature extraction are improved, a good condition is provided for the subsequent 3D model retrieval, and the retrieval result is guaranteed to be more efficient and accurate.

Description

technical field [0001] The invention relates to the field of image retrieval, in particular to a 3D model retrieval method and retrieval device based on incremental slow features. Background technique [0002] With the widespread use and dissemination of 3D models, as well as the development of computer graphics and spatial visualization technology, 3D models have been used in various aspects of social life, such as virtual reality, 3D animation and games, CAD, military, molecular biology, etc. 3D model has become the fourth multimedia data type after sound, image and video. At present, there are trillions of 3D models, and a large number of 3D models are generated and disseminated every day, so there is an urgent demand for 3D model retrieval. Commonly used 3D model retrieval techniques are divided into text-based retrieval and content-based retrieval. [0003] The algorithm of text-based retrieval technology is simple, and has been quite mature after years of development...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): G06F17/30G06K9/62
CPCG06F16/583G06F18/22
Inventor 刘安安苏育挺李晓雪
Owner TIANJIN UNIV
Features
  • Generate Ideas
  • Intellectual Property
  • Life Sciences
  • Materials
  • Tech Scout
Why Patsnap Eureka
  • Unparalleled Data Quality
  • Higher Quality Content
  • 60% Fewer Hallucinations
Social media
Patsnap Eureka Blog
Learn More

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com