Two-dimensional dispersive medium Crank-Nicolson complete matching layer implementation algorithm based on DG algorithm
A completely matched layer and dispersive medium technology, which is applied in the field of Crank-Nicolson completely matched layer realization algorithm of two-dimensional dispersive medium, and can solve the problems of increased numerical dispersion, unsatisfactory performance, and low calculation accuracy of the algorithm.
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
Image
Examples
Embodiment Construction
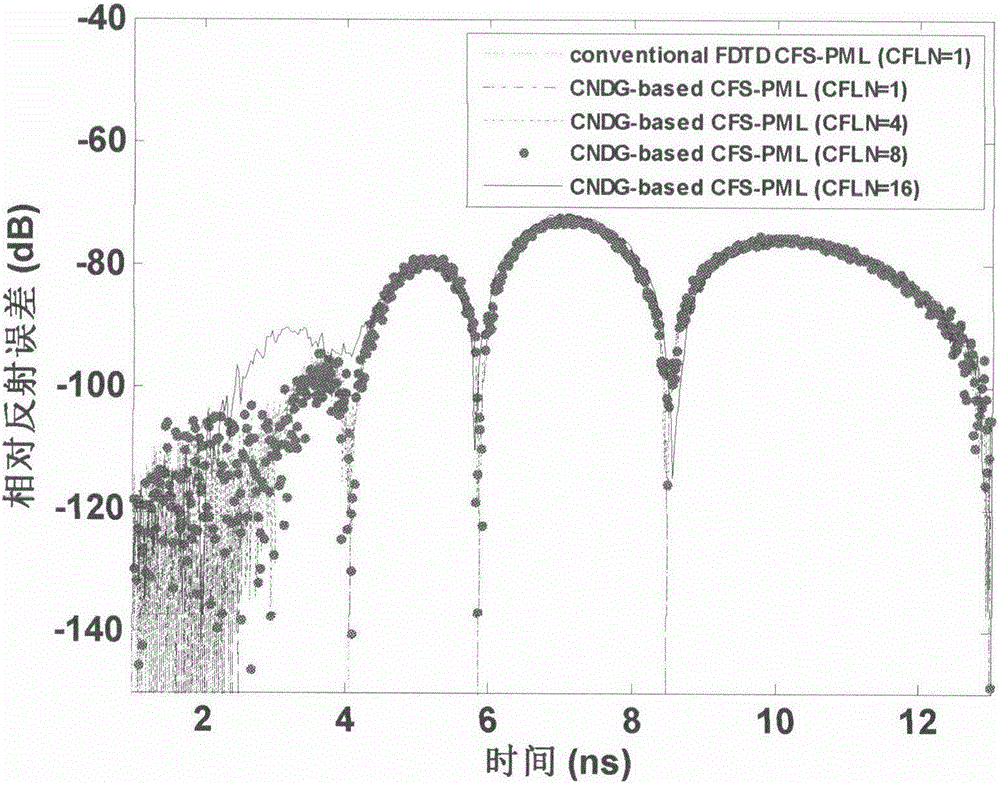
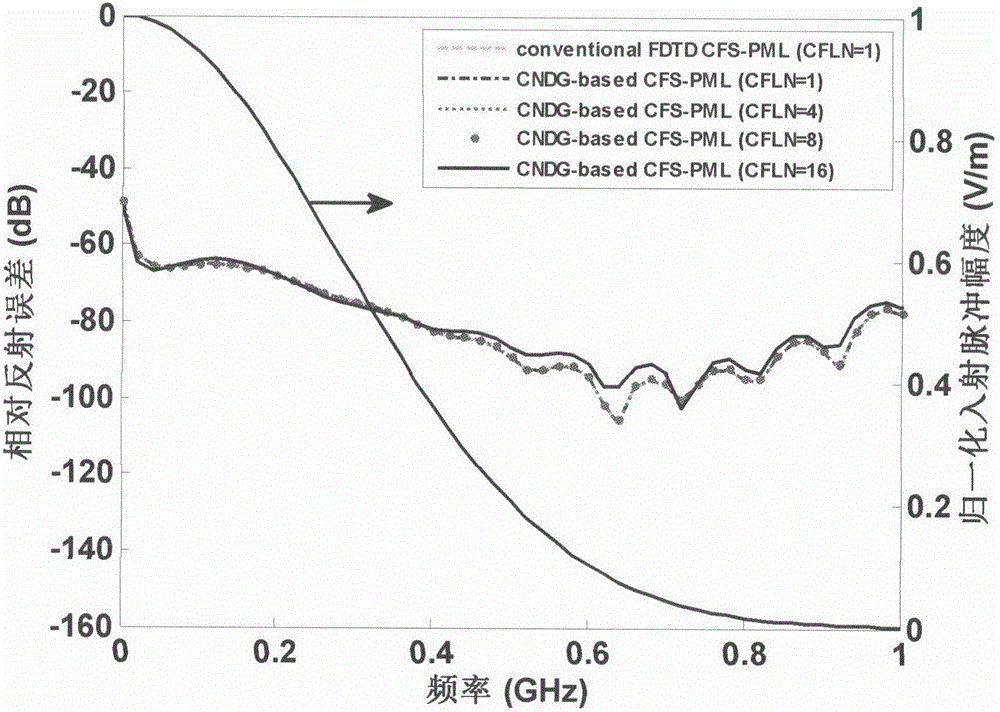
[0024] The gist of the present invention is to propose a two-dimensional dispersive medium Crank-Nicolson complete matching layer realization algorithm based on DG algorithm, and use the Douglas-Gunn solution idea to greatly improve the electromagnetic field calculation speed.
[0025] The embodiments of the present invention will be further described in detail below in conjunction with the accompanying drawings.
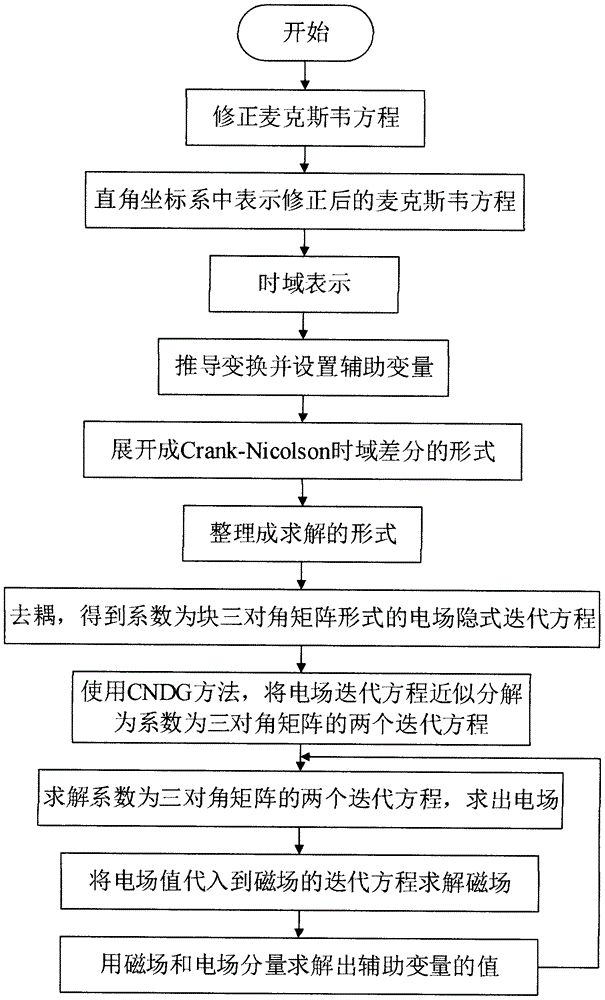
[0026] figure 1 It is a flowchart of the present invention, and the specific implementation steps are as follows:
[0027] Step 1: Correct Maxwell’s equations in the frequency domain to Maxwell’s equations with a stretched coordinate operator, and express the corrected Maxwell’s equations in the frequency domain in a Cartesian coordinate system; for the dispersion medium item, use the auxiliary differential equation method to set Auxiliary variable; TM wave propagation in a linearly dispersive medium can be described as
[0028] - jωH...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com