Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Image orthogonal moment numerical stability analyzing method

An analysis method and stability technology, which is applied in the field of numerical stability analysis of image orthogonal moments, can solve problems such as limiting the application of orthogonal moments, troublesome technical personnel, etc.

Inactive Publication Date: 2017-03-15
HUBEI UNIV OF TECH
View PDF3 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

Due to the absence of a rigorous numerical error stability evaluation system, the application of orthogonal moments in large-scale image pattern recognition and reconstruction is greatly limited.
[0004] The evaluation of the current orthogonal moment calculation method is verified by a small number of experiments. It cannot be confirmed under what conditions it converges, and under what conditions it does not converge, so it brings more business troubles to technicians.

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Image orthogonal moment numerical stability analyzing method
  • Image orthogonal moment numerical stability analyzing method
  • Image orthogonal moment numerical stability analyzing method

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

[0055] This embodiment discloses a method for analyzing the numerical stability of image orthogonal moments, including the following steps:

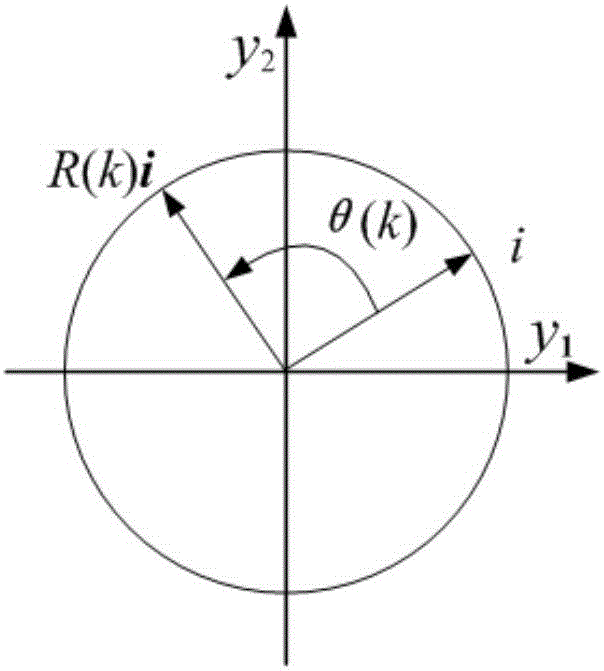
[0056] (1) Analyze the reasons for the instability of the three-term recursive formula of the orthogonal polynomial;

[0057] The three-term recursive formula is as follows:

[0058] P k (x)=A k (x)P k-1 (x)-B K (x)P k-2 (x)=(α k x-ω k )P k-1 (x)-γ k P k-2 (x) (1-1)

[0059] Among them, P k (x),P k-1 (x) and P k-2 (x) are nth order, n-1th order and n-2th order discrete orthogonal polynomials respectively, A k (x) and B k (x) is the iteration coefficient.

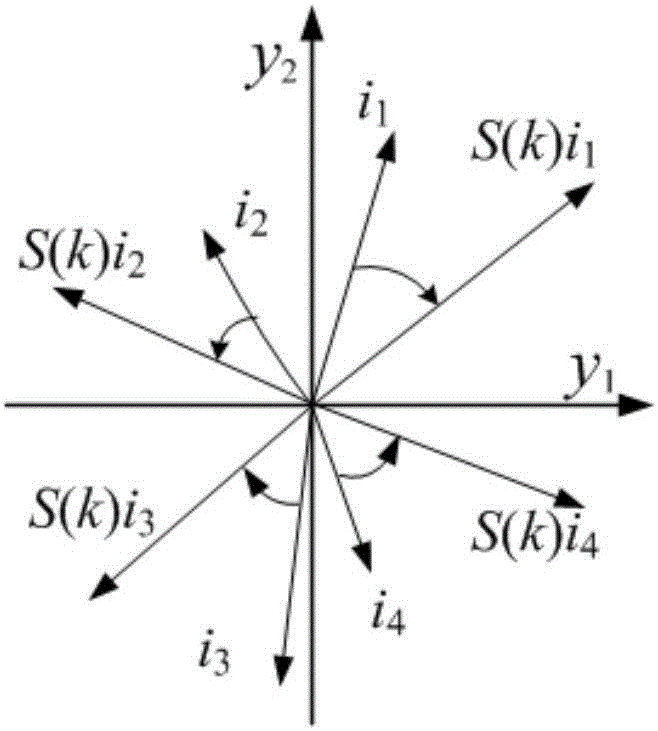
[0060] In the actual computer operation process, the truncation error occurs due to the determination of the number of digits in the system, which makes the observed value deviate from the actual value. This truncation error varies throughout the recursion, potentially affecting the confidence in our observed expected value. Therefore, it is necessary to analyze the n...

Embodiment 2

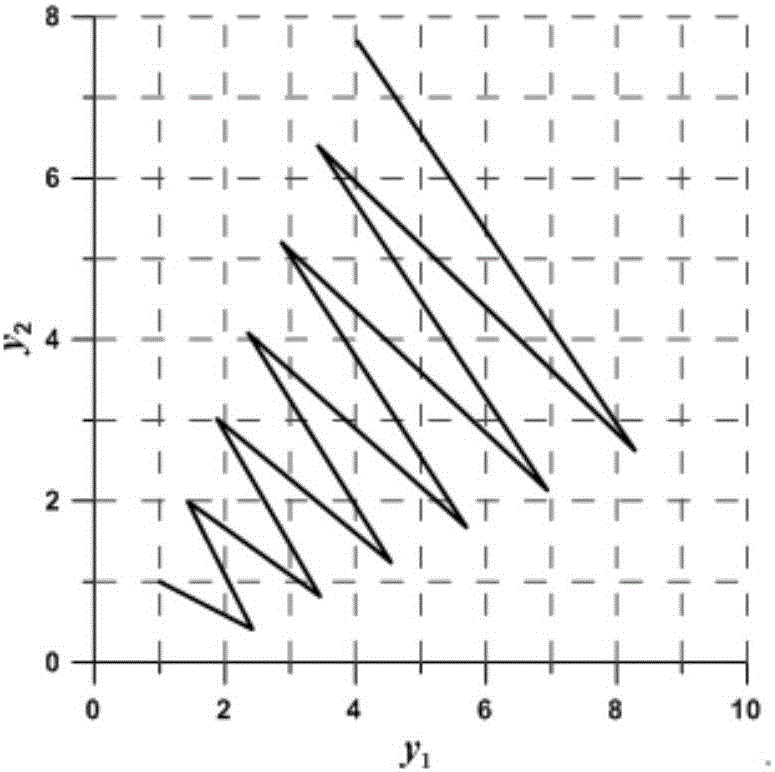
[0118] This embodiment discusses the instability analysis in the recursive calculation of continuous orthogonal Legendre polynomials, discrete orthogonal Tchebichef polynomials and discrete orthogonal Krawtchouk polynomials.

[0119] (1) Stability analysis of Legendre polynomial recursive calculation:

[0120] The three-term recursive formula for the Legendre polynomial:

[0121]

[0122] According to the first instability theorem, redefine the variable y 1 (k)=L(k),y 2 (k)=L(k+1), then formula (1-15) can be written as:

[0123] Y(k)=(y 2 (k),y 1 (k)) T =G(k)Y(k-1) (2-2)

[0124] and

[0125] For Legendre polynomials there is A x (k)=(2k-1)x / k and B(k)=(k-1) / k,

[0126] Suppose the element q of the asymptotically positive definite matrix Q 11 (k)>0,q 12 (k)≤0 and q 22 (k)>0 and considering that it has a solution P, formula (13) can be expressed as:

[0127]

[0128] If you specify q 11 (k)=μ>0,q 22 (k)=ν>0,q 12 (k)=q 21 (k)=0 and the symmetric matrix P...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses an image orthogonal moment numerical stability analyzing method, which belongs to the image processing and mode recognizing field. Based on the discrete control theory, the three recursive formulas of an orthogonal polynomial are transformed into the variable coefficient differential equations for the order k, that is, the zero input response of a discrete linear time-varying system is discussed; and through the use of the SVD decomposition of a matrix, the original state equation is transformed as an equivalent state equation constructed by a rotation matrix and a diagonal matrix. Based on the Lyapunov theorem, two new instabilities are derived. With the method, the problem with the instability of the orthogonal moments caused by the divergence of the orthogonal polynomials is solved in the calculation process of the orthogonal moments of three recursive formulas; and the root causes of the recursive computational instability of the classical Tchebichef and Krawtchouk polynomials are found so as to provide reference for future research.

Description

technical field [0001] The invention belongs to the field of image processing and pattern recognition, in particular to a numerical stability analysis method for image orthogonal moments. Background technique [0002] As an important technical means in the field of image analysis and pattern recognition, orthogonal moments have many advantages compared with classical geometric moments, such as 1) Orthogonality: that is, the original image can be perfectly reconstructed in theory, so in the field of image analysis Among them, it has a better application prospect than geometric moments; 2) invariance: that is, orthogonal moments have multi-distortion invariance such as translation, rotation, scale, and stretching; 3) low noise sensitivity: moments with strong noise suppression ability In order to better describe the image, the moment value of the orthogonal moment is not sensitive to noise and can accurately describe the image features. Therefore, with the development of mome...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): G06T7/00
CPCG06T7/00
Inventor 范秀香陈卓付波刘济源赵远阳权轶何莉
Owner HUBEI UNIV OF TECH
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com