Error Correction Method of Geomagnetic Vector Measurement System Based on Lagrangian Multiplier Method
A measurement system and error correction technology, applied in the field of magnetic measurement, can solve problems such as reducing the accuracy of error calibration, failing to meet the requirements of geomagnetic vector measurement accuracy, and affecting the accuracy of parameter estimation.
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
Image
Examples
Embodiment Construction
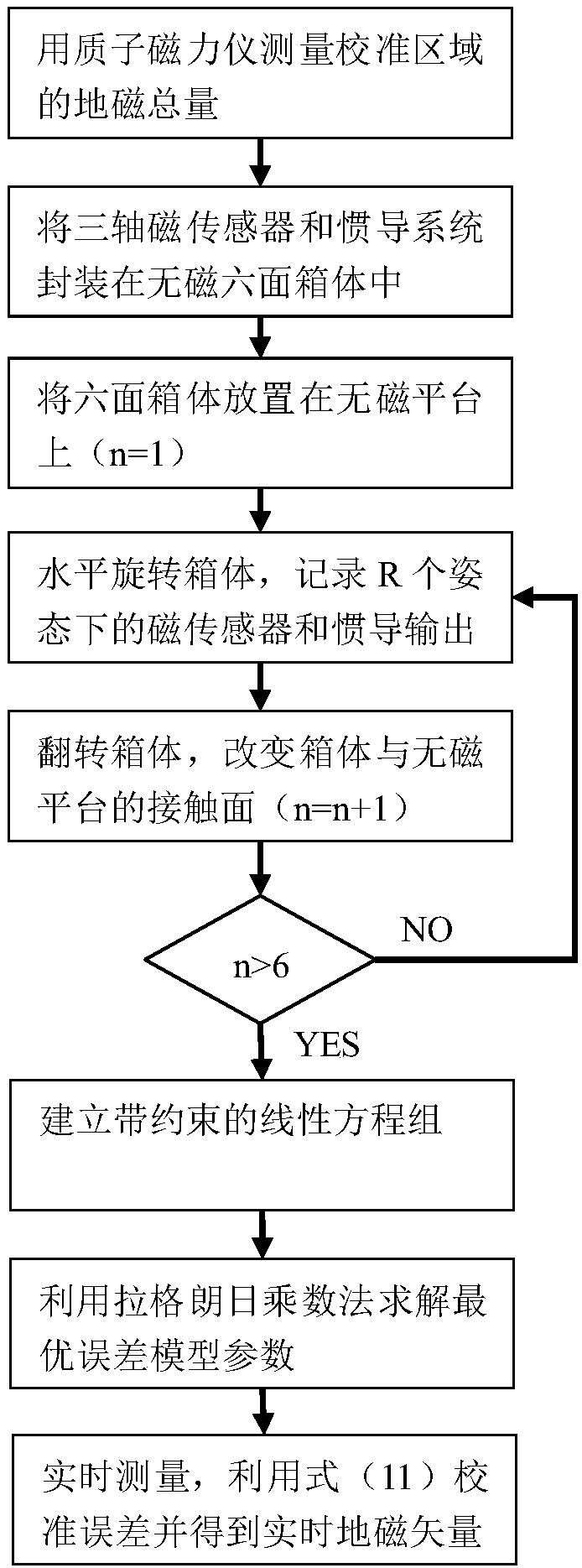
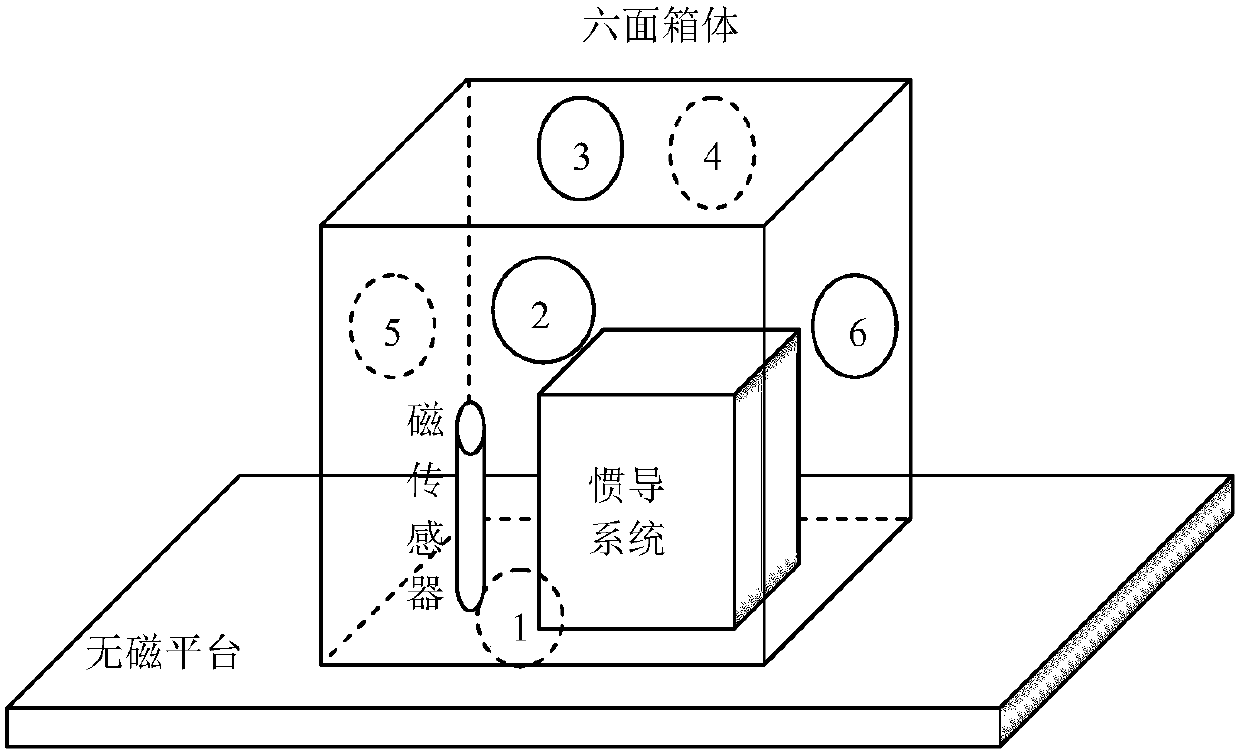
[0074] Hereinafter, the present invention will be further described with reference to the accompanying drawings and specific embodiments.
[0075] 1. Set the simulation conditions and carry out the simulation test of the present invention.
[0076] 1) Set the geomagnetic field vector of the test area as B e =[35200 -33155 -2000]nT (under the geographic coordinate system, according to the global geomagnetic model, the projected vector value of the geomagnetic field vector under the geographic coordinate system can be calculated); the proton magnetometer measures the total amount of geomagnetism above the non-magnetic platform for T e =48397nT.
[0077] 2) According to prior knowledge, preset the values of some parameters in the measurement system (under the magnetic sensor coordinate system), specifically:
[0078] 3) The Euler angles between the magnetic coordinate system and the inertial navigation coordinate system are: [α 0 beta 0 γ 0 ]=[8-5 3] degrees.
[0079...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com