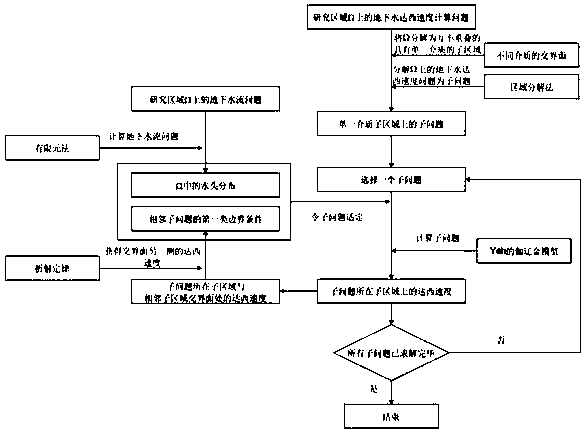
Domain decomposition finite element method for simulating Darcy velocity at interface of groundwater medium

A technology of domain decomposition and finite element method, applied in the field of hydraulics, it can solve the problems of insufficient Darcy speed and low efficiency, and achieve the effect of reducing calculation time and improving calculation efficiency.

Active Publication Date: 2019-09-03
NANJING UNIV
View PDF3 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0006] In view of this, the object of the present invention is to provide a kind of regional decomposition finite element method of simulating the Darcy velocity at the interface of groundwater medium, to solve the low efficiency and the Darcy velocity at the interface of different media in the prior art when calculating the Darcy velocity The speed does not meet the problem of the law of refraction. The method of the present invention reduces the calculation consumption of Darcy velocity through the area decomposition method, and applies the law of refraction to ensure the accuracy of the Darcy velocity at the interface.

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Domain decomposition finite element method for simulating Darcy velocity at interface of groundwater medium
  • Domain decomposition finite element method for simulating Darcy velocity at interface of groundwater medium
  • Domain decomposition finite element method for simulating Darcy velocity at interface of groundwater medium

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

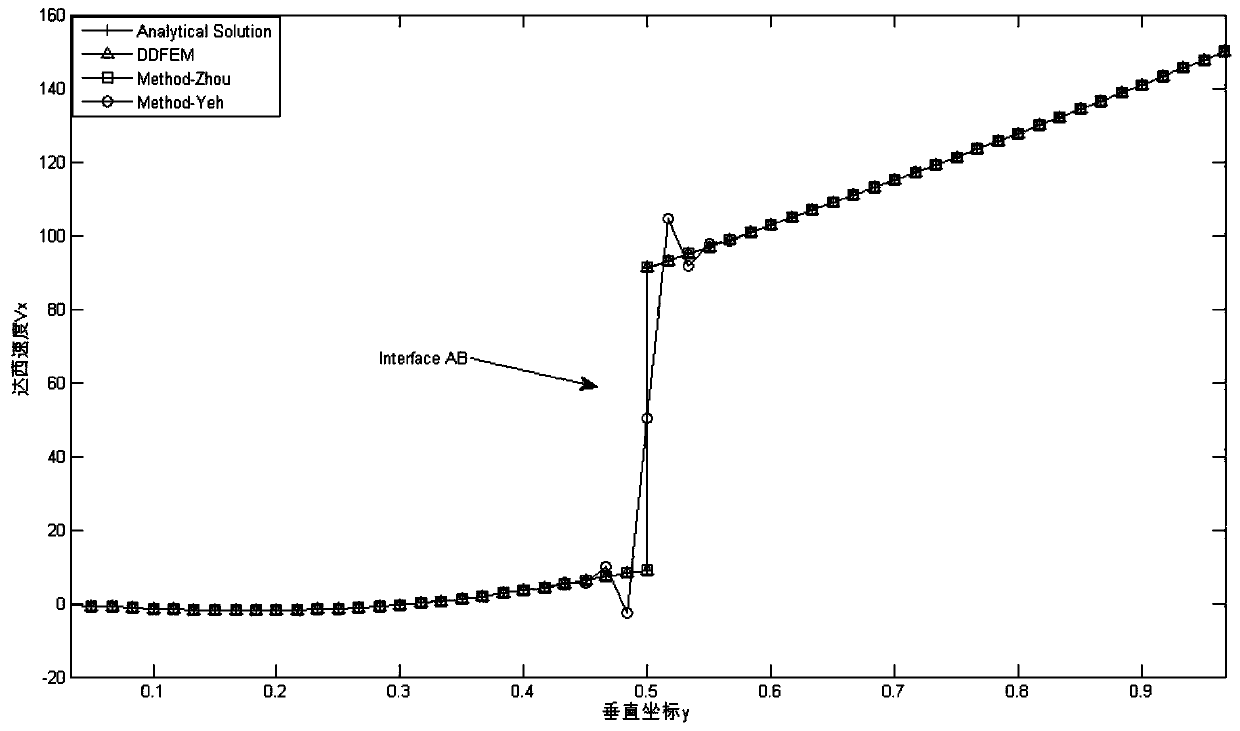
[0102] Example 1: 2D Steady Flow Model with Interfaces Parallel to Coordinate Axes

[0103] Research area such as figure 2 As shown, the equations of groundwater flow and Darcy velocity are (6) and (7) respectively. The research area Ω=[0,1]×[0,1]. The study area contains two different media, which can be divided into two sub-areas by the interface AB (y=0.5). The permeability coefficients of the two sub-areas are: zone 1:K 1x =(1+x)(1+y), K 1y = 10(1+x)(1+y), zone 2:K 2x =10(1+x)(1+y),K 2y =100(1+x)(1+y). This example has an analytical solution:

[0104] Head:

[0105] V x:

[0106] In this example, the source-sink term W and the first type of boundary conditions are given based on the analytical solution of the water head.

[0107] The study area is divided into 7200 units by a triangular grid, the water head is solved by FEM, and the velocity is solved by DDFEM, Method-Zhou and Method-Yeh.

[0108] The Darcy velocity V of each method at the section x=0.5 of ...

Embodiment 2

[0111] Example 2: 2D Steady Flow Model with Interfaces Not Parallel to Coordinate Axes

[0112] Research areas such as Figure 5 As shown, the equations of groundwater flow and Darcy velocity are (6) and (7) respectively. The research area Ω=[0,120m]×[0,120m] is divided into three sub-areas by the medium interface AB (y=20m) and CD (x+y=160m), and the source-sink term W is 0. The left and right boundaries of the study area are constant water head boundaries, 0m and 1m, respectively, and the upper and lower boundaries are water-isolated boundaries. The study area in this example is an isotropic medium, that is, the permeability coefficients in the x and y directions are equal. The permeability coefficients of the three sub-regions zone 1-zone3 are: 100m / d, 10m / d, 100m / d. Since there is no analytical solution for this example, the solution of Method-Zhou-F will be used as a standard control.

[0113] Method-Zhou-F divided the study area into 18432 triangular units, and appli...

Embodiment 3

[0116] Example 3: 2D Steady Flow Model with Intersecting Interfaces

[0117] Research area such as Figure 11 As shown, the equations of groundwater flow and Darcy velocity are (6) and (7) respectively. Research area Ω=[0,1]×[0,1]. The interface AB (y=0.5) and CD (x=0.5) intersect at point o, which divides the study area into 4 sub-areas, and the permeability coefficients of zone1-zone 4 are 1, 10, 10, and 100, respectively. This example has analytical solutions, where the analytical solutions of zone 1 and zone 3 are the analytical solutions of zone 1 and zone 2 in embodiment 1, respectively. And the analytical solution head of zone 2 and zone 4 is:

[0118]

[0119]

[0120] In this example, the source-sink term, Darcy velocity, and the expressions of the first-type boundary conditions can all be given based on the hydraulic coefficient and the analytical solution head.

[0121] In this example, DDFEM, DDFEM-AS, Method-Yeh, and Method-Yeh-AS are used to solve the p...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to view more

PUM

No PUM Login to view more

Abstract

The invention discloses a domain decomposition finite element method for simulating Darcy speed at an underground medium interface. The method comprises the following steps: performing variation on anunderground flow problem by using a Galerkin method, sub-dividing a research domain, and acquiring waterhead by applying the finite element method; decomposing the research domain into a plurality ofsingle-medium sub-domains by applying interfaces of different mediums according to the medium composition of the research domain, and decomposing an underground Darcy speed solution problem on the research domain into sub-problems on the sub-domain by applying the domain decomposition method; selecting one sub-problem, performing variation by using the Galerkin method, and acquiring the Darcy speed by applying a Galerkin model of the Yeh, acquiring the Darcy speed at the other side of the interface of the sub-domain and other sub-domain by combining with the refraction law as the first classof boundary condition of the adjacent sub-problem; selecting the next sub-problem to solve, and repeating this process until all sub-problems are completely solved. By using the method disclosed by the invention, the computing consumption of the Darcy speed is reduced through the domain decomposition method, and the precision of the Darcy speed at the interface is guaranteed by using the refraction law.

Description

technical field [0001] The invention belongs to the technical field of hydraulics, and in particular relates to a regional decomposition finite element method for simulating the Darcy velocity at the interface of groundwater media. Background technique [0002] Groundwater is an important part of water resources and an important resource for human survival. The velocity and flow of groundwater can accurately describe the movement state of groundwater, which is of great significance to groundwater problems, especially solute transport problems. Therefore, it is of great significance to develop an accurate and efficient groundwater Darcy velocity algorithm for the investigation of groundwater numerical simulation. [0003] Most groundwater media in nature are heterogeneous, and factors such as groundwater interface, cracks, and lenses will affect the heterogeneity of groundwater media. When simulating many groundwater problems in nature, the research area can be divided into...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to view more

Application Information

Patent Timeline
no application Login to view more
Patent Type & Authority Patents(China)
IPC IPC(8): G06F17/50
CPCG06F30/23
Inventor 谢一凡吴吉春薛禹群谢春红
Owner NANJING UNIV
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Try Eureka
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap