Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

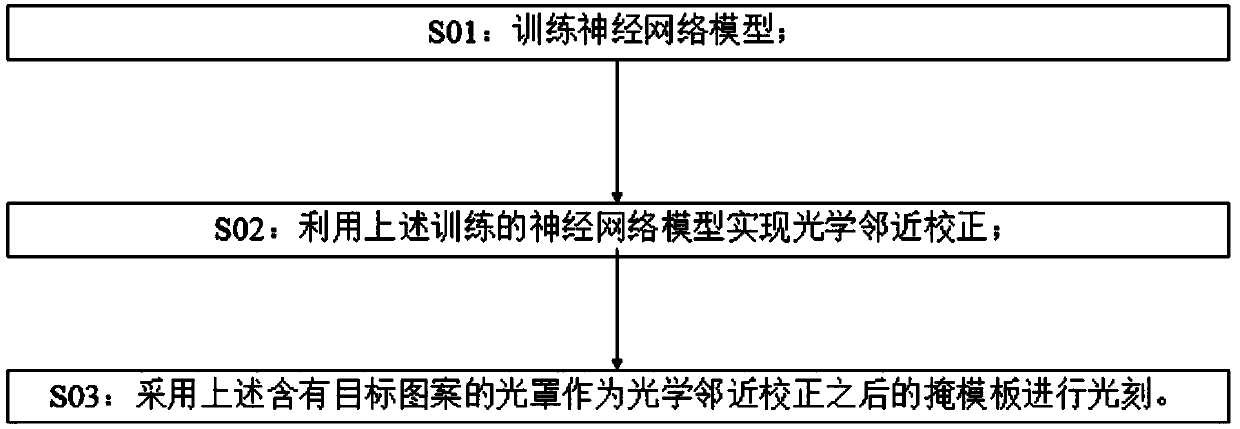
Neural network model-based optical proximity correction method

A neural network model and optical proximity correction technology, applied in the field of optical proximity correction based on neural network model, can solve the problems of increased computing time, impractical full-chip implementation, etc., and achieve the effect of computing improvement

Active Publication Date: 2018-04-13
SHANGHAI INTEGRATED CIRCUIT RES & DEV CENT
View PDF6 Cites 19 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

All inverse lithography methods have a large increase in computation time, therefore full-chip implementations of inverse lithography solutions remain impractical

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Neural network model-based optical proximity correction method
  • Neural network model-based optical proximity correction method
  • Neural network model-based optical proximity correction method

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

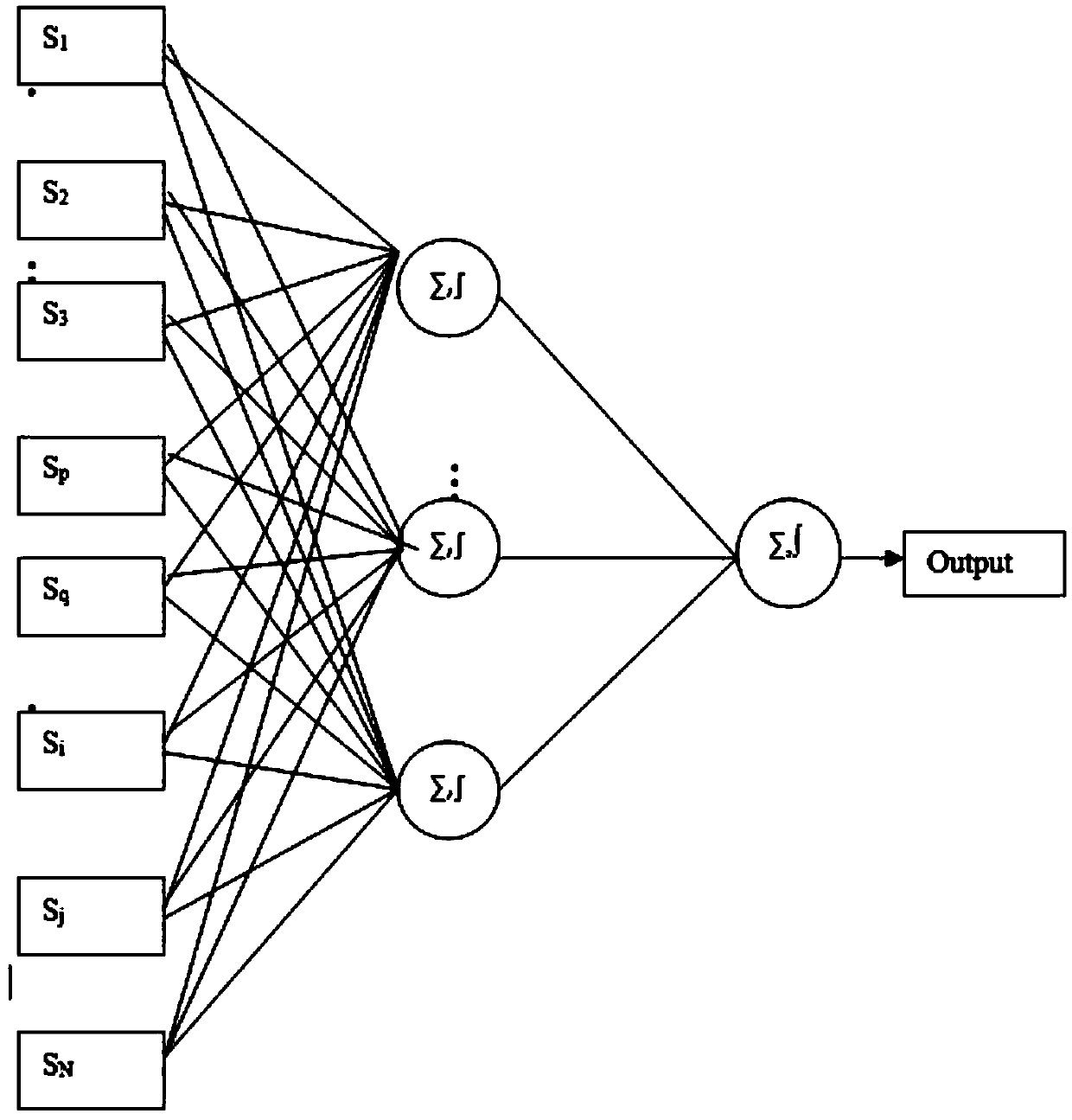
[0057] When the neural network model is a linear neural network model, the required photolithographic mask pattern, that is, the auxiliary pattern and the corrected pattern of the main pattern, can be regarded as at a certain threshold, by cutting a continuous class intensity function and the obtained contour. This class of intensity functions can be derived from the optical image intensity function I(x,y) of the lithographic target pattern via a fixed nonlinear mapping mechanism. Obviously, It not only depends on I(x, y), but also depends on the gray distribution of the optical image intensity function I(x, y) around the (x, y) point. The most efficient way to encode the gray level distribution of the optical image intensity function I(x,y) around the point (x,y) is to use a set of values ​​of the intrinsic imaging signal at the point (x,y). In order to accurately describe the optical image intensity including 3D effects of lithographic masks, the intrinsic imaging signal...

Embodiment 2

[0083] When the neural network model is a quadratic neural network model, as attached Figure 4As shown, the lithographic mask plane is divided into small units, assuming that t(i, j) and t(m, n) are behind the small unit (i, j) and small unit (m, n) lithographic mask light field. Since the response of chemical photoresists is the light intensity, not the light field itself, we can imagine that the target pattern calculated from the reverse lithography technique can be cut by a continuous intensity-like function of and the obtained contour. . This function only depends on all pair values ​​{t(i,j),t(m,n)}, but the function itself is unknown:

[0084]

[0085] Pairs {t(i,j),t(m,n)} are defined around the point (x,y). {t(i,j),t(m,n)} are real quantities because all lithography mask types in use today have only phase 0 or phase 180. One way to explore this unknown function is to use a multi-layer perceptron neural network model, with the set {t(1,1)*t(1,1),t(1,1)*t(1,2),...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a neural network model-based optical proximity correction method. The neural network model-based optical proximity correction method comprises the following steps of S01, training a neural network model, wherein M test patterns are selected on a training optical mask, target patterns corresponding to the M test patterns are respectively obtained, a similar strength functionI-bar (X, Y) is simulated by a known perception neural network, and the perception neural network is trained according to the similar strength function and the target patterns to obtain the neutral network model; and S02, achieving optical proximity correction by the trained neutral network model, in which the similar strength function I-bar (X, Y) of an optical mask to be processed is obtained by the obtained neutral network model, the similar strength function I-bar (X, Y) is cut by a cutting threshold to generate the optical mask containing the target patterns, and photoetching is performed by employing the optical mask containing the target patterns as a mask after the optical proximity correction. The optical proximity correction method disclosed by the invention is simultaneously compatible with corrected image quality and relatively rapid implementation speed.

Description

technical field [0001] The invention relates to the field of optical proximity correction, in particular to an optical proximity correction method based on a neural network model. Background technique [0002] Optical proximity correction (OPC) has become an essential means in the semiconductor manufacturing process. Its purpose is to make the pattern realized on the chip as consistent as possible with the target pattern of lithography through photolithography mask pattern correction. OPC is composed of several key steps, such as target pattern setting in lithography, auxiliary pattern generation and main pattern correction. Due to the deviation caused by etching or the requirements of the lithography process window, the target pattern of lithography is often different from the original design pattern. Auxiliary patterns are lithography process windows used to improve sparse design patterns, and their placement rules are often derived from lithography simulations. The mai...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): G03F1/36
CPCG03F1/36
Inventor 时雪龙赵宇航陈寿面李铭
Owner SHANGHAI INTEGRATED CIRCUIT RES & DEV CENT
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com