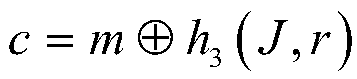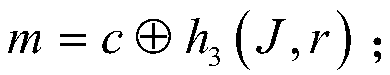Blind signcryption method of elliptic curves in certificateless environments
An elliptic curve, certificate-free technology, applied in the field of cryptography, can solve problems such as high calculation costs
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
Image
Examples
Embodiment 1
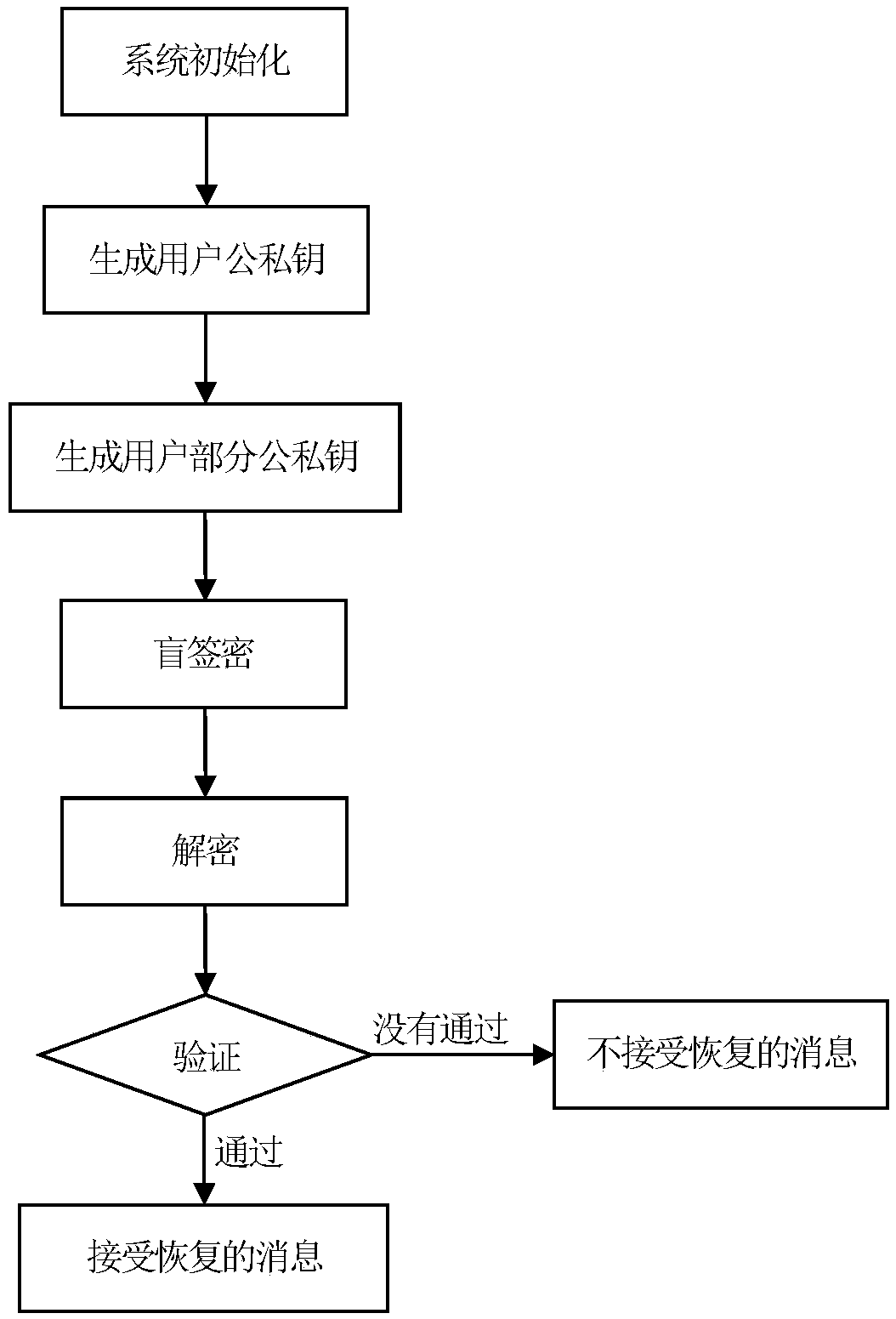
[0077] In this embodiment, the elliptic curve y 2 ≡x 3 +ax+bmodp, large prime number p is 2 192 -2 64 -1 as an example, the elliptic curve blind signcryption method in a certificate-free environment consists of the following steps:
[0078] A. System initialization
[0079] (A1) The key generation center chooses a large prime number p, where p is 2 192 -2 64 -1, define a finite field F p Elliptic curve E on :y 2 ≡x 3 +ax+b, where a,b∈F p is satisfied with 4a 3 +27b 2 ≠0 constant, choose a base point G on the elliptic curve E with order n, E(a,b) and infinite point O form an additive cyclic group G p , G is the additive cyclic group G p A generator of , n is a positive integer whose prime number is finite.
[0080] (A2) The key generation center selects a cryptographically secure Hash function h 1 , Hash function h 2 , Hash function h 3 : Hash function h 1 is {0,1} t ×G p → Z p , Hash function h 2 is {0,1} l ×G p → Z p , Hash function h 3 is G p ×G p ...
Embodiment 2
[0145] In this embodiment, the elliptic curve y 2 ≡x 3 +ax+bmodp, large prime number p is 2 224 -2 96 +1 as an example, the elliptic curve blind signcryption method in a certificate-free environment consists of the following steps:
[0146] A. System initialization
[0147] (A1) The key generation center chooses a large prime number p, where p is 2 224 -2 96 +1, for defining a finite field F p Elliptic curve E on :y 2 ≡x 3 +ax+b, where a,b∈F p is satisfied with 4a 3 +27b 2 ≠0 constant, choose a base point G on the elliptic curve E with order n, E(a,b) and infinite point O form an additive cyclic group G p , G is the additive cyclic group G p A generator of , n is a positive integer whose prime number is finite.
[0148] (A2) The key generation center selects a cryptographically secure Hash function h 1 , Hash function h 2 , Hash function h 3 : Hash function h 1 is {0,1} t ×G p → Z p , Hash function h 2 is {0,1} l ×G p → Z p , Hash function h 3 is G p ...
Embodiment 3
[0156] In this embodiment, the elliptic curve y 2 ≡x 3 +ax+bmodp, large prime number p is 2 256 -2 224 +2 192 +2 96 +1 as an example, the elliptic curve blind signcryption method in a certificate-free environment consists of the following steps:
[0157] A. System initialization
[0158] (A1) The key generation center chooses a large prime number p, where p is 2 256 -2 224 +2 192 +2 96 +1, for defining a finite field F p Elliptic curve E on :y 2 ≡x 3 +ax+b, where a,b∈F p is satisfied with 4a 3 +27b 2 ≠0 constant, choose a base point G on the elliptic curve E with order n, E(a,b) and infinite point O form an additive cyclic group G p , G is the additive cyclic group G p A generator of , n is a positive integer whose prime number is finite.
[0159] (A2) The key generation center selects a cryptographically secure Hash function h 1 , Hash function h 2 , Hash function h 3 : Hash function h 1 is {0,1} t ×G p → Z p , Hash function h 2 is {0,1} l ×G p → Z ...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com