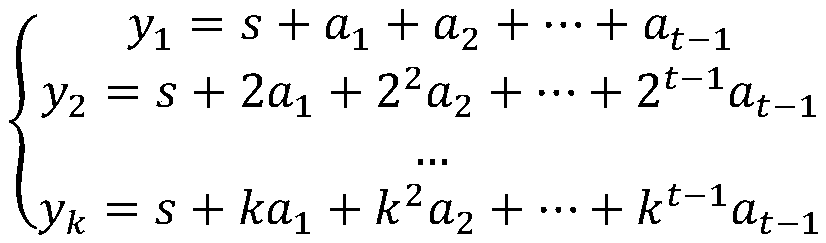Blockchain key sharing and dynamic updating method based on an elliptic curve

An elliptic curve and key sharing technology, which is applied to the public key and key distribution of secure communication, can solve the problems of node master key leakage, and does not support subkey dynamic addition and deletion of master keys, etc., to ensure security, The effect of enhancing trust and strengthening the degree of fit

Inactive Publication Date: 2019-05-17
HANGZHOU QULIAN TECH CO LTD
View PDF3 Cites 7 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

However, in some scenarios, each blockchain node needs to share some data. For data security, the blockchain node will choose to encrypt and store the data, but at this time, who keeps the key pair used for encryption and decryption has become a new the puzzle
The

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Blockchain key sharing and dynamic updating method based on an elliptic curve
  • Blockchain key sharing and dynamic updating method based on an elliptic curve
  • Blockchain key sharing and dynamic updating method based on an elliptic curve

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

[0043] The logic that each step of the present invention executes is as follows:

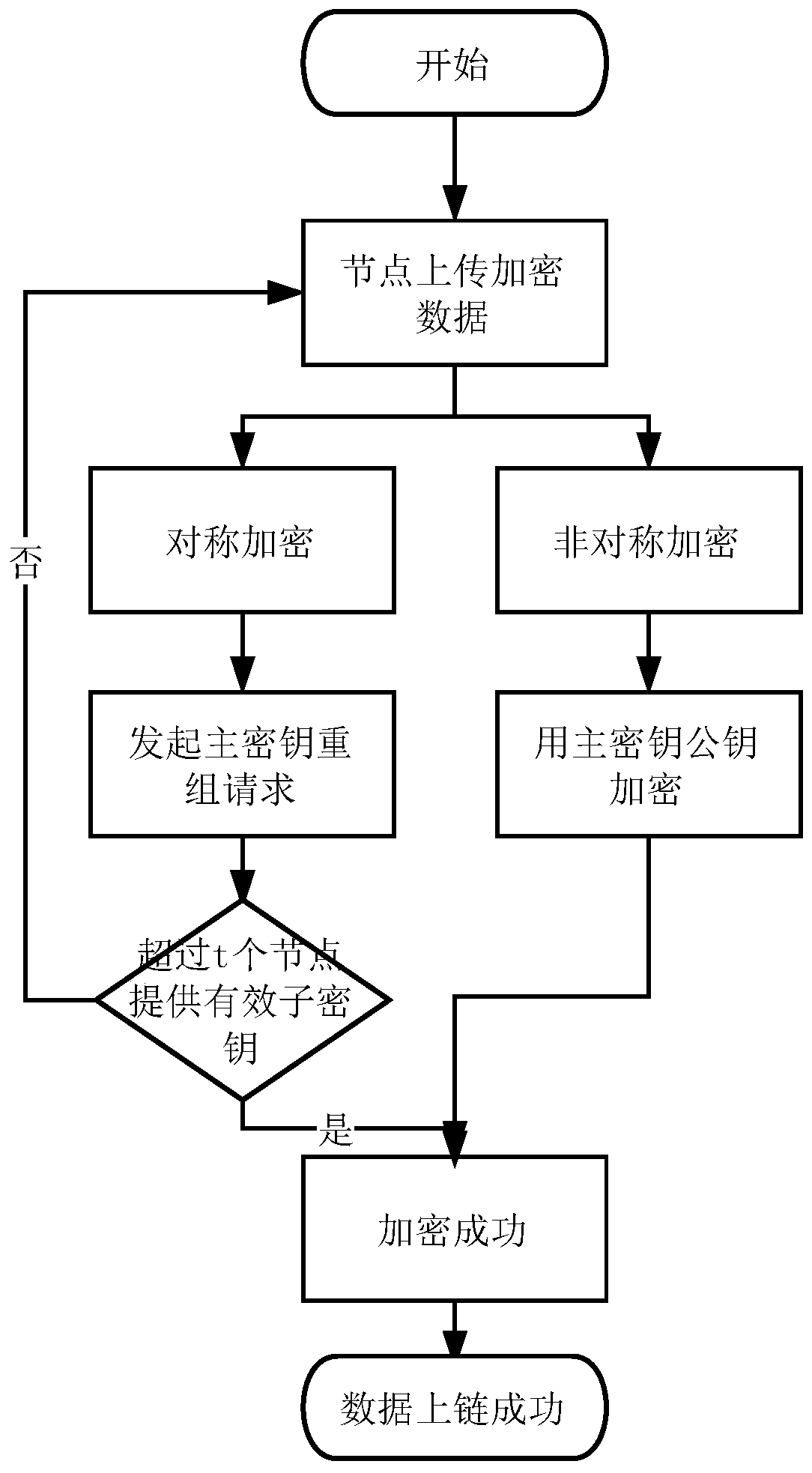
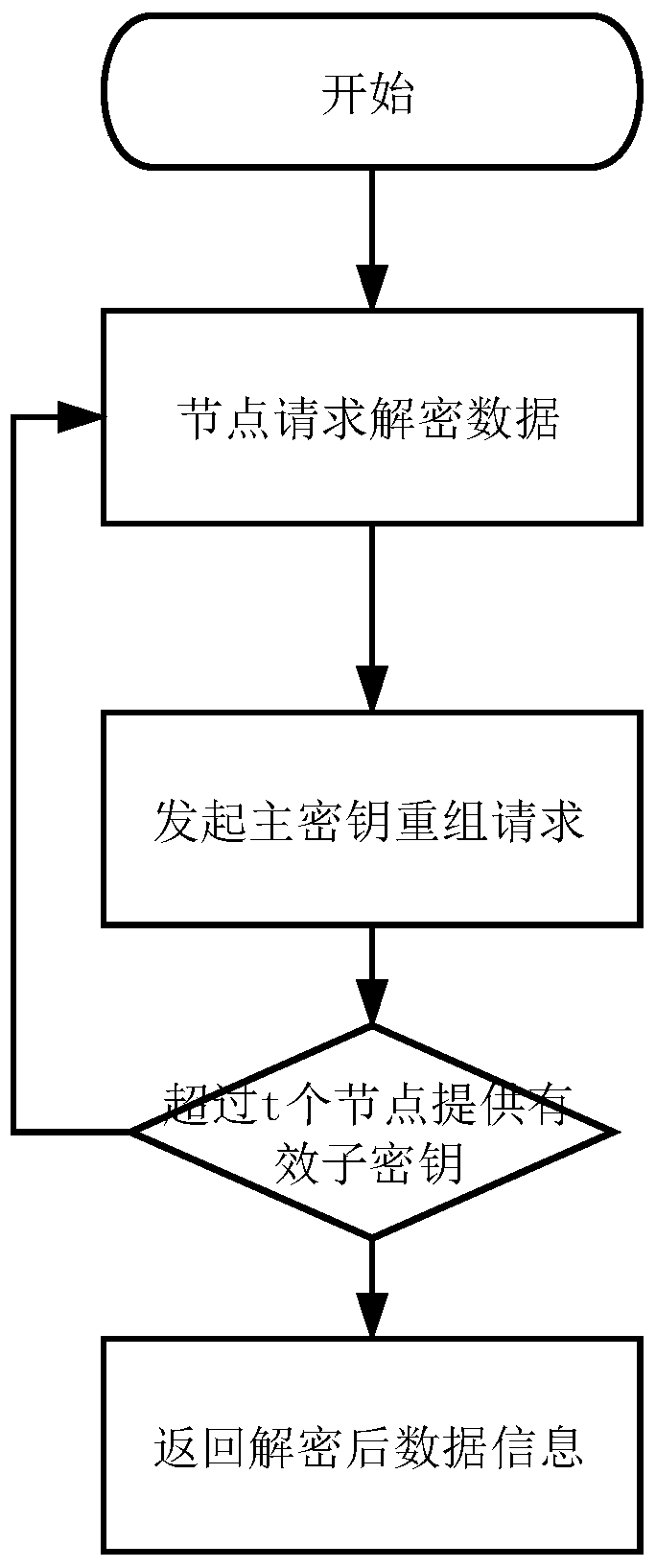
[0044] Node key initialization. When the blockchain runs for the first time, the key initialization contract method is executed in the blockchain environment to initialize the master key and subkey. The contract first randomly generates a master key S, and selects an elliptic curve equation E(a, b) on the prime number field GF, namely: y 2 =x 3 +ax+b, q>3, where 4a 3 -27b 2 ≠0,. The program randomly selects n different parameters on the elliptic curve, denoted as k 1 , k 2 ,…k n As the key of the child node, it is distributed to each node N through a secure channel i . Then, the program selects a base point G on the elliptic curve. Next, the program selects a polynomial of degree t-1 where f(0)=a 0 =S. For j = 1, 2, ... t-1, calculate A j =a j G(mod n), for i=1, 2, ... n, calculate D i =(i,y i )-k i G, and F i =H(k i G), where H(x) is a hash operation method. Then expose E,...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to view more

PUM

No PUM Login to view more

Abstract

The invention discloses a blockchain key sharing and dynamic updating method based on an elliptic curve. The method comprises the steps of node key initialization, sub-key verification, main key synthesis, main key updating, sub-key addition and deletion and data encryption and decryption. Based on the idea of a threshold key sharing system, a linear equation set key sharing technology is proposedto distribute a block chain master key to each node, and the method can dynamically change the master key and add and delete the sub-keys on the premise of not changing node sub-keys, and is matchedwith a scene that the nodes in the block chain network are dynamically added and deleted. The purpose of the invention is to prevent fraud between nodes. According to the method, the sub-keys are distributed, an elliptic curve cryptosystem is combined, the method capable of identifying the authenticity of the sub-keys is also provided after the sub-keys are distributed, the trust problem between the nodes is guaranteed, the security of private data storage of the block chain is guaranteed, the credibility of the block chain system is enhanced, and related operations are defined in the smart contract and cannot be tampered.

Description

technical field [0001] The present invention relates to an elliptic curve cryptosystem, a shared key technology, and a block chain technology, in particular to a block chain key sharing and dynamic update method based on an elliptic curve. Background technique [0002] Elliptic curve cryptography is a public key encryption algorithm based on elliptic curve mathematics. The elliptic curve equation can be expressed as: y 2 =x 3 +ax+b, q>3. of which 4a 3 -27b 2 ≠0, a, b belong to finite field GF(q), q is a prime number or 2 m an integer of . There is a discrete logarithm problem on the elliptic curve, that is, for points K and G on the elliptic curve, satisfying K=kG, it is relatively easy to calculate K for a given k and G, but it is very difficult to solve k according to K and G, The operation performed by k and G here is the scalar multiplication on the finite field. It is precisely because of this characteristic that this difficult problem is applied in cryptograp...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to view more

Application Information

Patent Timeline
no application Login to view more
IPC IPC(8): H04L9/30H04L9/08G06Q20/38
Inventor 邱炜伟李启雷李伟梁秀波尹可挺金鹏
Owner HANGZHOU QULIAN TECH CO LTD
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Try Eureka
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap