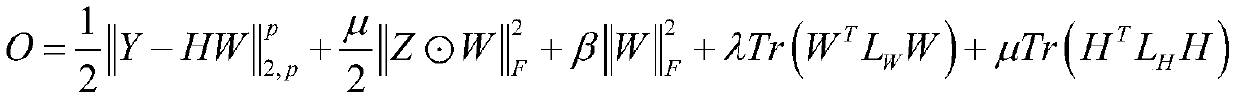A non-negative matrix factorization clustering method for a robust structure based on graph regularization
A technology of non-negative matrix decomposition and clustering method, applied in the field of non-negative matrix decomposition and clustering based on graph regularization, can solve problems such as affecting the discovery of block diagonal structure and reducing performance, and achieve the effect of improving efficiency and accuracy.
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
Image
Examples
Embodiment Construction
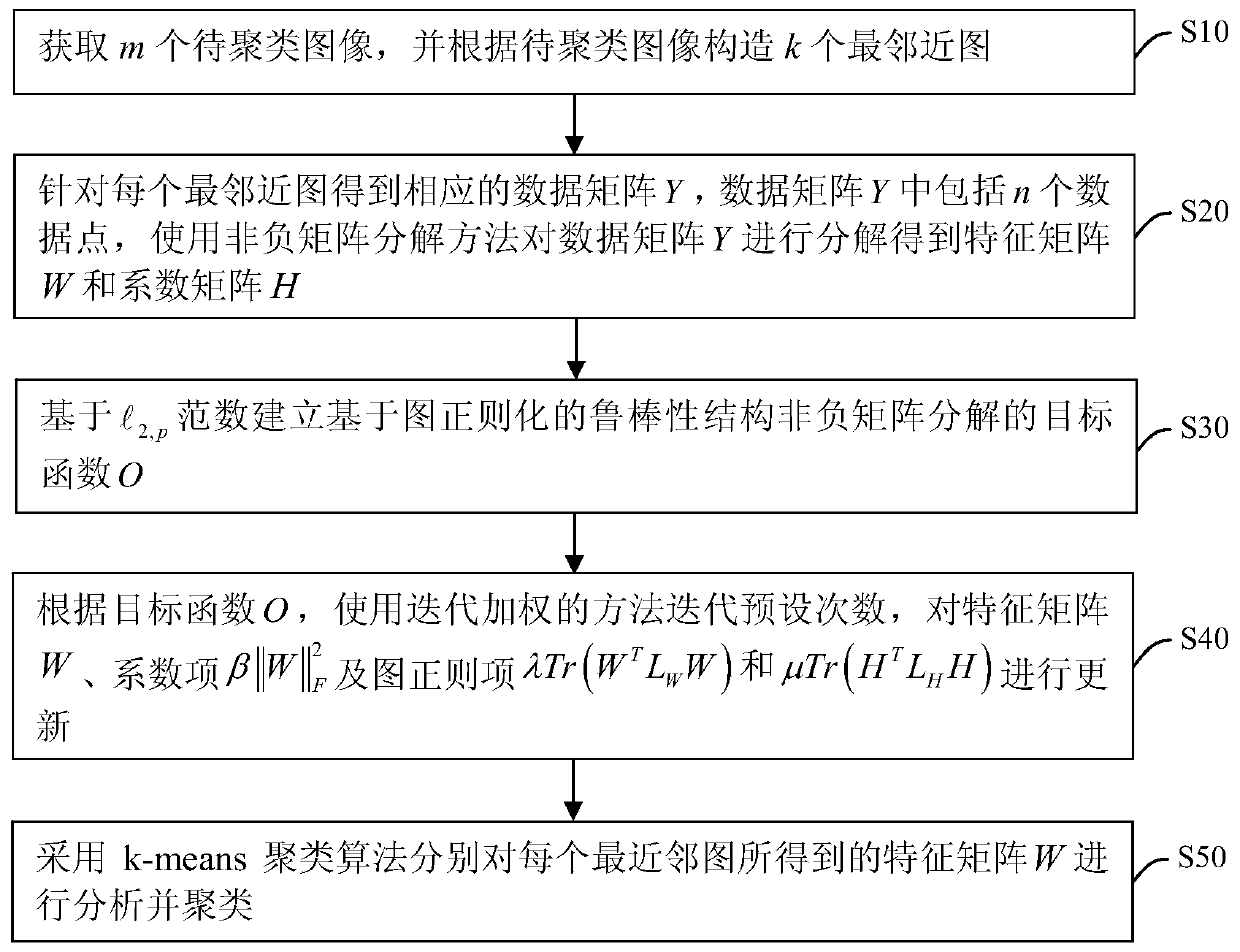
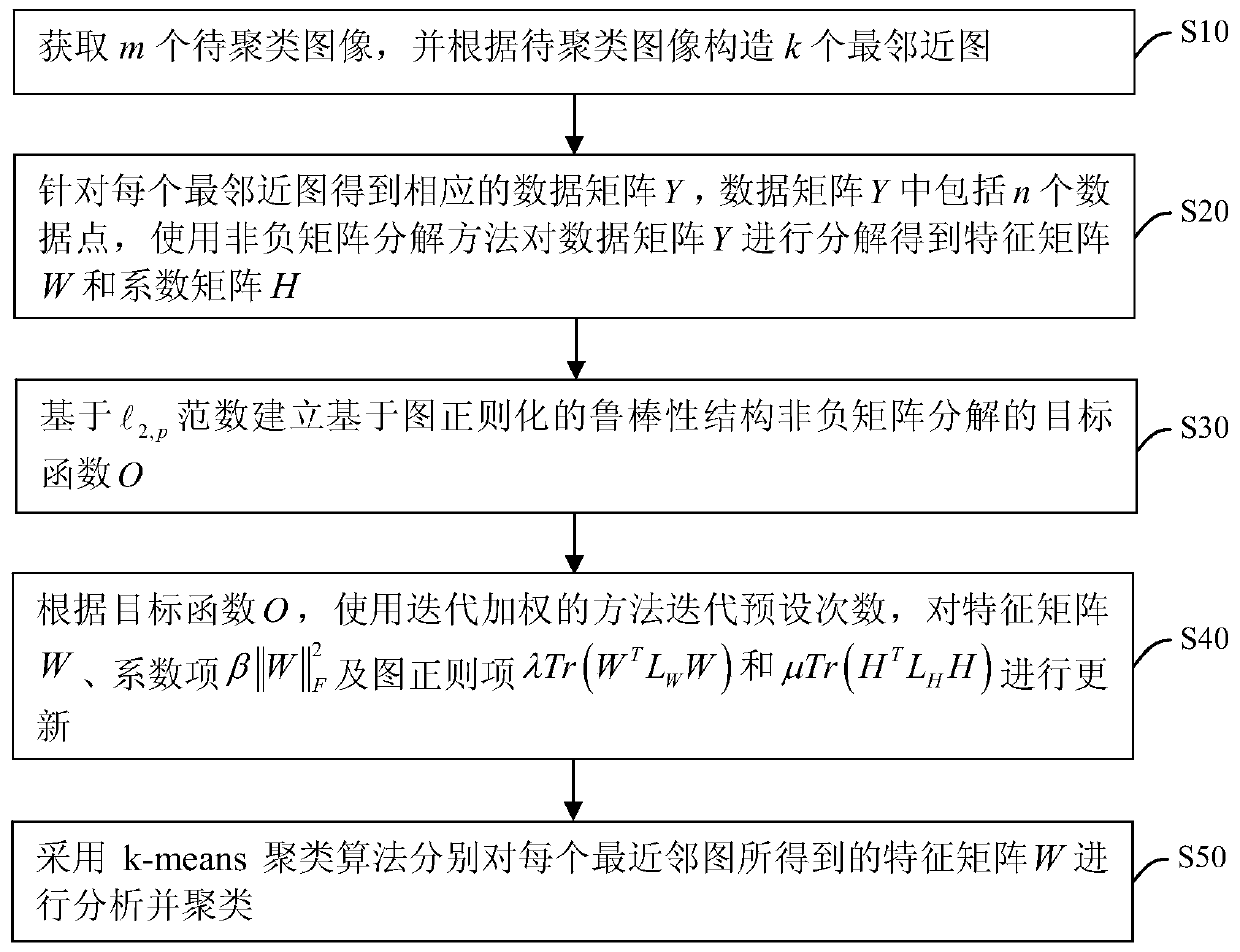
[0017] In order to more clearly illustrate the embodiments of the present invention or the technical solutions in the prior art, the specific implementation manners of the present invention will be described below with reference to the accompanying drawings. Obviously, the accompanying drawings in the following description are only some embodiments of the present invention, and those skilled in the art can obtain other accompanying drawings based on these drawings and obtain other implementations.
[0018] For any matrix B, b i represents the ith row vector of matrix B, b i Represented as the ith column vector of matrix B. If matrix B is a square matrix, use Tr[B] to represent the trajectory of matrix B, and the transpose matrix of matrix B is expressed as B T . When p>0, define the vector b∈R m of The norm is Matrix B ∈ R m×n The Frobenius norm of is Matrix B The norm is
[0019]
[0020] Mix when 0 The (q=2) norm is not a valid matrix norm, so it does not r...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com