Electric power system transient stability calculation method based on semi-implicit Runge-Kutta method

A Runge-Kutta method and power system technology, which is applied in the field of transient stability calculation of power systems based on semi-implicit Runge-Kutta method, which can solve the problems of difficult transient stability simulation of rigid systems, poor numerical stability, and computational speed. Slow and other problems, to achieve the effect of efficient, accurate and stable calculation, good numerical stability, and fast calculation efficiency

Pending Publication Date: 2019-08-16
SOUTHEAST UNIV
View PDF5 Cites 15 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

These integration algorithms have their own unique advantages, but also have different defects. For example, the explicit integration algorithm is simple to calculate and has high calculation efficiency, but its numerical stability is poor, and it does not have A-stability, and its simulation step size is greatly limited by stability. , it is also difficult to apply to the transient stability simulation of rigid systems; the implicit integral algorithm has good numerical stability and has A-stability, but iterative calculation is required, the calculation i...

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Electric power system transient stability calculation method based on semi-implicit Runge-Kutta method
  • Electric power system transient stability calculation method based on semi-implicit Runge-Kutta method
  • Electric power system transient stability calculation method based on semi-implicit Runge-Kutta method

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

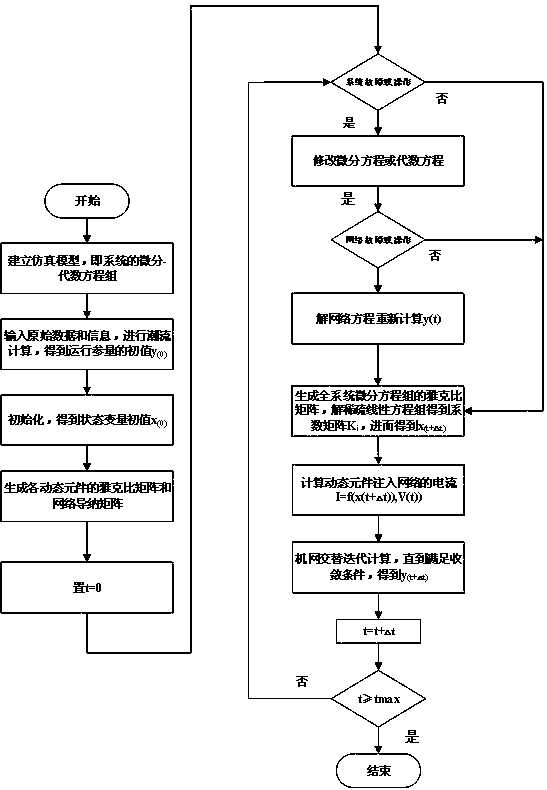
[0052] Power system transient stability calculation method based on semi-implicit Runge-Kutta method, such as figure 1 Shown:

[0053] S1. Establish dynamic component models required for power system transient stability simulation calculation, including generator model, exciter model, PSS model, prime mover model, load model, etc.;

[0054] The system differential equations and algebraic equations are formed to form the whole system dynamic simulation mathematical model, which is described by the differential algebraic equations shown in the following formula:

[0055]

[0056] Among them, x is the state variable describing the characteristics of the dynamic element, and y is the operating parameter of the system in the algebraic equations;

[0057] S2, input raw data and information, perform power flow calculation, and obtain the initial value y of the operating parameter before the system is disturbed (0) , Including the voltage of each node of the system And the power injected int...

Embodiment 2

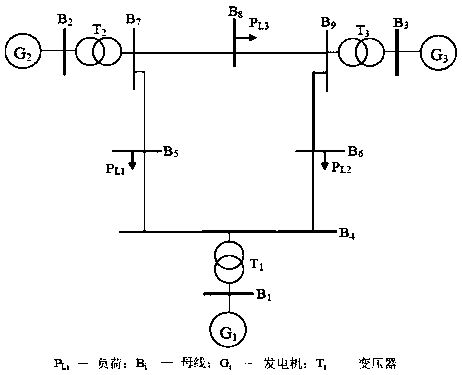
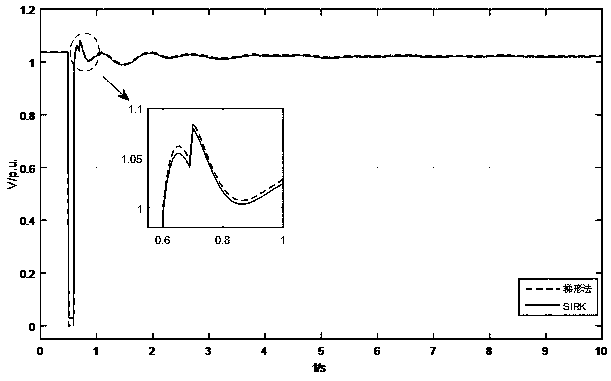
[0089] Take the 3-machine 9-node power system as an example, the single-line structure diagram is as follows figure 2 As shown, there are 3 generators, 3 loads, and 9 branches in the system. The generator adopts the classic second-order model, the load is simulated by constant impedance, the power network is described by the admittance matrix, and the differential equation is described by the second-order three The first-order semi-implicit Runge-Kutta method is used to solve the network equations using the direct method. The entire transient stability calculation process using the above model is as follows:

[0090] Establish a dynamic model to form a system of differential-algebraic equations. The dynamic element model in the system is only a generator, and its classic second-order generator model is

[0091]

[0092] Where T J Is the rotor moment of inertia, D is the damping coefficient

[0093] The system of differential-algebraic equations is as follows:

[0094]

[0095] Among...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to view more

PUM

No PUM Login to view more

Abstract

The invention discloses an electric power system transient stability calculation method based on a semi-implicit Runge-Kutta method. The method includes: establishing a dynamic element model for transient stability simulation calculation of the power system; forming a whole system differential algebraic equation set; inputting raw data and information, carrying out tide calculation, obtaining an operation parameter initial value before system disturbance; calculating an initial value of the state variable; generating a Jacobian matrix and a network admittance matrix of each dynamic element; performing system disturbance judgment; generating a Jacobian matrix of the differential equation set of the whole system; solving and obtaining the value of each state variable at the next moment; carrying out machine network alternate iterative computation, obtaining an operation parameter value at the next moment until a convergence condition is met, and taking the operation parameter value as aninitial value to calculate the next step length. The calculation is simple and stable, the larger step length can be used, the problem that the numerical stability and the calculation efficiency of the algorithm are difficult to consider at the same time in the transient stability simulation calculation is solved, and the method is more efficient, accurate and stable.

Description

[0001] Field [0002] The invention belongs to the technical field of power system transient stability simulation and analysis, and specifically relates to a power system transient stability calculation method based on a semi-implicit Runge-Kutta method. Background technique [0003] With the development of smart grids and AC / DC hybrid grids, the operation of the power system has become more complex and changeable. Power systems often suffer from different levels of faults and disturbances. In order to ensure the continuous safe and stable operation of the power system, it is necessary to judge in advance whether the power system can operate stably under different fault disturbances. Therefore, transient stability simulation and analysis are required. Transient stability analysis generally refers to the electromechanical transient process after the system is subject to large disturbances. The duration is a few seconds to ten seconds. The rapid and accurate transient stability simul...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to view more

Application Information

Patent Timeline
no application Login to view more
IPC IPC(8): G06F17/50G06F17/13
CPCG06F17/13G06F30/20
Inventor 顾伟刘伟琦柳伟李培鑫史文博
Owner SOUTHEAST UNIV
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Try Eureka
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap