Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Star map identification method for precise tracking telescope

A technology of star map recognition and recognition method, which is applied in the field of star map recognition, can solve problems such as cumulative error, unsuitable large field of view, slow matching speed, etc., and achieve the effects of speeding up, increasing universality, and reducing storage space

Pending Publication Date: 2020-03-17
中国科学院国家天文台长春人造卫星观测站
View PDF13 Cites 2 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0003] In order to solve the problems of the existing star map matching method, such as slow matching speed, inapplicability to large field of view and dynamic tracking, and cumulative errors in a relatively large dynamic observation range, the present invention provides a star map used for precision tracking telescopes. graph recognition method

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Star map identification method for precise tracking telescope
  • Star map identification method for precise tracking telescope
  • Star map identification method for precise tracking telescope

Examples

Experimental program
Comparison scheme
Effect test

specific Embodiment approach 1

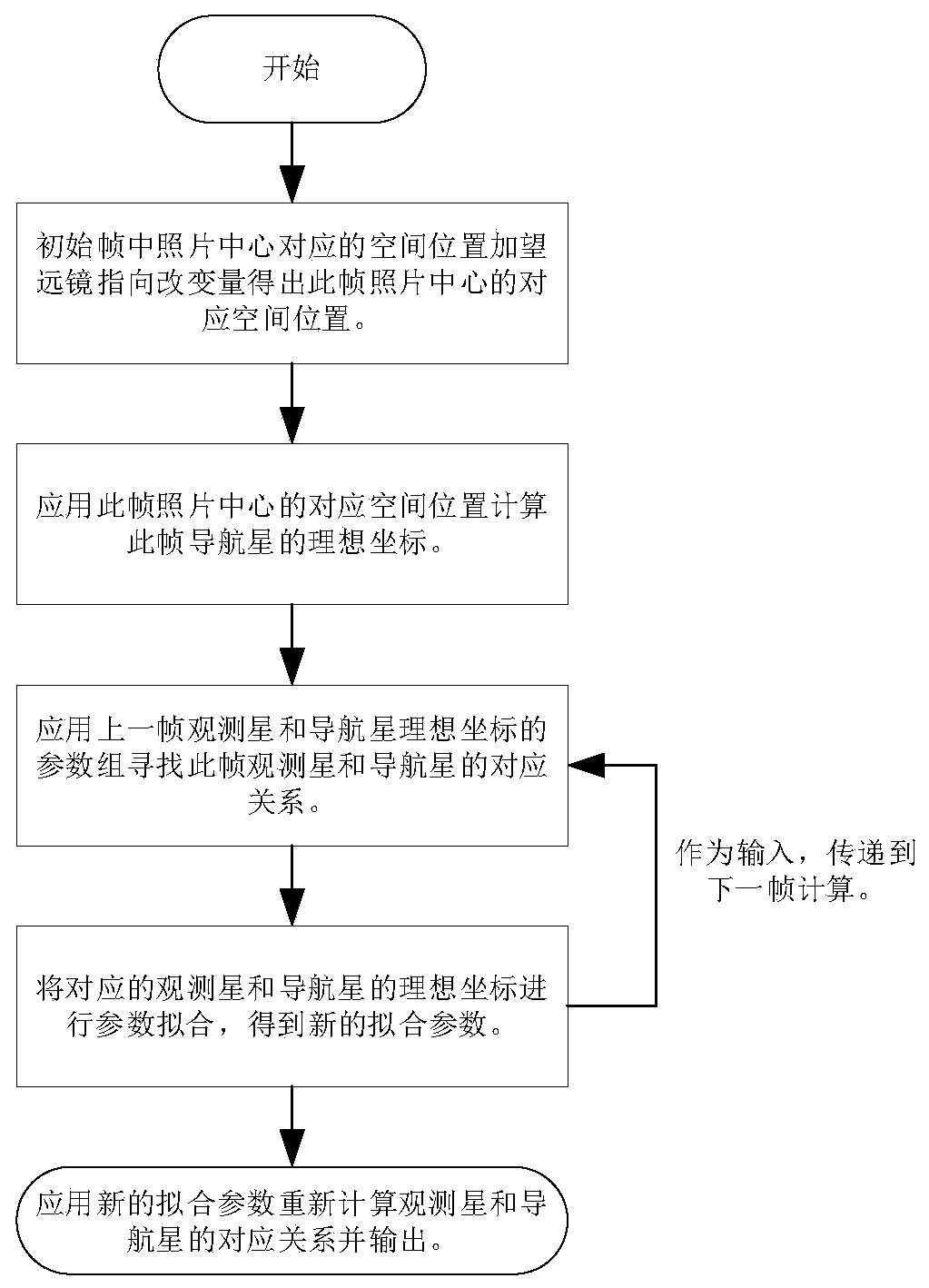
[0034] Specific implementation mode 1. Combination Figure 1 to Figure 3 Describe this embodiment, a star map recognition method for precision tracking telescopes, including two parts: the first frame recognition method and the continuous frame refresh method.

[0035] The spatial position corresponding to the midpoint of the photo obtained by the first frame recognition method and the initial corresponding fitting parameters are used as the input of the continuous frame refresh algorithm. Among them: the position corresponding to the midpoint of the first frame plus the amount of change in each frame of the telescope relative to the position of the first frame is used as a parameter for subsequent calculation of the ideal coordinates of the navigation star; the initial corresponding fitting parameters are used to obtain the first fitting corresponding relationship in the second frame , and then this relationship is fitted and refreshed, and the fitting parameters are output a...

specific Embodiment approach 2

[0076]Specific embodiment two, present embodiment is the embodiment of a kind of star map identification method that is used for precision tracking type telescope described in specific embodiment one:

[0077] Telescope platform: Changchun Satellite Observatory 1.2-m telescope.

[0078] Observation time: April 21, 2019

[0079] The telescope points to the sky area: (Ra: 9.318417h–9.402894h), (Dec: 0.392261°–0.069461°)

[0080] Data composition: a total of 30 frames of data, the number of observation stars per frame: 360-616, the number of navigation stars per frame: 19-27.

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a star map identification method for a precise tracking telescope, relates to the technical field of star map identification, and solves problems that a star map matching method in the prior art is low in matching speed and not suitable for large-view-field and dynamic tracking, and accumulated errors exist in a large dynamic observation range. The method comprises a firstframe identification method and a continuous frame refreshing method. The star map identification method is characterized in that accuracy and real-time performance in star map identification application of a precision tracking telescope are fully considered, the experience requirement of error selection is reduced; the priori information such as telescope pointing and rotation is not needed, compared with a traditional triangle matching algorithm, the storage space is reduced. The rapid, precise and stable star map identification is provided for a precision tracking telescope, and the methodis suitable for automatic target identification of the precision tracking telescope. The star map identification technology is divided into two algorithms which can be operated independently so as tomeet different application occasions.

Description

technical field [0001] The invention relates to the technical field of star pattern recognition, in particular to a star pattern recognition method for precision tracking telescopes. The invention is suitable for automatic target recognition of precision tracking telescopes. The star map recognition technology is divided into two algorithms that can operate independently to meet different application occasions. Background technique [0002] Star map matching is an important link in the research of astronomical stargazing and space navigation. Through the observation of stars by optical telescopes or star sensors, the observation position is identified, and then information such as the position, orbit and attitude of the target or itself is inferred. Star map matching can be generally divided into two methods, one is to do geometric matching by observing the relative positional relationship between the stars and the navigation stars in the star library. The commonly used m...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): G01C21/02G01C21/20
CPCG01C21/025G01C21/20
Inventor 刘德龙杨文波李振伟
Owner 中国科学院国家天文台长春人造卫星观测站
Features
  • Generate Ideas
  • Intellectual Property
  • Life Sciences
  • Materials
  • Tech Scout
Why Patsnap Eureka
  • Unparalleled Data Quality
  • Higher Quality Content
  • 60% Fewer Hallucinations
Social media
Patsnap Eureka Blog
Learn More

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com